6. Метричні задачі

При розробці технічних креслень дуже часто доводиться розв’язувати метричні задачі, які пов’язані з вимірюванням різних параметрів геометричних образів.

Умовно ці задачі можна об’єднати у три групи:

1. Вимірювання довжин і відстаней:

2. Визначення дійсних величин плоских фігур і перерізів:

3. Вимірювання кутів.

Метричні задачі доцільно розв’язувати за допомогою розглянутих вище способів перетворення проекцій.

6.13. Визначення кута між прямою і площиною

К утом між прямою m і площиною T (рис. 6.16) називається гострий кут , утворений цією прямою з її проекцією на дану площину. Побудова проекцій кута вимагає визначення двох точок K і L, перша із яких є точкою перетину даної прямої з площиною , а друга – основою перпендикуляра, опущеного із довільної точки А прямої на ту ж площину. Здобувши дві прямі, що перетинаються в точці К (прямі m і l), визначаємо дійсну величину кута між ними способом, розглянутим вище.

П одібний хід розв'язання задачі, хоча й є логічним, але він достатньо складний для виконання на комплексному кресленні. Цю задачу доцільно розв’язувати за допомогою так званого "додаткового" кута. Дійсно, з розгляду рис. 6.16 випливає, що трикутник ALK прямокутний. Тому сума кутів і дорівнює . Якщо будь-яким відомим нам способом визначити дійсну величину кута між прямою m і перпендикуляром n до площини Т, то додатковий до кут, який дорівнює , буде шуканим кутом між прямою m та площиною Т.

Розв'яжемо цю задачу на комплексному кресленні (рис. 6.17). Визначимо величину кута між прямою а і площиною , яку задано двома паралельними прямими b i c. Для розв’язання цієї задачі застосуємо метод "додаткового" кута.

Із довільної точки К прямої а опускаємо перпендикуляр n на площину , для чого в цій площині проводимо її горизонталь h і фронталь f. Далі обертанням навколо прямої рівня (наприклад, горизонталі ) визначаємо натуральну величину кута між заданою прямою а і перпендикуляром n до площини . Знаходимо нове положення точки К і з’єднуємо його з нерухомими точками 1 і 2 на осі обертання , отримуємо натуральну величину кута . Будуємо додатковий до кут . Цей кут і буде кутом між прямою а і площиною .

6.14. Визначення кута між площинами

Мірою кута між двома площинами є лінійний кут, утворений двома прямими, які є перерізами граней цього кута площиною, перпендикулярною до їх спільного ребра. Для знаходження лінійного кута необхідно виконати такі геометричні побудови (рис. 6.18):

1. Визначити у просторі пряму а, яка є лінією перетину двох заданих площин і .

2. Провести нову площину 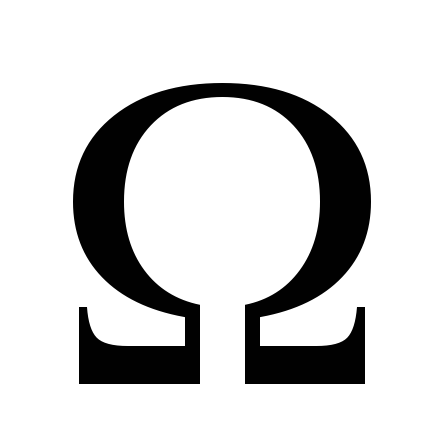, перпендикулярну до прямої а.

3. Побудувати лінії перетину k i l площини з площинами і .

4. З найти величину кута між прямими k i l, який визначає величину кута між площинами і . Якщо цей кут перевищує , то за міру кута між площинами беруть кут додатковий до .

Розглянутий план розв’язання задачі передбачає виконання значної кількості геометричних побудов, які пов’язані з находженням лінії а перетину двох заданих площин, проведенням площини , перпендикулярної до лінії перетину, подвійним розв’язанням задачі по визначенню ліній перетину площин, тобто знаходженню прямих k і l. Тільки після цього можна приступити до знаходження величини кута , який у загальному випадку утворюється прямими загального положення.

П одивимося, як можна спростити розв’язання цієї задачі. Доповнимо рис. 6.18 точкою К, яка належатиме площині , і опустимо з цієї точки перпендикуляри m i n на площини і (рис. 6.19). Точки С і D перетину цих перпендикулярів з площинами сумісно з точками К і В є вершинами плоского чотирикутника КСВD, у якого кути при вершинах С і D прямі. Отже, між кутами і існує залежність . З рис. 6.19 випливає, що замість кута значно простіше знаходити кут , додатковий до .Тобто й у цьому випадку доцільно застосовувати спосіб "додаткового" кута.

Приклад розв’язання подібної задачі подано на рис. 6.20, на якому площини задані головними своїми лініями. Для визначення кута між цими площинами із довільної точки К простору до них проведені два перпендикуляри n i . Далі задача зводиться до визначення кута між двома прямими n i , що перетинаються. У нашому прикладі її розв’язано способом обертання навколо прямої рівня. Оскільки кут гострий, то він є мірою шуканого кута між цими площинами і, отже, немає потреби шукати додатковий до кут.

Визначення кута між двома площинами значно спрощується, якщо площини задані таким чином, що на комплексному кресленні присутня лінія їх перетину. Тобто дві площини явно утворюють двограний кут (рис. 6.21). У цьому випадку розв’язання задачі зводиться до перетворення лінії АВ, яка є прямою загального положення, у проекціювальну пряму, що можливе послідовним виконанням першої та другої основних задач. Обидві площини при цьому також займуть положення проекціювальних площин.

На рис. 6.21 задача розв’язана способом заміни площин проекцій. Після першої заміни відрізок АВ – спільне ребро двограного кута – зайняв положення прямої рівня. Це є результатом того, що нова вісь проекцій була розташована паралельно горизонтальній проекції ребра.

Після другої заміни площин проекцій, коли площина була замінена площиною , відрізок АВ перетворився у проекціювальнну пряму. Нова вісь проекцій перпендикулярна до проекції відрізка АВ. Кут між проекціями-прямими площин є шуканим кутом між заданими площинами.

На завершення відзначимо, що розглянуті вище метричні задачі, більшість з яких доцільно розв’язувати із застосуванням способів перетворення комплексного креслення, дуже часто входять складовою частиною до різноманітних конструктивних задач, які на практиці доводиться розв'язувати при розробці тих чи інших технічних проектів. Тому оволодіння методами їх розв’язання має дуже важливе практичне значення.

29