Транспортная задача с целевой функцией на минимизацию стоимости доставки

Данный тип задач обеспечивает решение целого класса экономических задач совсем обязательно связанных с перевозками, например задача севресного обслуживания решается по этому же типу.

Математическая модель задачи:

1. Условие - имеется m источников (товара) А₁, А₂,…А_m

2. В каждом из этих источников имеется определенное количество товаров а₁, а₂,…а_m

3. Имеется определенное количество n-потребителей (товаров) В₁,В₂….В_m

4. И определить количество заказов в₁, в₂,….в_n

5. Для того чтобы описать затраты на перевозку описываемой матрици затрат на доставку, матрица записывается в виде А_i,B_j->C_ij

Таблица 13

	A1	A2	A3
B1	C11	C21	C31
B2	C21	C22	C32
B3	C31	C23	C35

Типовая ЦФ формируется следующим образом. Составляется план перевозок из пунктов поставки А₁- А_m, ,и В1-В_mудовлетворяет заказ в₁ - в_nпри минимальных затратах C_ij->min.

При этом объем перевозок по каждому направлению обозначается через Х большое. Х_ij–объем перевозок.

Задачи бывают двух типов: открытая и закрытая, если сумма заказа равна сумме запасов – закрытая, если меньше-открытая, больше- задача не имеет решения.

Математический вид модели

ЦФ= L(x)=*->min

Ограничение:

=

Решение-неотрицательное

≥0 i=ij=

Решением является матрица оптимальныхперевозок

=()m*n Алгоритм решения:

1. Формируем исходные опорные решения задачи;

2. Проведем решение на оптимальность, или критерий оптимальности не выполняет формирование следующего решения, которое в свою очередь также проверяется на оптимизацию такой тип решения нерациональным.

Общий вид распределительной таблицы

bj ai		1	2	…	j	…	n
				…		…
1		C11 X11	C12 X12	…	C1j X1j	…	C1n X1n
2		C21 X21	C22 X22	…	C2j X2j	…	C2n X2n
3		Ci1 Xi1	Ci2 Xi2	…	Cij Xij	…	Cin Xin
m		Cm1 Xm1	Cm2 Xm2	…	Cmi xmi	…

При создании таблицы с исходным опорным решением значения хне заданы, остальные значения в условиях.

Для первоначального заполнения значений существует несколко методов, один из которых-метод минимального тарифа его смысыл в первую очередь объем перевозимых грузов вписываем в клетку с минимальным тарифом.

Для того чтобы можно было применить симплекс метод матрица должна удовлетворять условие новорожденности .

Которое формулируется следующим образом

-число клеток где >0 должно быть больше или равно m+n-1, поэтому после заполнения первоначальных значений

Пример :

Склады: А₁, А_2,А₃

Запасы а₁=90

а₂= 400

а₃=110

потребители В₁,В₂,В₃

заказы в₁=140

в₂=300

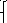
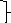в₃=160

Матрица стоимости перевозок = 2 5 2

4 1 5

b a		1	2	3
		140	300	160
1		2 90	5	2
2		4	1 300	5 100
3		3 50	6	8 60

=90+400+110=600

=140+300+160=600

>0 должно быть

3+8-1

≥5-матрица не вырождена

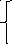
90 0 0

0. 300 100

50. 0 60

L() =(90*2+300*1+100*5+50*3+60*8)=1610

Проверка решения на оптимальность проводится методом потенциалов.

+-удовлетворяет условие

++-+=0-для занятых клеток

++-≤0-для свободных

и -потенциалы

Для того чтобы рассчитать уровень потенциала добовляем еще одну строку в столбце.

Следующим этапом строится прямоугольный потенциал, он строится так что одна его вершина строится в пустой клетке а остальные три через занятые клетки. Т адиагональ которая начинается от пустой клети маркируется значком «+» а диагональ по порядку «-» и «+».Выписываем значения меньше по размеру «-» вычитаем от «-» и прибавляем к «+».

0+60=60; 90-60=30; 50+60=110; 60-60=0На основании новых значений грузопотока в вершине заменив новую матрицу

L()=2*30+5*0+2*60+0*4+300*1+5*100+3*110+0*6+0*8=1310

3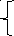0 0 60

0 300 100

110 0 0

b a			1	2	3
			140(50)0	300(0)	160(60)0
1	0		2 - 90	5 0	2 0 +	0
2	100 0		4 + 0	1 300	5 -100	-2
3	60 0		+ 3 50	6 0	8 60	1
j			2	3	7

b a		1	2	3
		140	300	100
1		2 30-	5 0	2 6+	0
2		4 0 +	1 300	5 100 -	3
3		3 110	6 0	8 0	1
j		2	-2	2

+-=0

=0

+-=0

=

=2

=2

∆1,2=+-=-2 <0

∆1,3=+-=5>0

∆2,1=+-=-4<0

∆3,2=+-=-2<0

30 0 60

0 300 100

110 0 0

b a		1	2	3
		140	300	100
1		2 30 -	5 0	2 6 +	0
2		4 0+	1 300	5 100 -	3
3		3 110	6 0	8 0	1
j		2	-2	2

L()=2*30+5*0+2*60+0*4+300*1+5*100+3*110+0*6+0*8=1310