Программное обеспечение современных ЭВМ

Вычислительные машины

Конспект лекций

Структура курса

Цель курса

Формирование понимания принципов функционирования аппаратного и программного обеспечения современных персональных ЭВМ и вычислительных систем. Приобретение практических навыков работы с техническим и программным обеспечением персональных ЭВМ и вычислительных систем.

Задачи курса

1.Изучение физических основ функционирования ЭВМ;

2.Изучение логических основ построения ЭВМ;

3.Получение знаний по составу аппаратного обеспечения ЭВМ;

4.Изучение принципов построения операционных систем ЭВМ;

5.Приобретение практических навыков сборки ПЭВМ из комплектующих.

Структура учебного плана

•Количество лекционных занятий: 72 академических часа.

•Количество лабораторных занятий: 72 академических часов.

•Количество лабораторных занятий: 36 академических часов.

•Индивидуальная работа: 108 академических часа.

•2 модульные контрольные работы.

•Экзамен.

Литература. Учебные материалы

1.Вычислительные системы, сети и телекоммуникации: Учебник/А.П. Пятибратов, Л.П. Гудынко, А.А. Кириченко; Под. ред. А.П. Пятибратова. - М.: Финансы и статистика, 1998. - 400 с: ил.

2.Информатика: Учебник / Под ред. проф. Н.В. Макаровой. - 2-е изд. - М.: Финансы и статистика, 1998. 768 с., ил.

3.Острейковский В.А., Информатика: Учеб для ВУЗов. - М.: Высш. шк., 1999. - 511 с., ил.

Обновленный список рекомендованной литературы для изучения курса доступен по адресу http://www.edu.cassiopeia.com.ua

Раздел 1. Архитектура вычислительных машин

Лекция 1

Развитие вычислительной техники и ее классификация

1.1. История вычислительной техники.

Вычислительные машины принято делить на поколения. Это деление весьма условно и вызвано стремительным развитием вычислительной техники как в смысле элементной базы, на которой они строятся, так и в смысле изменения их структуры.

Условно к вычислительным машинам нулевого поколения относятся механические компьютеры (1642-1945):

•Механическая счëтная (суммирующая) машина. Блез Паскаль (1623-1662)

•Проект LINGUA GENERALIS. Готфрид Вильгельм Лейбниц (1646-1717)

•Разностная и аналитическая машины, понятие и реализация условного перехода. Чарльз Беббедж (1792-1871)

•Программирование, понятие ячеек памяти, цикла. Ада Августа Лавлейс (18151852)

•Математические методы вычислений. Карл Фридрих Гаусс (1777-1855)

•Суммирующая машина с проверкой вводимых данных и печатью результатов вычислений. Уильям Барроуз (1857-1897)

•Табулятор Холлерита, перфокарты, применение ВМ при проведении статистических исследований. Германн Холлерит (1860-1929)

•Первые релейные ВМ. Цузе (Германия, 1941)

•Программируемая релейная ВМ ‘МАРК-1’ (1944). Говард Гатуэй Айткен

•Первая ламповая ЭВМ ЭНИАК (1945). Д.Моучли-Д.Эккерт

1.2.Архитектура фон Неймана

Оценив ограничения ЭВМ ЭНИАК, Джон фон Нейман (1903-1957) предложил структуру вычислительной системы, построенной на следующих принципах.

1.Основными ее блоками являются арифметико-логическое устройство, устройство управления, запоминающее устройство и устройства ввода-вывода.

2.Программы и данные хранятся в одной и той же памяти.

3.Устройство управления и арифметико-логическое устройство, обычно объединенные в центральный процессор, определяют действия, подлежащие выполнению, путем считывания команд из оперативной памяти.

4.Внутренний код машины двоичен.

Архитектура ЭВМ, построенная в соответствии с этими принципами приведена на рис.1.

Рис.1. Архитектура ЭВМ фон Неймана

Подавляющее большинство вычислительных машин в настоящее время являются фоннеймановскими машинами.

1.3. Развитие архитектуры вычислительных машин

Первое поколение — ламповые машины (1945-1955) с быстродействием порядка 10...20 тысяч операций в секунду. Это сравнительно медленные машины, для которых программы писались большей частью на языке машины.

Основные характеристики машин первого поколения представлены на примере БЭСМ-1 (1953 г.): емкость памяти - 2048 слов, скорость - 7000...8000 операций/сек, разрядность - 39 разрядов; арифметика - двоичная с плавающей запятой; система команд - трехадресная; устройство ввода - перфолента двухдорожечная; объем аппаратуры - около 4000 ламп, внешние ЗУ - барабаны на 5120 слов, магнитная лента - до 120000 слов, вывод на быструю цифровую печать - 300 строк в минуту.

Второе поколение — транзисторные машины (1955-1965) с быстродействием порядка сотен тысяч операций в секунду. Это машины, на которых имелись трансляторы с алгоритмических языков, широкий набор библиотечных программ, расширенные возможности по вводувыводу, увеличенный объем запоминающих устройств, развитые системы программирования.

Для стиля их использования характерен так называемый ‘закрытый режим’, когда программу, обычно записанную на языке высокого уровня, программист отдает в группу обслуживания, которая занимается дальнейшей обработкой его задачи - перфорированием и пропуском на машине.

Третье поколение — машины на интегральных схемах (1965-1980) с быстродействием порядка миллионов операций в секунду. Это семейства программно-преемственных (совместимых) машин с развитой системой прерывания и развитыми операционными системами.

Следует отметить, что многие машины, которые по своей электронике относятся к ЭВМ второго поколения, обладают всеми структурными особенностями, свойственными машинам третьего поколения. В этом смысле деление на поколения достаточно условно.

Четвертое поколение — машины на больших интегральных схемах (БИС) (1980-?), обладающие быстродействием в десятки миллионов операций в одну секунду. Это машины, оснащенные микропроцессором - устройством, изобретенным Тэдом Хоффом (компания

Intel).

Первая версия персональных компьютеров IBM PC была оснащена операционной системой MS-DOS, которую выпускала тогда еще крошечная корпорация Microsoft. IBM и Microsoft совместно разработали последовавшую за MS-DOS операционную систему OS/2, характерной чертой которой был графический интерфейс, сходный с интерфейсом Apple Macintosh. Между тем компания Microsoft также разработала собственную операционную систему Windows, которая работала на основе MS-DOS, на случай, если OS/2 не будет иметь спроса. OS/2 действительно не пользовалась спросом, a Microsoft успешно продолжала выпускать операционную систему Windows, что послужило причиной грандиозного раздора между IBM и Microsoft.

1.4. Основные классы вычислительных машин

Персональные компьютеры (ПК) и рабочие станции. ПК первоначально ориентировались на самого широкого потребителя непрофессионала. Тем не менее быстрый рост производительности ПК на базе новейших микропроцессоров Intel в сочетании с резким снижением цен на эти изделия и развитием технологии локальных шин (VESA и PCI),

позволяющей устранить многие "узкие места" в архитектуре ПК, делают современные персональные компьютеры весьма привлекательной альтернативой рабочим станциям.

Ориентация рабочих станций на профессиональных пользователей привела к тому, что рабочие станции - это хорошо сбалансированные системы, в которых высокое быстродействие сочетается с большим объемом оперативной и внешней памяти, высокопроизводительными внутренними магистралями, высококачественной и быстродействующей графической подсистемой и разнообразными устройствами ввода/вывода. Это свойство выгодно отличает рабочие станции среднего и высокого класса, напимер, UNIX-станции, от ПК и сегодня.

X-терминалы представляют собой комбинацию бездисковых рабочих станций и стандартных ASCII-терминалов. X-терминалы отличаются от ПК и рабочих станций не только тем, что не выполняет функции обычной локальной обработки. Работа X-терминалов зависит от главной (хост) системы, к которой они подключены посредством сети. Для того, чтобы X- терминал мог работать, пользователи должны инсталлировать программное обеспечение многооконного сервера X11 на главном процессоре, выполняющим прикладную задачу (наиболее известная версия X11 Release 5). Х-терминалы отличаются также от стандартных алфавитно-цифровых ASCII и традиционных графических дисплейных терминалов тем, что они могут быть подключены к любой главной системе, которая поддерживает стандарт X- Windows. Более того, локальная вычислительная мощь X-терминала обычно используется для обработки отображения, а не обработки приложений (называемых клиентами), которые выполняются удаленно на главном компьютере (сервере). Вывод такого удаленного приложения просто отображается на экране X-терминала.

Серверы. Прикладные многопользовательские коммерческие бизнес-системы, включающие системы управления базами данных, разработку программного обеспечения и т.д. все более нуждаются в переходе к модели вычислений "клиент-сервер" и распределенной обработке. В распределенной модели "клиент-сервер" часть работы выполняет сервер, а часть пользовательский компьютер.

Современные серверы характеризуются повышенными требованиями к аппаратной части: наличием двух или более центральных процессоров, многоуровневой шинной архитектуры, в которой высокоскоростная системная шина связывает между собой несколько процессоров и оперативную память, а также множество стандартных шин ввода/вывода, размещенных в том же корпусе, поддержкой технологии дисковых массивов RAID и т.д..

Мейнфреймы представляют собой многопроцессорные системы, содержащие один или несколько центральных и периферийных процессоров с общей памятью, связанных между собой высокоскоростными магистралями передачи данных. При этом основная вычислительная нагрузка ложится на центральные процессоры, а периферийные процессоры обеспечивают работу с широкой номенклатурой периферийных устройств.

Основными поставщиками мейнфреймов являются известные компьютерные компании

IBM, Amdahl, ICL, Siemens Nixdorf и некоторые другие.

Кластерные архитектуры - объединение машин, представляющееся единым целым для операционной системы, системного программного обеспечения, прикладных программ и пользователей. Машины, кластеризованные вместе таким способом могут при отказе одного процессора очень быстро перераспределить работу на другие процессоры внутри кластера.

Работа любой кластерной системы определяется двумя главными компонентами: высокоскоростным механизмом связи процессоров между собой и системным программным обеспечением, которое обеспечивает клиентам прозрачный доступ к системному сервису.

1.3.4.Вопросы для обсуждения.

1.Каким должен быть коипьютер пятого поколения?

2.Какими преимуществми и недостатками обладают каждая из рассмотренных классов вычислительных систем?

Лекция 2

Системы счисления

2.1. Позиционные системы счисления.

Система счисления — способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами. В зависимости от способа изображения чисел, системы счисления делятся на:

•позиционные;

•непозиционные.

Впозиционной системе счисления количественное значение каждой цифры зависит от

еепозиции в числе. В непозиционной системе счисления цифры не меняют своего количественного значения при изменении их расположения в числе.

Позиционная система счисления задается алфавитом A={a1, a2,… ak} и основанием P≠0. Символы алфавита ai называют цифрами. Каждому символу алфавита приводят в соответствие некоторое количество. Символ является кодом (обозначением) этого количества и имеет соответствующий количественный эквивалент. Например, символ или цифра 7 десятичной системы счисления кодирует известное каждому количество. Алфавит может состоять из положительных и/или отрицательных цифр. Наличие нуля в алфавите необязательно.

Примером позиционной системы счисления является десятичная система счисления,

основание которой P=10 и алфавит A10={0,1,2,3,4,5,6,7,8,9}.

Число в позиционной системе счисления это упорядоченное конечное множество символов:

αnαn-1…αi…α1α0α-1…αm (1)

где αi A - цифра числа, размещенная в позиции i, причем n≥i≥m, n≥0, m≤0.

Позицию цифры в числе называют разрядом числа. Разряд имеет вес. Вес позиции (разряда) i равен Pi. Вес позиции 0 всегда равен единице (P0=1).

Количественный эквивалент цифры в числе зависит от занимаемой ею позиции, и численно равен произведению количественного эквивалента собственно цифры на вес позиции, в которой она размещена. Например, для десятичной системы счисления в числе 137 количественный эквивалент цифры 3 равен 30 (3*101=30).

Число, так же как и цифра, является кодом некоторого количества и, следовательно, имеет количественный эквивалент. Количественный эквивалент числа равен сумме количественных эквивалентов всех его цифр с учетом веса их позиций:

n
N = ∑αi Pi	(2)

m

Максимальное целое число, которое может быть представлено в n разрядах:

Nmax = Pn-1 (3)

Минимальное значащее, не равное 0 число, которое можно записать в m разрядах дробной части:

Nmin = P-m (4)

Позицию с индексом i=0 принято отмечать точкой, а при отсутствии запятой считать, что m=0. Например, запись десятичного числа 137.25 состоит из пяти цифр размещенных в

пяти позициях, три из которых расположены слева от точки, а две других – справа. Количественный эквивалент числа 137,25 определяется следующим образом:

N=1x102 + 3x101 + 7x100 + 2x10-1+6x10-2=137.25

В любой позиционной системе счисления нельзя представить все возможные количества.

Например, в десятичной системе счисления нельзя записать иррациональные, отрицательные и комплексные числа. Чтобы кодировать отрицательные числа введен специальный знак «-» перед записью числа, указывающий на то, что число отрицательно.

Можно построить десятичную систему счисления с основанием P=10 и алфавитом из 10 цифр A={0, 1, 2, 3, 4, 5, 1, 2, 3, 4}, где цифра с черточкой означает, что ее количественный эквивалент отрицателен, например 3= -3. В этой системе счисления можно записывать положительные и отрицательные числа. Например, число 137 имеет количественный эквивалент N = -1x102 + 3x101 + 7x100=-63

2.2. Двоичная система счисления.

Двоичная система счисления имеет основание P=2 и алфавит A2={0,1}. Веса разрядов двоичного числа 2n, 2n-1,… , 21, 20, 2-1, … ,2m-1,2m или 2n, 2n-1, … ,4,2,1,1/2, 1/4,…, 2m-1, 2m.

Например, отрицательное двоичное число -10001001.01 имеет количественный эквивалент:

N=-(1x27+1x23+1x20 + 1x2-2)=-137.25

Чтобы сократить количество используемых символов до двух, знаки числа «+» плюс и «-» минус кодируют соответственно символами 0 и 1. Знак числа приписывают к числу всегда. Поэтому крайний левый разряд в записи числа в ЭВМ является знаковым. Для удобства чтения знаковый разряд числа отделять символом « »

Например, 1 10001001.01 кодирует количество –137.25, 0 10001001.01 кодирует количество +137.25.

Такую запись числа называют прямым кодом.

В ЭВМ количество позиций отводимых для записи числа обычно фиксировано некоторым значением, например 16. Чтобы не указывать в записи каждого числа положение точки, ее фиксируют, например, после 6 разряда справа и в дальнейшем подразумевают. Если количество значащих разрядов в целой или дробной части числа меньше числа позиций отведенных для записи этих частей, то, чтобы заполнить свободные позиции, в них записывают нули. Число, записанное в такой форме, называют числом с фиксированной точкой, представленным в формате фиксированной длины.

Например, запись количественных эквивалентов +137.25 и –137.25 в 16 разрядном формате с точкой фиксированной после 6 разряда справа будет віглядеть следующим образом:

+137.25: 0|010 0010 01.01 0000 -137.25: 1|010 0010 01.01 0000

Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому чаще всего не приемлема при вычислениях. Например, при Р= 2, n = 10 и m = 6 числа изменяются в диапазоне 0,015 < N< 1024.

В форме представления с плавающей запятой каждое число изображается в виде двух групп цифр. Первая группа цифр называется мантиссой, вторая — порядком, причем

абсолютная величина мантиссы должна быть меньше 1, а порядок должен быть целым числом. В общем виде число в форме с плавающей запятой может быть представлено так:

N=±MP±r (3)

где М — мантисса числа (|M|<1); г — порядок числа (целое число); Р — основание системы счисления.

Например, число +137.25 в нормальной форме запишется следующим образом: +0,13725x10-3.

Нормальная форма представления имеет огромный диапазон отображения чисел и является основной в современных компьютерах. Так, диапазон значащих чисел в системе счисления с основанием Р при наличии m разрядов у мантиссы и s разрядов у порядка (без учета знаковых разрядов порядка и мантиссы) будет:

Р-m Р-(Ps-1) < N < (1 - Р-m) Р(Ps-1)

(4)

Например, при P=2 , m=22 и s=10 диапазон чисел простирается примерно от 10-300 до

10300.

В табл.1 приведены диапазоны представления чисел в разных форматах. Таблица 1. диапазоны представления чисел в разных форматах.

			Диапазон представления чисел
Числа
	В формате			При	При
	n	разрядов		n=16	n=32
Целые без знака	0	÷ 2n-1		0 ÷ 65 535	0 ÷ 4 294 967 295
Целые со знаком	± (2n-1-1)			± 32 767	± 2 147 483 647
Правильные дроби	± (1-2-(n-1))			32767	2147483647
со знаком				± 32768	±
						2147483648

Если при вычислении образуется число, целая часть которого имеет количество значащих разрядов, превышающее отведенное для записи целой части в используемом формате, то возникает явление переполнения разрядной сетки. Запись такого числа становится невозможной. Если в дробной части вычисленного числа количество разрядов превышает отведенное в используемом формате для записи дробной части числа, то число округляют до требуемого числа разрядов и переполнения разрядной сетки не возникает. Погрешность представления дробных чисел зависит от способа округления. При округлении методом отбрасывания “лишних” разрядов погрешность не будет превышать веса младшего разряда дробной части результата. Например, при представлении правильной дроби со знаком в формате:

•16 разрядов погрешность не более 1/32 768 ≈ 3.10-5;

•32 разряда погрешность не более 1/2 147 483 648 ≈ 5.10-10.

2.3.Восьмеричная, шестнадцатеричная и двоично-кодированные системы счислениясистема

Запись чисел в двоичной системе счисления содержит длинные цепочки, состоящие из чередующихся 0 и 1, что сильно затрудняет их восприятие и запоминание человеком. Сравните запись десятичного целого +137 с его двоичным эквивалентом 10001001. Для сокращения записи чисел применяют восьмеричную и шестнадцатеричную системы счисления. В тех случаях, когда система счисления не очевидна из контекста, справа к числу принято приписывать индекс, указывающий основание системы счисления, например: 137.2510, 137.258.

В системе с основанием 8 используют алфавит A8={0,1,2,3,4,5,6,7}, а в системе с основанием 16 – A16={0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}. Количественные эквиваленты шестнадцатеричных цифр от A до F приведены в таблице 2.

Веса разрядов числа в восьмеричной системе счисления: 8n,…,512, 64, 8, 1, 1/8, 1/64,

1/512,…, 1/8-m

Веса разрядов числа в шестнадцатеричной системе счисления: 16n,…, 4096, 256, 16, 1,

1/16, 1/256, 1/4096,…, 1/16-m

Например, восьмеричное число 211.28 имеет количественный эквивалент:

N=2x82+1x81+1x80+2x8-1=128+8+1+2/8 = 137.25

Количественный эквивалент шестнадцатеричного целого числа 89.416 равен:

N=8x161+9x160+4x16-1=128+9+4/16 = 137.25

Поскольку основания восьмеричной и шестнадцатеричной систем счисления принадлежат ряду чисел 2n, то преобразования чисел из этих систем счисления в двоичную систему и напротив выполняется весьма просто.

Для преобразования числа из восьмеричной или шестнадцатеричной системы счисления в двоичную достаточно заменить в исходной записи числа каждую цифру ее двоичным эквивалентом. Двоичные эквиваленты цифр этих систем счисления приведены в таблице 2.

Таблица 2. Количественные эквиваленты и двоичные коды цифр от 0 до F.

Цифра	Количественный		Двоичный код цифры
	эквивалент	Восьмеричной	шестнадцатеричной	десятичной
	цифры
0	0	000	0000	0000
1	1	001	0001	0001
2	2	010	0010	0010
3	3	011	0011	0011
4	4	100	0100	0100
5	5	101	0101	0101
6	6	110	0110	0110
7	7	111	0111	0111
8	8		1000	1000
9	9		1001	1001
A	10		1010
B	11		1011
C	12		1100
D	13		1101
E	14		1110
F	15		1111

Например, результат преобразования числа 211.28 в двоичную систему счисления будет 010 001 001.010, а числа 89.4 – 1000 1001.0100.

Нетрудно видеть, что преобразование двоичных чисел в восьмеричные и в шестнадцатеричные сводится к разбиению двоичного числа на группы разрядов по три (на триады) или по четыре (тетрады) разряда в каждой группе в зависимости от того, в восьмеричную или в шестнадцатеричную систему выполняют преобразование. Разбиения выполняют влево и вправо от точки. Затем двоичные коды в каждой группе заменяют цифрой системы счисления, в которую выполняют преобразование.

Системы счисления, цифры которых заменены их двоичными эквивалентами,

называют двоично-кодированными системами счисления.

Примером двоично-кодированной системы счисления является широко используемая десятичная двоично-кодированная система счисления. В этой системе десятичные цифры от 0 до 9 заменены их четырехразрядными двоичными эквивалентами. Например, десятичное число 137.25 будет записано как 0001 0011 0111. 0010 0101. Однако, если рассматривать эту двоичную последовательность как двоичное число, то окажется, что его количественный эквивалент не совпадает с количественным эквивалентом исходного десятичного числа:

N=1x28+1x25+1x24+1x22+1x21+1x20+1x2-3+1x2-6+1x2-8=311 37/256 ≠137.25.

2.4. Преобразование чисел из десятичной в двоичную, восьмеричную, шестнадцатеричную системы счисления и наоборот

Перевод чисел в десятичную систему осуществляется путем составления степенного ряда (2) с основанием той системы, из которой число переводится. Затем подсчитывается значение суммы.

Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.

Пример: преобразуем десятичное целое 137 в системы счисления с основаниями 16, 8 и 2.

137		16
128		8
9
Результат: 137 = 8916
137		8
136		17			8
1		16			2
		1
Результат: 137 = 2118
137		2
136		68			2
1		68			34		2
		0		34			17		2
					0		16		8			2
							1		8			4		2
									0		4			2		2
												0	2			1
														0
Результат: 137 = 100010012

На практике при преобразовании десятичного числа в двоичное удобнее выполнить вначале его преобразование в шестнадцатеричное или в восьмеричное число, а затем заменить двоичным эквивалентом.

Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого. В общем случае результат может содержать бесконечное количество разрядов. Поэтому вычисления выполняют до получения требуемого числа разрядов с учетом последующего округления.

Пример: преобразуем десятичную дробь 0,25 в системы с основаниями 2, 8 и 16.

0,25 × 2=0,5	0,25 × 8=2	0,25 × 16=4
0,5 × 2=1,0
Результат: 02510 = 0.012	Результат: 02510 = 0.28	Результат: 02510 = 0.416

Преобразование смешанного десятичного числа в смешанное число в системе с основанием 2n выполняют в два приема. Раздельно преобразовывают целые и дробные части числа. Полученные результаты приписывают один к другому.

Так, например, результат преобразования десятичного числа 137.2510 в шестнадцатеричную систему счисления будет 89.416.

Лекция 3

Алгебраическое представление чисел

3.1. Прямой, обратный, дополнительный код.

Для алгебраического представления чисел, то есть для представления чисел с учетом их знака, в вычислительных машинах используются специальные коды:

•прямой код числа;

•обратный код числа;

•дополнительный код числа.

Выполнение арифметических операций алгебраического сложения и вычитания чисел в прямых кодах в системах счисления с положительным основанием и положительными цифрами алфавита требует предварительного анализа знаков операндов, сравнения их модулей и последующего принятия решения о том, что необходимо выполнять фактически – сложение или вычитание.

Для упрощения алгоритмов выполнения операций в подобных системах счисления используют представление числа в обратном или дополнительном кодах и выполняют операции над числами, представленными в этих кодах.

Запись числа αnαn-1…αi…α1α0α-1…αm , где αn {0,1} – знак числа, при всех прочих равных условиях имеет разные количественные эквиваленты в зависимости от того в каком

коде, прямом, обратном или дополнительном, оно записано.

Положительные числа (αn=0) в прямом, обратном и дополнительном кодах записываются одинаково и их значащие разряды αn-1÷αm кодируют количественный эквивалент числа. Различие состоит в способе записи отрицательных чисел (αn=1).

Значащие разряды αn-1÷αm отрицательного числа N кодируют:

•в прямом коде – модуль количественного эквивалента |N|;

•в обратном коде - дополнение модуля количественного эквивалента до веса знакового разряда, уменьшенного на вес младшего разряда, т.е. величину (Pn-Pm)-

|N|.

•в дополнительном коде – дополнение модуля количественного эквивалента до веса знакового разряда Pn, т.е. величину Pn-|N|;

Например, число –137,25 в десятичной P=10 и в двоичной P=2 системах счислениях в разных кодах записывают так:

1|137.25пр		1|862.74обр	1|862.75доп
1 10001001.01пр		1 01110110.10обр	1 01110110.11доп
Формулы для вычисления количественного эквивалента кода
		n−1
•	прямого	Nпр = (−1)an ∑αi Pi	(5)
		m
		n−1
•	дополнительного	Nдоп = −an Pn +∑ai Pi ,	(6)
		m
		n−1
•	обратного	Nобр = −an (Pn − Pm ) +∑ai Pi .	(7)

m

Прямой, обратный и дополнительный коды обладают следующими свойствами.

Впрямом и обратном кодах количество ноль можно записать двумя способами. В

прямом коде: +010 или –010; 0|00...02 или 1|00...02.

Вобратном коде +9 или-9; 0|11...12 или 1|11...12.

Впрямом и обратном кодах диапазоны представления положительных и отрицательных чисел одинаковы и симметричны относительно нуля. Модуль минимального числа равен максимальному числу.

Вдополнительном коде количество ноль можно записать только одним способом как +0. Отрицательный ноль в дополнительном коде не существует.

Вдополнительном коде диапазоны представления положительных и отрицательных

чисел не симметричны относительно нуля. Модуль минимального числа превышает максимальное число на величину равную весу младшего разряда Pm. Код минимального числа

вдополнительном коде 1|00...0 при любом натуральном P, а его количественный эквивалент - Pn.

Минимальное число представимое в дополнительном коде (-Pn) нельзя записать в прямом или в обратном коде, сохранив разрядность кодов.

3.2. Преобразование кодов.

При преобразовании кодов необходимо учитывать следующие особенности, вытекающие из свойств кодов.

1. При преобразовании дополнительного кода в прямой или обратный коды необходимо увеличить формат числа на один старший значащий разряд. При всех других преобразованиях формат числа сохраняется.

Необходимость увеличения формата при преобразовании дополнительного кода вызвана тем, что минимальное число представимое в дополнительном коде (-Pn) нельзя записать в прямом или в обратном коде, сохранив разрядность кодов. Например, при P=10 код 1|000доп имеет количественный эквивалент –103. Это значение в прямом и в обратном кодах 1|1000пр и 1|8999обр содержит дополнительный старший значащий разряд. Аналогично, при P=2 код 1|000доп имеет количественный эквивалент –23, что соответствует кодам 1|1000пр

(-8) и 1|0111обр.

2. При преобразовании прямого или обратного кода в дополнительный код знак числа может измениться. Изменение знака может произойти в единственном случае, когда в прямом или обратном коде записано число (-0), которое в дополнительном коде придется записать как (+0). При всех других преобразованиях знак числа сохраняется.

Например, при P=10 коды 1|000пр (-0) и 1|999обр (-0) соответствуют коду 0|000доп (+0). Аналогично, при P=2 коды 1|000пр(-0) и 1|111обр (-0) соответствуют коду 0|000доп (+0).

Преобразование положительных чисел из одного кода в другой.

При преобразовании положительных чисел из одного кода в другой код числа не изменяются за исключением случаев преобразования дополнительного кода в прямой или в обратный код.

Пример. В примерах A,C и E показаны преобразования из прямого кода в обратный и дополнительный код и из обратного кода в прямой и в дополнительный код. В примерах B,D и F показаны преобразования из дополнительного кода в прямой и обратный код.

	A	B		C	D		E	F
	P=10	P=10					P=2	P=2
Xпр: 0|137		Xдоп: 0|137	Xпр: 0|000		Xдоп: 0|000	Xпр: 0|101		Xдоп: 0|101
Xобр:	0|137	Xпр: 0|0137	Xобр:	0|000	Xпр: 0|0000	Xобр:	0|101	Xпр: 0|0101
Xдоп:	0|137	Xобр: 0|0137	Xдоп:	0|000	Xобр: 0|0000	Xдоп:	0|101	Xобр: 0|0101

Преобразование прямого кода отрицательного числа в обратный код и обратного кода отрицательного числа в прямой код.

Для преобразования прямого кода отрицательного числа в обратный код или обратного кода в прямой достаточно заменить цифры значащих разрядов обратными им. Содержимое знакового разряда остается без изменения.

Преобразование обратного кода отрицательного числа в дополнительный код.

Для преобразования обратного кода отрицательного числа в дополнительный код достаточно прибавить 1 к младшему разряду обратного кода. Знаковый разряд должен участвовать в операции сложения наравне со значащими. Сложение в знаковом разряде должно выполняться в двоичном коде, и перенос из знакового разряда в следующий должен быть отброшен.

Преобразование прямого кода отрицательного числа в дополнительный код можно выполнить разными способами:

•преобразовать прямой код в обратный, и затем обратный код в дополнительный по изложенным выше правилам;

•вычесть из прямого кода, включая его знаковый разряд, константу Pm, и затем заменить цифры в значащих разрядах полученного кода на обратные им;

•вычесть прямой код числа, включая его знаковый разряд, из константы Pn.

Рассмотрим первый способ преобразования на примере:

	A			B		C	D	E	F	G
	P=10			P=10		P=2	P=2	P=2	P=8	P=16
Xпр: 1|600 (-600)			1|000 (-0)			1|0101 (-5)	1|0100 (-4)	1|0000 (-0)	1|450	1|A70
Xобр: 1|399 (-600)			1|999		(-0)	1|1010 (-5)	1|1011 (-4)	1|1111	1|327	1|58F
+ 1			+ 1			+ 1	+ 1	+ 1	+ 1	+ 1
Xдоп:	1|400	(-600)		0|000	(+0)	1|1011 (-5)	1|1100 (-4)	0|0000 (+0)	1|330	1|590

В следующем примере выполняется вычитание 1 из прямого кода числа, и затем значащие цифры полученного кода заменяются на обратные. При вычитании заем из знакового разряда отбрасывается.

A

B

C

D

E

F

G

P=10

P=10

P=2

P=2

P=2

P=8

P=16

Xпр: 1|600 (-600)

1|000 (-0)

1|0101 (-5)

1|0100 (-4)

1|0000 (-0)

1|450

1|A70

-

1

- 1

-

1

(-4)

-

1

-

1

-

1

-

1

1|599

0|999

1|0100

1|0011 (-3)

0|1111 (-0)

1|447

1|A6F

Xдоп: 1|400 (-600)

0|000 (+0)

1|1011 (-5)

1|1100 (-4)

0|0000 (+0)

1|330

1|590

В следующем примере выполняется вычитание прямого кода числа из константы Pn. Заем из знакового разряда отбрасывается.

Сопоставляя примеры, можно убедиться в том, что при одинаковом значении исходного данного и разных способах вычисления, результаты совпадают.

A

B

C

D

E

F

G

Pn:

P=10

P=10

P=2

P=2

P=2

P=8

P=16

1 000

1 000

1 0000

1 0000

1 0000

1 000

1 000

Xпр:

1|600 (-600)

1|000

(-0)

1|0000 (-0)

1|450

1|A70

1|0101 (-5)

1|0100 (-4)

Xдоп:

(-600)

0|000

(+0)

1|1011 (-5)

1|1100

(-4)

0|0000 (+0)

1|330

1|590

1|400

Преобразование дополнительного кода отрицательного числа в обратный и прямой

коды.

Так как в дополнительном коде значащие разряды отрицательного числа имеют количественный эквивалент Pn-|N|, то для определения значащих разрядов

• прямого кода достаточно вычислить
Pn-(Pn-|N|)=|N| или	(6)
((Pn-Pm)-(Pn-|N|))+Pm=|N| или	(7)
(Pn-Pm)-((Pn-|N|)-Pm)=|N|;	(8)
• обратного кода достаточно вычислить
(Pn-|N|)-Pm=(Pn-Pm)-|N| или	(9)
(Pn-Pm)-(((Pn-Pm)-(Pn-|N|))+Pm)= (Pn-Pm)-|N|.	(10)

Рассмотрим преобразования на примерах. Вычисляется прямой код в соответствии с

(6). Из константы Pn вычитаются значащие разряды дополнительного кода числа. Заем из старшего значащего разряда отбрасывается. Знаковый разряд копируется. Формат значащих разрядов результата расширяется до формата константы.

A

B

C

D

E

F

G

Pn:

P=10

P=10

P=2

P=2

P=2

P=8

P=16

1000

1000

10000

10000

10000

1000

1 000

Xдоп:

1| 400 (-600)

1| 000 (-103)

1| 1011 (-5)

1| 1100 (-4)

1| 0000 (-16)

1| 330

1| 590

Xпр:

1|

(-600)

1

(-103)

1

(-5)

1|

(-4)

0600

|1000

|00101

00100

1|10000

(-16)

1|0450

1|0A70

В следующем примере в вариантах A,B,C и D вычисляется прямой код в соответствии с

(7). Для получения значения выражения (Pn-Pm)-(Pn-|N|) цифры значащих разрядов дополнительного кода числа заменяются на обратные им. К полученному коду значащих разрядов прибавляется Pm, причем перенос из старшего значащего разряда фиксируется в дополнительном старшем значащем разряде результата. Знаковый разряд исходного кода копируется в знаковый разряд результата.

A

B

C

D

E

F

G

H

P=10

P=10

P=2

P=2

P=10

P=10

P=2

P=2

Xдоп: 1|400 (-600)

1|000 (-103) 1|1011 (-5)

1|0000 (-16)

1|400 (-600) 1|000 (-103)

1|011

(-5) 1|000 (-8)

599

999

0100

1111

- 1

- 1

- 1

- 1

+ 1

+ 1

+ 1

+ 1

399

999

010

111

Xпр: 1|

(-600)

1|

0600

1000

(-103) 1|00101

(-5)

1|10000 (-16)

1|0600 (-600) 1|1000 (-103) 1|0101

1|1000

Ввариантах E,F,G и H вычисляется прямой код в соответствии с (8). Выполняется вычитание из значащих разрядов дополнительного кода значения Pm, причем заем из старшего значащего разряда фиксируется в дополнительном старшем значащем разряде результата. Цифры значащих разрядов промежуточной разности заменяются на обратные им. Знаковый разряд исходного кода копируется в знаковый разряд результата.

Вследующем примере вычисляется обратный код в соответствии с (9). С целью расширения разрядной сетки результата к значащим разрядам дополнительного кода приписывается слева цифра с количественным эквивалентом P–1, что не изменяет

количественный эквивалент дополнительного кода. Из расширенного дополнительного кода вычитается Pm. Знаковый разряд исходного кода можно копировать в знаковый разряд результата.

	A				B			C					D
P=10				P=10				P=2					P=2
Xдоп: 1|400 (-600)				1|000 (-103)			1|1011					1|0000 (-16)
Xдоп: 1|9400 (-600)				1|9000 (-103)			1|11011				(-5)	1|10000 (-16)
- 1				-	1	(-103)	-		1			-	1
Xобр: 1|	9399		(-600)	1|	8999		1|	11010			(-5)	1|	01111		(-16)

Некоторые возможности упрощения преобразований двоичного прямого или обратного кода в дополнительный и наоборот.

В двоичной системе счисления цифры в младшем разряде прямого и дополнительного кода совпадают всегда. Цифры младшего разряда обратного и дополнительного кода инверсные. Эти свойства двоичной системы счисления позволяют упростить любые из рассмотренных выше вариантов взаимных преобразований кодов: прямой - дополнительный и обратный – дополнительный.

Если копировать младший разряд Xпр в Xдоп, то нет необходимости вычислять инверсию этого разряда и прибавлять к нему 1. Перенос в разряд x1 из разряда x0 всегда равен инверсии младшего разряда Xпр.

Таким образом, для преобразования прямого кода отрицательного двоичного числа в дополнительный код достаточно инвертировать цифры значащих разрядов прямого кода, кроме цифры младшего разряда, и, если младший разряд равен 0, прибавить 1 ко второму разряду полученного кода.

Следовательно, для преобразования прямого кода отрицательного двоичного числа в дополнительный код достаточно инвертировать все цифры старших значащих разрядов исходного кода размещенные слева от первой 1 обнаруженной при просмотре разрядов справа налево. Исключение из правила: код 1|00…0 (-0) следует замещать кодом

0|00…0 (+0). Например:

Xпр:	1|0010000	1|1011100	1|1011001	1|1000000	1|0000000
Xдоп:	1|1110000	1| 0100100	1|0100111	1|1000000	0|0000000

Для преобразования дополнительного кода отрицательного двоичного числа в прямой код достаточно инвертировать цифры значащих разрядов дополнительного кода, кроме цифры младшего разряда, и, если младший разряд равен 0, прибавить 1 ко второму разряду полученного кода. Дополнительный старший значащий разряд результата принять равным 0 или значению переноса из старшего значащего разряда, если выполнялось сложение.

Лекция 4

Арифметические операции с двоичными числами

В настоящем разделе рассмотрим некоторые правила выполнения основных арифметических операций над числами в системах счисления с основанием 2, 8, 10 и 16 представленных в прямом, обратном или дополнительном коде.

4.1. Операция изменения знака

Выполнение операции изменения знака числа сводится

•в прямом коде - к инвертированию знакового разряда кода;

•в обратном коде – к инвертированию знакового разряда и замене цифр всех значащих разрядов кода обратными;

•в дополнительном коде – к инвертированию знакового разряда и к вычислению

дополнения значащих разрядов кода до веса знакового разряда.

Правило изменения знака в прямом коде очевидно. Правила изменения знака в обратном и дополнительном кодах следуют из правил преобразования прямого кода в обратный или в дополнительный код и наоборот, но не совпадают с последними. При преобразовании кодов знак сохраняется, а при изменении знака он инвертируется. В остальном правила аналогичны.

Внимание. В дополнительном коде нельзя изменить знак минимального числа (отрицательного максимального по модулю) при сохранении формата. Это следует из асимметрии представления чисел в дополнительных кодах. Если формат расширять нельзя, то изменению знака должна предшествовать проверка кода операнда на значение 1 00…0доп с последующим блокированием выполнения операции либо приняты меры для исключения образования этого значения на предшествующих этапах вычислений.

Следующие примеры пар кодов иллюстрируют результаты изменения знака операнда в различных кодах и системах счисления:

0 1011 1002п	0 1011 1002о	0 3764 4308о		0 1011 1002д	0 7345 4268п
1 1011 1002п	1 0100 0112о	1 4013 3478о		1 0100 1002д	1 7345 4268п
0 7657 1008д	0 9AF0 3616о	1 F876 AB016д		1 4019 34710о	1 9876 20010д
1 0120 7008д	1 650F C916о	0 0789	550	0 5980 65210о	0 0123 80010д
		16д

4.2. Сложение

Операция алгебраического сложения в дополнительном коде

Как было отмечено ранее, алгоритмы выполнения операции алгебраического сложения в прямых кодах относительно сложны. В обратном и дополнительном кодах сложение выполняется проще, поскольку не возникает необходимость в анализе знаков операндов, в сравнении их модулей и т.п.

Сложение в дополнительном коде сводится к сложению одноименных разрядов чисел, начиная с младшего разряда включая знаковый разряд, с учетом переноса из предыдущего разряда. Знаковые разряды складываются по правилам сложения двоичных цифр с учетом переноса из предшествующего разряда. Перенос из знакового разряда отбрасывается. Полученный результат представлен в дополнительном коде.

Рассмотрим примеры сложения чисел в дополнительном коде. При их анализе обратите внимание на то, как складываются знаковые разряды.

Пусть операнды - десятичные числа –231,15 и +215,04. Их сумма равна –016,11. Дополнительные коды операндов и суммы соответственно равны 1 768.85 0 215.04 и 1 983.89. Выполним сложение операндов в дополнительном коде:

1 768.85

0 215.04

Дополнительный код суммы: 1 983.89

Пусть десятичные операнды равны –231,15 и –215,04. Их сумма равна -446,19. Дополнительные коды операндов и суммы: 1 768.85, 1 784.96 и 1 553.81. Выполним сложение дополнительных кодов слагаемых:

	1 768.85
	1 784.96
Дополнительный код суммы:	1 553.81

Примеры сложения двоичных чисел в дополнительном коде:

0 10100111.011		(+1673/8)				1 01111001.101	(-1343/8)			1 01111001.101(-1343/8)
0 01010011.101		(+835/8)				0 01110001.011	(+1133/8)			1 10001110.101		(-1133/8)
												(-2476/8)
0 11111011.000		(+251)				1 11101011.000	(-21)			1 00001000.010

При сложении одноразрядных двоичных, восьмеричных или шестнадцатеричных чисел следует пользоваться таблицами сложения цифр в этих системах счисления или следующим правилом. Если количественному эквиваленту суммы цифр соответствует цифра из алфавита системы счисления, то перенос в следующий разряд равен нулю, а сумма равна цифре соответствующей количественному эквиваленту суммы. Если количественный эквивалент суммы цифр больше количественного эквивалента максимальной цифры алфавита, то перенос в следующий разряд равен единице, а цифра суммы имеет количественный эквивалент суммы уменьшенный на основание системы счисления.

Например, в восьмеричной системе счисления 3+2=5 и перенос равен 0. Сумма 4+6=2 и перенос равен 1, так как количественный эквивалент суммы 4+6>7 (4+6=1010), а количественный эквивалент единицы переноса в восьмеричной системе счисления равен 8.

В шестнадцатеричной системе счисления 4+6=А (А имеет количественный эквивалент 1010) и перенос равен 0. Сумма 4+А=Е (Е=1410) и перенос равен 0. Сумма А+А=4 и перенос равен 1 так как вес переноса равен 1610, а А+А=2010.

Примеры сложения шестнадцатеричных чисел в дополнительных кодах.

0 A7.6	(+1673/8)	1 79.A	(-1343/8)	1 79.A	(-1343/8)	1 08.4	(-2476/8)
0 53.A	(+835/8)	0 71.6	(+1133/8)	1 8E.A	(-1133/8)	1 F7.C	(-82/8)
0 FB.0	(+251)	1 EB.0	(-21)	1 08.4(-2476/8)		1 00.0	(-256)

Минимальное число представимое в выбранной разрядной сетке в дополнительном коде. Нельзя изменять знак этого числа из-за асимметрии представления чисел в дополнительном коде

Операция алгебраического сложения в обратном коде

Сложение в обратном коде выполняется также как и в дополнительном коде, но с той разницей, что перенос из знакового разряда не отбрасывается, а прибавляется к младшему разряду промежуточной суммы. Этот перенос называют циклическим. Результат сложения будет получен в обратном коде.

Примеры сложения двоичных чисел в обратном коде:

		0 0 00001111 11									0 0 11100010 00													11 11111111 00
						0 10100111.011		(+1673/8)								1 01111001.100 (-1343/8)												1 01111001.100				(-1343/8)
						0 01010011.101		(+835/8)								0 01110001.011			(+1133/8)									1 10001110.100				(-1133/8)
						0 11111011.000										1 11101010.111												1 00001000.000
							0	(+251)									0													1		(-2476/8)
																			(-21)
						0 11111011.000										1 11101010.111													1 00001000.001

Примеры сложения восьмеричных чисел в обратном коде:

		00 011									00 100											11 111										00 000
					0 247.3 (+1673/8)										1 571.4				(-1343/8)				1 571.4 (-1343/8)														1 410.1			(-2476/8)
					0 123.5			(+835/8)							0 161.3 (+1133/8)										1 616.4			(-1133/8)									0 367.6 (+2476/8)
					0 373.0
															1 752.7								1 410.0														1 777.7
						0											0										1											0
								(+251)										(-21)										(-2476/8)												(-0)
					0 373.0										1 752.7								1 410.1														1 777.7
		Попробуйте выбрать операнды так, чтобы сумма их была равна 0 000.0																											(+0). Решение существует.

Сложение в обратном коде можно начинать с любого, необязательно с младшего разряда, что в некоторых случаях может быть полезно при реализации устройств.

Циклическое распространение переноса при сложении является серьезным недостатком обратного кода по сравнению с дополнительным кодом. Поэтому, несмотря на простоту преобразования прямого кода в обратный код и наоборот, и на простоту изменения знака числа в обратном коде, обратный код сравнительно редко применяют в устройствах вычислительной техники и автоматики.

Переполнение разрядной сетки при сложении

При ограниченной разрядной сетке диапазон представления чисел ограничен. Поэтому сумма двух операндов принадлежащих диапазону может оказаться за его пределами, что приведет к существенной ошибке в вычисленной сумме. Например, пусть в двоичном дополнительном пятиразрядном коде представлены целые положительные операнды со знаком 0 0111 (+7) и 0 1100 (+12). Сложим их по правилу сложения в дополнительном коде.

0 0111 (+7)

Величина ошибки недопустимо велика и вызвана выходом правильного

значения

суммы 0 10011

(+19)

за

пределы

диапазона

(+15; -16)

0 1100 (+12)

представления целых со

знаком

в двоичном

дополнительном коде в

1 0011

(-13)

выбранной

пятиразрядной

сетке.

Такое

явление

называют

переполнением разрядной сетки.

В ЭВМ применяют аппаратуру контроля переполнения разрядной сетки, назначение которой состоит в формировании сигнала R=1 при переполнении. В основу функционирования аппаратуры контроля могут быть положены различные алгоритмы.

Очевидно, что при сложении операндов с разными знаками модуль суммы меньше модуля любого из операндов. Поэтому при разных знаках операндов результат не может выйти за пределы диапазона представления чисел и, следовательно, R=0.

Переполнение разрядной сетки суммы может возникнуть только при одинаковых знаках операндов.

Если операнды положительны и их сумма не укладывается в диапазон представимых чисел, то при их сложении в дополнительном коде образуется перенос из старшего значащего разряда в разряд знака, который приводит к формированию ошибочного отрицательного результата. Поэтому признак переполнения при положительных операндах

an an-1…a1a0a-1a-2…am и bn bn-1…b1b0b-1b-2…bm можно описать двумя вариантами булевого выражения: an bn Sn или an bn pn, где Sn – знаковый разряд суммы; pn – перенос в знаковый

разряд.

Если оба операнда отрицательны и сумма выходит за пределы диапазона представляемых чисел, то отсутствие переноса в знаковый разряд приводит к ошибочному положительному результату. Поэтому признаки переполнения при отрицательных операндах - положительный знак результата или отсутствие переноса в знаковый разряд: an bn Sn или

an bn pn.

Сказанное позволяет определить булевы уравнения, описывающие варианты комбинационных схем вычисляющих признак переполнения разрядной сетки суммы:

R= an bn	Sn+ an bn Sn, (5)
R= an bn	pn+ an bn pn. (6)

Если R=1, то код суммы содержит ошибку.

Существует простой способ ее устранить. Для этого достаточно

-в двоичной системе счисления приписать к ошибочному результату слева знаковый разряд любого из операндов;

-в восьмеричной, десятичной и шестнадцатеричной системах счисления приписать к

ошибочному результату слева знаковый разряд любого из операндов и, если знаковый разряд ошибочного результата равен нулю, заменить его на 6, 8 или E соответственно.

Например,

					При P=2														При P=16													При P=10
				0 0111	(+7)					1 1001		(-7)					0 B9		(+185)					1 47		(-185)					0 87	(+87)				1 13		(-87)
				0 1100	(+12)					1 0100		(-12)					0 72		(+114)					1 8E		(-114)					0 25	(+25)				1 75		(-25)
				1 0011	(-13)							(+13)							(-213)							(+213)						(-88)
										0 1101							1 2B							0 D5							1 12					0 88		(+88)
0 1 0011					(+19)				1 0 1101			(-19)			0 1 2B				(+299)				1 E D5			(-299)			0 1 12			(+112)		1 8 88 (-112)

4.3. Вычитание

Вычитание в дополнительном коде сводится к вычитанию одноименных разрядов чисел, начиная с младшего разряда и включая знаковый разряд, с учетом заёма из предыдущего разряда. Знаковые разряды вычитаются по правилам вычитания двоичных цифр с учетом заёма из предшествующего разряда. Заём из знакового разряда отбрасывается. Полученный результат представлен в дополнительном коде.

Примеры вычитания двоичных чисел в дополнительном коде:

		0 101 00111.011	(+1673/8)		1 01111001.101	(-1343/8)		1 01111001.101	(-1343/8)
		0 010 10011.101	(+835/8)		0 01110001.011	(+1133/8)		1 10001110.101	(-1133/8)
		0 010 10011.110	(+836/8)		1 00001000.010	(-2476/8)		1 11101011.000	(-21)

Примеры вычитания шестнадцатеричных чисел в дополнительном коде:

0 A7.6

(+1676/16)

1 79.A

(-1346/16)

1 79.A

(-1346/16)

1 08.4

(-24712/16)

0 5

3.A

(+8310/16)

0 71.6

(+1136/16)

1 8E.A

(-1136/16)

1 F7.C

(-8 4/16)

0 5

3.С

(+8312/16)

1 08.4

(-24712/16)

1 EB.0

(-21)

(-239 8/16)

1 10.8

Знаковые разряды вычитаются по правилам вычитания в двоичной системе счисления. Разность в дополнительном коде

Вычитание в обратном коде отличается от вычитания в дополнительном коде тем, что заём из знакового разряда не отбрасывается, а вычитается из младшего разряда промежуточной разности. Этот заём называют циклическим. Результат вычитания будет получен в обратном коде. Вычитание можно выполнять, начиная с любого разряда.

Примеры вычитания двоичных чисел в обратном коде:

			0 0 10 10 011 1 00						0 0 000 00 000 11								1 1 000 11 100 00
				0 10100111.011 (+1673/8)							1 01111001.100			(-1343/8)					1 01111001.100			(-1343/8)
				0 01010011.101 (+835/8)							0 01110001.011			(+1133/8)					1 10001110.100			(-1133/8)
				0 01010011.110							1 00001000.001								1 11101011.000
	-
						0	(+836/8)		-			1		(-2476/8)		-					1
				0 01010011.110							1 00001000.001								1 11101010.111			(-21)
												Разность в обратном коде

Переполнение разрядной сетки при вычитании

Переполнение разрядной сетки при вычитании может произойти только при разных знаках операндов. Если знак уменьшаемого 0, а вычитаемого 1, то знак разности должен быть 0. При переполнении разрядной сетки знак разности будет 1 из-за отсутствия заёма. Поэтому признак переполнения можно описать выражениями: an bn dn или an bn un, где dn – знаковый разряд разности; un – заём из знакового разряда.

Если знак уменьшаемого 1, а вычитаемого 0, то знак разности должен быть 1. В этом случае признак переполнения описывается выражениями: an bn dn или an bn un.

Признак переполнения при вычитании описывается уравнениями:

R= an bn dn + an bn dn, (1-6) R= an bn un + an bn un. (1-7)

При R=1 дополнительный код правильного значения разности можно получить, приписав к результату слева знак уменьшаемого и считать, что все остальные разряды являются значащими. Например:

Заёмы: 1 0 001 100 0 1 00							0 1 000 01 100 10
				0 10100111.011 (+1673/8)						1 01111001.101 (-1343/8)
				1 10001110.101		(-1133/8)				0 10100111.011 (+1673/8)
						(-2316/8)					(+1622/8)
				1 00011000.110			011010010.010
		0 1 00011000.110				(+2806/8)	1 011010010.010				(-3016/8)

Замена операции вычитания сложением и наоборот

Можно вычислить разность Z=X-Y не путем вычитания Y из значения X, а посредством сложения X с (-Y). Действительно:

Z=X-Y= X+(-Y).

Это позволяет не строить устройство для вычитания (вычитатель), из устройства изменения знака и сумматора.

Напротив, можно исключить выполнение операции сложения, заменив ее операциями изменения знака второго операнда с последующим вычитанием его из первого операнда. Действительно:

Z=X+Y= X- (-Y).

Эта возможность никак не зависит от системы счисления и от того, в каких кодах выполняется сложение или вычитание.

4.4. Операция алгебраического умножения

Умножение в прямом коде.

Результат умножения в прямом коде двух операндов без знака содержащих n и m значащих разрядов имеет n+m значащих разрядов. В частном случае, если n=m разрядность результата вдвое превышает разрядность операндов.

При умножении операндов со знаком и n значащими разрядами образуется произведение, содержащее 2n+1 разряд. Поэтому при записи произведения в формате, вдвое превышающем формат операндов, существует слева один избыточный значащий разряд, в который следует записывать 0. Например, если операнды со знаком представлены в прямом коде в шестнадцатиразрядном формате, то значащих разрядов 15, а разрядность произведения, включая его знак, 2×15+1=31. Поэтому в 32 разрядный формат придется записывать 0 в разряд, следующий за разрядом знака.

Знак произведения вычисляют путем сложения по модулю 2 знаковых разрядов операндов. Значащие разряды произведения вычисляют, перемножая операнды как числа без знака. Результат умножения XY целых без знака должен быть равен результату Y- кратного сложения X с самим собой. Дробные числа перемножают как целые, а положение запятой в произведении определяют, отсчитывая, справа налево столько разрядов, сколько дробных разрядов в операндах вместе.

При умножении вычисляют частные произведения множимого X на каждый разряд множителя Y. Суммируют частные произведения с учетом веса каждого из них равного весу разряда множителя. Вес частного произведения учитывают сдвигом его влево на необходимое число разрядов относительно частного произведения X на младший разряд Y.

При вычислении частных произведений в системе счисления с основанием P>2 необходимо учитывать переносы в старшие разряды, возникающие при умножении цифры X на цифру Y. В двоичной системе такие переносы отсутствуют, что существенно упрощает процесс умножения в двоичной системе счисления.

Таблицы умножения цифр системы счисления можно получить, перемножив количественные эквиваленты ее цифр и представив результаты в этой системе счисления. Например, произведение цифр 9×F шестнадцатеричной системы счисления имеет количественный эквивалент 910×1510=13510, или 8716. Следовательно, результат в данном разряде равен 716, и перенос в следующий разряд равен 816.

В двоичной системе счисления частное произведение X на цифру Y равно 0, если цифра Y равна 0, или оно равно X, если цифра Y равна 1. Это существенно упрощает вычисление частных произведений в двоичной системе.

Например, пусть необходимо перемножить прямые двоичные коды чисел 0 1101.01 и 1 1011.10. Определим знак результата: 0 1=1 – знак произведения минус. Найдем матрицу

частных произведений значащих разрядов:

0|

1101.01

Первая и предпоследняя строки

матрицы

нулевые,

так

как они

содержат частные произведения X на младший и предпоследний разряды Y

1|

1011.10

000000

равные нулю. Остальные строки содержат X, так как соответствующие им

разряды Y содержат

1. Каждое последующее

частное

произведение

110101

сдвинуто на разряд влево относительно предыдущего, чтобы учесть его

110101

вес.

110101

Произведение

можно вычислять

путем

суммирования

частных

000000

	110101	произведений так, как это обычно делают в десятичной системе счисления.
		Причем порядок суммирования цифр столбца и переносов в столбец не
	1|10011000.0110
		играет роли.

Умножение в дополнительном коде.

Если операнды представлены в дополнительном коде и содержат по n значащих разрядов, то количество значащих разрядов в их произведении равно 2n+1 независимо от того, в каком коде (прямом, обратном или дополнительном) будет получен результат. Это на один разряд больше, чем при умножении в прямом коде Поэтому, например, при умножении

двоичных дополнительных кодов операндов представленных в 16 разрядном формате необходимо для хранения произведения использовать все разряды 32 разрядного формата.

Старший дополнительный значащий 2n+1 разряд дополнительного кода положительного произведения принимает значение 1 только в том случае, когда оба операнда отрицательны и все их значащие разряды равны 0. Это вызвано асимметрией представления чисел в дополнительном коде. Дополнительный значащий 2n+1 разряд отрицательного произведения всегда содержит цифру обратную нулю: 1 в двоичной, 9 в десятичной, F в шестнадцатеричной системах счисления.

Например. Пусть в десятичной системе счисления X=Y=1|00доп (-10010). Тогда произведение XY=0|10000 (+1000010) и содержит 5, а не 4, как можно было бы ожидать, значащих разрядов.

Знак произведения равен сумме по модулю 2 знаковых разрядов операндов.

Таким образом, по крайней мере, два разряда произведения – знаковый и дополнительный - можно вычислять, не выполняя собственно умножения.

Остальные разряды дополнительного кода произведения можно вычислять разными способами. Рассмотрим некоторые из них.

Умножение в дополнительном коде выполняется с промежуточным преобразованием операндов в прямой код и результата – в дополнительный. Очевидно, что изложенный способ умножения дополнительных кодов операндов значительно сложнее способа умножения в прямом коде, что усложняет аппаратуру и замедляет процесс вычислений.

Умножение без преобразования в прямой код с введением корректирующих поправок в результат.

Если перемножать значащие разряды дополнительных кодов операндов так, как это делали в прямом коде, то результат получится верным, если знаки операндов положительные. Это следует из того, что дополнительные коды положительных операндов и положительного результата совпадают с их прямыми кодами. При отрицательных знаках операндов результат умножения ошибочен.

Выполним анализ ошибки. Найдем значение результата умножения отрицательных чисел и сравним его с правильным значением.

Пусть операнды X<0, а Y≥0. Так как операнды представлены в дополнительном коде,

то количественные эквиваленты значащих разрядов их					кодов будут равны Pn − X	и |Y|.
Здесь Pn – вес знакового разряда (n≥0), а Pn −		X		-	дополнение значения |X|	до Pn.

Количественный эквивалент кода значащих разрядов произведения, полученного по правилу умножения в прямом коде, будет равен

(Pn − X )Y = Pn Y − XY . (1-8)

Так как правильное значение результата должно быть представлено в дополнительном коде, то его значащие разряды должны содержать код дополнения XY до

веса знакового разряда произведения. Знаковый разряд произведения должен иметь вес P2n+1, так как количество разрядов в целой части произведения при умножении удваивается и образуется один дополнительный значащий разряд. Следовательно, количественный эквивалент значащих разрядов дополнительного кода произведения должен быть равен

P2n+1 − XY . (1-9)

Очевидно, что код результата содержит ошибку, и ее количественный эквивалент

(P2n+1 − XY )- (Pn Y − XY ) =Pn(Pn+1-|Y|). (1-10)

Аналогично, при X≥0 и Y<0 код результата содержит ошибку Pn(Pn+1-|X|).

Если оба операнда отрицательны X<0, Y<0, то количественный эквивалент кода значащих разрядов произведения получится равным

(Pn − X )(Pn − Y ) = P2n − Pn X − Pn Y + X Y . (1-11)

Так как произведение положительно, правильный код значащих разрядов произведения должен иметь количественный эквивалент X Y .

Ошибка составит величину

X Y - (P2n − Pn X − Pn Y + X Y ) = Pn X + Pn Y − P2n . (1-12)

Что следует сделать для ликвидации ошибок?

Очевиден первый вариант ответа на этот вопрос – устранять последствия неправильных действий - устранять ошибку путем ее компенсации. В данном случае этот путь поиска вполне реален, так как ошибка детерминирована. Ее можно устранять путем прибавления той или иной корректирующей поправки к результату умножения. Величина корректирующей поправки зависит от знаков операндов.

При несовпадении знаков операндов достаточно прибавить к коду результата умножения сдвинутый влево на n разрядов код дополнения положительного операнда до Pn+1 для того, чтобы количественный эквивалент (1-8) кода результата умножения стал равным количественному эквиваленту правильного результата (1-9). Действительно, если, например X<0, а Y≥0, то ошибочный результат (1-8) увеличенный на (1-10) будет равен

(Pn − X )Y + Pn (Pn+1 − Y ) = P2n+1 − XY ,

что и требуется.

Если знаки обоих операндов отрицательны, то к результату умножения достаточно прибавить сдвинутые на n разрядов влево значащие разряды прямых кодов операндов и уменьшить результат на единицу в разряде 2n. Это приведет к тому, что количественный эквивалент результата станет равным требуемому. Действительно, прибавив к ошибочному произведению (1-11) ошибку (1-12) получим:

(P2n − Pn X − Pn Y + X Y ) + (Pn X + Pn Y − P2n ) = X Y .

Пример 16. Пусть десятичные операнды X=±910,24; Y=±800,13. Правильные значения произведений XY=±728310,3312. Дополнительные коды операндов 0 910.24; 1 089.76 и 0 800.13; 1 199.87 соответственно. Дополнительные коды произведений 0 0728310,3312 и 1 9271689.6688.

Перемножим дополнительные коды операндов по правилу умножения в прямых кодах и введем корректирующие поправки.

		0 910.24	1 089.76	1 089.76
		1 199.87	0 800,13	1 199.87
		181929.6688	071819.6688	017940.3312
		908976	919987	091024
		1 9271689.6688	1 9271689.6688	080013

Здесь n=3	1
Pn(Pn+1-|X|)=103(104-910.24)=9089760	0 0728310.3312

Висходных данных отсутствуют значения поправок. Поэтому их приходится вычислять путем взятия дополнений операндов, что сильно осложняет процесс умножения.

4.5.Операция алгебраического деления

Вотличие от умножения, сложения и вычитания результат операции деления в общем случае не может быть представлен точно в формате конечной длины. Поэтому различают

•Деление целых с вычислением целого частного и/или остатка.

•Деление целых и действительных чисел с вычислением частного в заданном формате с фиксированной точкой.

•Деление целых и действительных чисел с вычислением заданного количества значащих разрядов частного.

•Деление целых и действительных чисел с вычислением заданного количества

значащих разрядов частного с округлением результата.

Знак частного равен сумме по модулю 2 знаковых разрядов операндов.

Операнды могут быть числами со знаком или без знака. При делении целых без знака принимают, что знак операндов положителен, а знаки частного и остатка отбрасывают.

Особые случаи. При делении возникают особые случаи, когда оба или один из операндов равны нулю. Пусть X – делимое, Y - делитель, Z – частное, R – остаток.

X=0; Y≠0. Результат Z=0 и R=0. Вопрос состоит в знаках результата

1.X ≠0; Y=0. Частное Z=∞ и не является конкретной числовой величиной. Открыт вопрос об остатке R и о знаках частного и остатка.

2.X=0; Y=0. Частное Z и остаток R не являются числовыми величинами. Поэтому при делении обязательно проверяют операнды на нуль. При обнаружении

особого случая процесс деления прерывают и формируют признак особого случая. Принимают решение о том, что делать дальше. Обычно частному и остатку присваивают нулевые значения. Знак частного определяют как сумму по модулю 2 знаковых разрядов операндов, а знак остатка принимают равным знаку делимого. В случаях 1 и 2 процесс вычислений прерывают.

Рассмотрим результаты различных операций деления при отсутствии особых случаев.

Деление целых с вычислением целого частного Z и целого остатка R.

При любом способе деления целых с вычислением целого частного и остатка в любой системе счисления результаты должны быть точными и удовлетворять отношению

X=YZ+R, (14)

причем R≤Y -1.

Формат частного должен быть равен формату делимого, так как при Y=1, частное

Z=X.

Формат остатка должен быть равен формату делителя, так как модуль остатка может быть меньше модуля делителя всего лишь на 1.

Знак остатка совпадает со знаком делимого. Действительно, из (14) следует, что при X<0, произведение YZ<0. Поэтому для вычисления делимого по (14) нужно к отрицательной величине YZ прибавлять отрицательный остаток.

Например, 16:3=+5 и R=+1; 16:(-3)=-5 и R=+1; (-16):3=-5 и R=-1; (-16):(-3)=+5 и

R=-1.

Деление целых и действительных чисел с вычислением частного в формате с фиксированной точкой.

Частное Z вычисляют с абсолютной погрешностью ∆=X/Y-Z, величина которой неизвестна, а ее значение принадлежит некоторому заданному интервалу

[∆макс, ∆мин], причем знак ∆ может любым, если ∆макс≥0, а ∆мин<0. Так, что

X=YZ+Y∆. (15)

Формат частного выбирают исходя из границ интервалов, которым могут принадлежать абсолютные значения операндов. Очевидно, что формат частного должен позволять сохранять значение старшего значащего разряда частного.

Так как

Z макс= X макс/Y мин, (1-16)

то, зная X макс и Y мин, не трудно найти вес старшего значащего разряда в формате Z. Количество значащих разрядов в формате выбирают исходя из заданной точности

представления и выбранного способа округления Z (см. раздел тт ).

Деление целых и действительных чисел с вычислением заданного количества значащих разрядов частного.

Результатами являются точные значения заданного количества l старших значащих разрядов частного, начиная с первого разряда слева не равного нулю, и индекс i младшего значащего разряда. Например, при l=5 результат деления 15,3:(-17,1)=-0,89473684…

должен быть (Z=-89473; i=-5).

В особом случае при X=0 и Y≠0 следует всем значащим разрядам частного присвоить значение 0, принять i=0 и сформировать признак особого случая.

Формат частного включает разряд знака и l значащих разрядов. Формат i целого со знаком выбирают исходя из значений индекса младшего разряда минимально возможного значения частного при заданных форматах операндов и значения l.

Так как младшие разряды частного отбрасываются (их количество в общем случае бесконечно велико), то образуется ошибка в его представлении. Абсолютная погрешность частного ∆=X/Y-Z при таком его вычислении в точности равна количественному эквиваленту не вычисленных младших разрядов или, это то же самое, количественному эквиваленту R/Y

∆=R/Y, (17)

где R – последний остаток от деления. Справедливы отношения

X=YZ+Y∆=YZ+R. (18)

Знак абсолютной погрешности ∆ не является случайным, а совпадает со знаком частного, так как знак R совпадает со знаком делимого.

Модуль абсолютной погрешности частного случаен и его величина

∆ <P i,

(1-19)

где P – основание системы счисления;

i≠const – индекс младшего разряда частного, который определяется вычисляемым в процессе деления положением запятой в частном.

Максимальное значение модуля погрешности можно принять

∆ макс≈P i. (1-20)

Относительная погрешность, приведенная к величине частного

δ≈∆/Z, (1-21)

всегда положительна, так как знак погрешности ∆ совпадает со знаком частного. Максимальное значение относительной погрешности зависит только от основания

системы счисления и от количества вычисляемых разрядов в частном

δмакс≈∆макс/Zмин= ∆ макс/ Z мин=P i/P i+l-1= P -(l-1), (1-22)

так как Z мин содержит только одну 1 в старшем значащем разряде с индексом i+l-1.

Деление целых и действительных чисел с вычислением заданного количества значащих разрядов частного с округлением результата.

Отличается от предыдущего случая тем, что с целью уменьшения погрешности результат округляется до ближайшего к точному значению частного.

Рассмотрим некоторые способы вычисления разрядов частного и остатка.

Деление действительных чисел можно свести к делению целых. Для этого следует в дробных частях операндов уровнять количество разрядов, приписав, справа к одному из них недостающие нули, и интерпретировать полученные коды как целые. Например, 53,253:2,4=53,253:2,400=53 253:2 400. Поэтому в дальнейшем будем рассматривать способы деления целых.

Деление прямых двоичных кодов операндов с вычислением прямых кодов частного и остатка.

Знаки частного и остатка определяют по приведенным выше правилам и сводят деление к вычислению значащих разрядов частного и остатка по значащим разрядам операндов.

В основу способов деления могут быть положены следующие результаты.

Пусть делимое X>0 и делитель Y>0 двоичные n разрядные целые. Справедливо отношение

X =YZ + Rm , (23)

где Z – частное, индекс старшего значащего разряда которого не может превышать n-

1;

Rm – остаток от деления X на Y;

m – индекс младшего разряда частного (m ≤ n-1). Остаток должен удовлетворять условию 2m(Y-1) ≥ Rm ≥ 0.

n−1

Поскольку частное Z = ∑2i zi , где zi - цифры частного Z и zi {0,1}, то из (23)

m

следует

(1−30)

(1− 27) (1− 28)

n−1

X =Y ∑2i zi + Rm . (24)

m

Из (24) следует

X = 2n−1Yzn−1 + Rn−1 ;

Rn−1 = 2n−2Yzn−2 + Rn−2 ;

R	= 2n−3Yz	+ R	;			(25)
n−2	n−3	n−3
			………………..
			R	= 2mYz	+ R	,
			m+1	m	m

где Ri - промежуточный остаток (i=n-1, n-2, … , m), причем 2i(Y-1) ≥ Ri ≥ 0. Из (25) получим

R	= X	− 2n−1Yz		n−1	;
n−1
R	= R		− 2n−2Yz		n−2	;
n−2	n−1						(26)
...................................

Rm = Rm+1 − 2m Yzm.

Так как члены выражения (26) не меньше нуля и zi {0,1}, то из (26) следуют

правила для вычисления остатков и значений разрядов частного, начиная со старшего разряда zn-1:

i = n −1, n − 2, ... , m;

Rn = X ;

	при Ri +1 − 2	i	Y ≥ 0,
1					(1	− 29)
zi =			i
	при Ri +1 − 2			Y < 0;
0

Ri = Ri +1 − 2i Yzi .

Выражение (1-29) можно представить в иных формах:

X=27

X1 Y=5 00011011 101

101 00101.011

(X1≥Y)=0

00110110

101

(X1≥Y)=0

01101100

101

(X1≥Y)=1

00111000

0101

(X1≥Y)=0

01110000

101

(X1≥Y)=1

01000000

101

(X1≥Y)=0

10000000

101

(X1≥Y)=1

01100000

101

(X1≥Y)=1

z	i	= ¬sign(R		−2i Y );	(1−31)
			i+1
z = (R			≥ 2i Y ).		(1−32)
	i	i +1

На основании полученных правил могут быть разработаны различные способы их реализации. Рассмотрим некоторые из них.

Деление чисел с просмотром разрядов делимого слева направо.

Пусть делимое X>0 и делитель Y>0 двоичные целые без знака в форматах включающих n и k разрядов соответственно. Индекс старшего значащего разряда частного должен совпадать с индексом старшего разряда делимого и быть равным n-1. Индекс младшего разряда частного m определяется требуемым числом разрядов в частном и может быть m≤n.

Разряды частного, начиная с zn-1 до zm включительно, вычисляют придерживаясь выражений (31), (32), но для упрощения и/или ускорения вычислений вводят различные модификации не влияющие на результат.

Деление с записью очередного сдвинутого влево остатка на место предыдущего и вычислением разряда частного в соответствии с (32).

Рассмотрим способ деления на примере.

00100000

Пример 25. Пусть X=110112=2710; Y=1012=510. Количество разрядов в делимом n=5; в делителе – k=3. Индексы старших разрядов частного и делимого равны n-1=4, так как при Y=1 Z=X. Вычислим разряды частного от z4 до z-3. Тогда m=-3; i =4,3, ... ,-3.

Из (32) следует, что о значении разряда zi (i =n-1, n-2, … ,m) можно судить, сравнивая предыдущий остаток Ri+1 с делителем, сдвинутым при i >0 на i разрядов влево, а при i<0 на i разрядов вправо. При i=n-1 остаток Ri+1=Rn=X, а делитель сдвинут на n-1 разрядов влево так, что младший значащий разряд делителя совмещен со старшим разрядом делимого в одной позиции.

Из (30) следует, что при zi=0 очередной остаток Ri равен предыдущему, а при zi=1 очередной остаток равен Ri+1-2iY.

Исходя из сказанного, выполним следующие действия. Расширим формат делимого, приписав к нему слева k нулей.

Разобьем формат расширенного делимого на две группы разрядов, старшую и младшую. К старшей группе (обозначим ее X1) отнесем k+1 разрядов.

Деление будем выполнять по шагам.

“Наймем работников”, которые действуя одновременно и параллельно будут в каждом шаге выполнять каждый свою работу

1.Сравнивать количественные эквиваленты X1 и Y, вычисляя значение отношения X1≥Y. Сравниваются (k+1)-разрядный код X1 с k-разрядным кодом Y.

2.Вычислять значение разности X1-Y.

Вкаждом шаге результат сравнения является очередной цифрой частного, начиная со

старшей.

Результат вычисления разности X1-Y служит для определения очередного остатка и используется только в том случае, когда отношение (X1≥Y)=1, т.е. при X1-Y≥0. Поэтому можно разрешить: выполнять вычитание с ошибкой при X1<Y; вычислять только k младших разрядов разности X1-Y. Это позволит упростить и ускорить выполнение операции вычитания.

Вшаге образуем новое делимое по следующему правилу. Если цифра частного 0, сдвинем делимое влево на один разряд с занесением нуля справа и потерей старшего разряда. Сдвиг сводится к чтению делимого и последующей записи его значения на прежнее место со смещением влево. Если цифра частного 1, выполним ту же работу, но при записи подменим старшие k разряды вычисленной разностью.

Действительно. При zi=0 очередной остаток Ri равен предыдущему (30). Из (32) и (30) следует, что в очередном шаге следует повторить вычисления, сдвинув делитель на один разряд вправо по отношению к его положению в предыдущем шаге или, это то же самое, сдвинув делимое на разряд влево. При zi=1 младшие разряды очередного остатка совпадают

смладшими разрядами предыдущего остатка не участвовавшими в вычислениях, а старшие -

равны разности вычисленной вторым работником. Поэтому при zi=1 для получения очередного делимого нужно сдвинуть старое делимое на разряд влево с одновременной заменой старших разрядов вычисленной разностью. Поскольку при сдвиге старший разряд разности будет потерян, то нет смысла его вычислять, что учтено при вычислении X1-Y.

Ваппаратуре можно новое делимое записывать на место старого. Это позволяет использовать в очередном шаге оборудование, использовавшееся для сравнения и вычисления нового делимого в предыдущем шаге.

Впримере 25 в первом шаге первый работник вычислит (X1≥Y)=0 - старшую цифру частного. Результат работы второго работника не нужен. Одновременно с записью цифры

частного 0, сдвинем делимое влево. Получим новое делимое X=00110110 и X1=0011. Во втором шаге результат сравнения 0. Очередное делимое X=01101100 и X1=0110. В третьем шаге цифра частного 1, так как (X1≥Y)=1. Разность X1-Y=001. Заменив, старшие три разряда в сдвигаемом делимом на разность получим очередное делимое 00111000.

Процесс деления может продолжаться до бесконечности. Для прекращения процесса используют следующие правила:

− При делении целых с вычислением целого частного и остатка выполняют n шагов. Искомый остаток имеет формат делителя и размещен в старших разрядах делимого вычисленного в последнем шаге. В примере 25 он выделен жирным шрифтом и равен 010.

−При делении целых и действительных чисел с вычислением частного в заданном формате с фиксированной точкой шаги выполняют до заполнения всех разрядов формата частного.

−При делении целых и действительных чисел с вычислением заданного количества значащих разрядов частного выполняют отсчет числа выполненных шагов, начиная с шага результатом которого является первая единица в частном, и продолжают выполнять шаги до тех пор, пока количество отсчитанных шагов не станет равным заданному количеству значащих разрядов.

Операцию вычитания можно заменить сложением X1 с дополнением Y. Например, в примере 25 дополнение 101 будет равно 011. Значения суммы будут использоваться только

при (X1≥Y)=1 и только k ее младших разрядов, что позволит упростить выполнение операции сложения. Убедитесь самостоятельно, что от такой замены результат вычисления не изменится.

Деление в дополнительных кодах с получением частного в дополнительном коде.

Если операнды представлены в дополнительном коде, можно преобразовать их в прямой код, затем выполнить деление в прямом коде и, если частное должно быть представлено в дополнительном коде, преобразовать прямой код частного в дополнительный. Процедуры преобразования кодов замедляют процесс деления. Поэтому применяют способы деления без промежуточного преобразования операндов в прямой код.

При конструировании способов деления в дополнительных кодах можно в их основу положить рассмотренные способы деления в прямых кодах. Очевидно, что знак дополнительного кода частного можно вычислять так же как в прямом коде сложением по модулю 2 знаковых разрядов операндов. Следовательно, задача сводится к поиску способа деления значащих разрядов операндов представленных в дополнительном коде.

При расширении формата делимого влево следует копировать в дополнительные разряды знаковый разряд делимого, чтобы не изменить его количественный эквивалент. Например, делимое x=1 00101=-27. После расширения формата делимого на два разряда влево x=1 1100101=-27.

Сконструируем способ деления в дополнительных кодах, положив в его основу способ деления в прямых кодах использованный в примере 25, допуская его модификацию. Заметим, что многие из рассматриваемых в конструируемом способе решений могут быть применены при конструировании иных способов деления в дополнительном коде.

При делении в прямых кодах для нахождения очередной цифры частного определяли: укладывается ли делитель в коде X1 старших разрядов делимого, относя к ним столько разрядов делимого, какова длина делителя. При делении в дополнительном коде можно поступать аналогично. Остается лишь открытым вопрос о том, как выполнять сравнение модулей чисел со знаком, если они представлены в дополнительном коде.

Если знаки операндов совпадают, то судить о том, укладывается ли в x1 делитель можно по знаку их разности. Например, +7–(+5)=+2 (укладывается); -7–(-5)=-2 (укладывается). Если знаки операндов не совпадают, то соответствующим признаком является знак суммы. Например, +7+(-5)=+2 (укладывается); -7+(+5)=-2 (укладывается).

Следовательно, если знаки операндов совпадают, для сравнения следует вычислять разность x1-y; если знаки операндов не совпадают, следует выполнять сложение x1+y. Признаком укладывания в обоих случаях является совпадение знака результата сложения или вычитания со знаком делимого.

	A					B					C							D
X=0 11011д=+27					X=1 00101д=-27					X=1 00101д =-27							X=0 11011д=+27
X1		Y=0 101д=+5			X1		Y=1 011д=-5			X1			Y=0 101д=+5				X1	Y=1 011д=-5
00011011		0101			11100101		1011			11100101			0101				00011011			1011
0101		000101.011обр			1011		000101. 011обр			0101							1011
													111010.100обр							111010.100 обр
1100					0011					0011							1100
00110110					11001010					11001010							00110110
0101					1011					0101							1011
1110					0001					0001							1110
01101100					10010100					10010100							01101100
0101					1011					0101							1011
0001					1110					1110							0001

Заметим, что можно предложить иные способы сравнения.

Из приведенных примеров сравнения видно, что признаком 1 в прямом коде частного будет совпадение знака делимого со знаком разности или суммы. Для получения обратного кода частного можно использовать признак совпадения знака делителя со знаком разности (суммы) как признак 1 в разряде частного. Дополнительный код частного можно получить преобразованием его обратного кода в дополнительный.

Если делитель не укладывается в X1, для получения очередного значения X1 следует сдвинуть делимое на один разряд влево с потерей разряда слева и занесением нуля справа (удвоить). В противном случае, нужно при сдвиге делимого на разряд влево заместить его старшие разряды вычисленной разностью (суммой). Рассмотрим применение этого правила на примере.

4.6.Операция округления действительных чисел

При выполнении операций над действительными числами может быть получен результат, не умещающийся в разрядную сетку, отведенную для хранения результата. Так как операнды действительные числа и, следовательно, представлены с некоторой погрешностью, результат не может быть точным. Поэтому с целью размещения результата в разрядной сетке он может быть округлен.

Округление до нуля. Это простейший способ округления не требующий никаких затрат на реализацию. Он состоит в отбрасывании младших разрядов результата не умещающихся в разрядной сетке.

Рассмотрим особенности этого способа при кодировании чисел в прямом, обратном и дополнительном коде.

Из (2) следует, что количественный эквивалент прямого кода числа до округления можно представить как сумму количественных эквивалентов сохраняемых старших разрядов от n до k и отбрасываемых младших разрядов от k-1 до m

n−1	k −1
Nпр = (−1)an ∑ai Pi + (−1)an ∑ai Pi ; an {0,1}.
k	m

Результат округления будет иметь количественный эквивалент

a n−1

Nпро = (−1) n ∑ai Pi ,

k

а абсолютная погрешность округления

a k −1

∆про = (−1) n ∑ai Pi

m

имеет знак, совпадающий со знаком результата. Модуль абсолютной погрешности 0≤ ∆про <Pk меньше веса младшего разряда сохраняемого результата.

Если данное представлено в обратном коде, то до округления его количественный эквивалент из (4)

n −1

Nобр = −an (Pn − Pm ) + ∑ai Pi .

m

После округления до k>m разряда путем отбрасывания k-m младших разрядов

n−1

Nобро = −an (Pn − Pk ) + ∑ai Pi .

k

Тогда ошибка округления обратного кода путем отбрасыванием младших разрядов составит

k −1

∆обро = Nобр − Nобро = −an (Pk − Pm ) + ∑ai Pi . m

Знак ошибки, так же как при округлении до нуля в прямом коде, совпадает со знаком числа, и ее модуль 0≤ ∆обро <Pk меньше веса младшего разряда сохраняемого результата.

Округление до нуля дополнительного кода числа приводит к иным результатам. Из (1-3) следует, что до округления количественный эквивалент дополнительного

кода

n−1

Nдоп = −an Pn + ∑ai Pi .

m

После округления до k>m разряда путем отбрасывания k-m младших разрядов

n−1

Nдопо = −an Pn +∑ai Pi .

k

Ошибка округления до нуля дополнительного кода составит

k −1

∆допо = Nдоп − Nдопо = ∑ai Pi . m

Следовательно, знак ошибки не зависит от знака числа, а ее модуль меньше веса младшего разряда сохраняемого результата.

Чтобы получать после округления дополнительного кода отрицательного числа результат с количественным эквивалентом таким же, как и при округлении этого числа в прямом коде, необходимо увеличить результат усечения на 1 его младшего разряда кроме случая, когда отбрасываемые разряды равны нулю.

Пример 31. В примерах A,B,C выполнено округление до нуля отрицательного десятичного числа в прямом, обратном и дополнительном коде.

A	B		C	D	E	F	G		H	I
1|2.43470пр= 1|7.56529обр=1|7.56530доп				1|2.43000пр =1|7.57000доп		1|1.10011пр = 1|0.01100обр= 1|0.01101доп 1|0.010доп
1|2.43пр	= 1|7.56обр	≠ 1|7.56доп		1|2.43пр	= 1|7.57доп	1|1.10пр	= 1|0.01 обр ≠	1|0.01доп		1|0.01доп
		+	1					+	1
		1|7.57доп						1|0.10доп

Впримере C результат усечения дополнительного кода 1|756доп является ближайшим меньшим приближением к исходному числу. Чтобы получить дополнительный код ближайшего большего приближения выполнено прибавление 1 к младшему разряду.

Примеры D и E иллюстрируют тот факт, что при равенстве нулю отбрасываемых разрядов дополнительного кода отрицательного числа не следует прибавлять 1 к младшему разряду усеченного кода.

Впримерах F,G,H,I выполнено округление до нуля двоичных кодов. Систематическое одностороннее смещение промежуточных результатов вычислений

влечет накопление ошибок и снижает достоверность конечного результата, что является существенным недостатком этого способа округления.

Округление до нуля с увеличением на 1 цифры в младшем сохраняемом разряде, если ее количественный эквивалент меньше половины количественного эквивалента основания системы счисления. Например, при P=10 цифра в сохраняемом разряде k остается без изменения, если ak {5,6,7,8,9}, и заменяется на большую, если ak {0,1,2,3,4}. Разряды от m до k-1 отбрасываются. В двоичной системе цифра ak=1 сохраняется, а цифра ak=0 заменяется на ak=1.

Если при округлении ak сохранит значение, то погрешность округления будет такой же, как и при округлении до нуля. Если ak возрастет на 1, то погрешность изменит свой знак, а ее модуль не превысит веса сохраняемого разряда. Поскольку до округления значения ak

равновероятны, знак погрешности равновероятен. Равновероятно ее значение в интервале

Pk>∆о1>-Pk.

Рассматриваемый способ округления не намного сложнее предыдущего, так как прибавление 1 не может вызвать распространения переноса. Равно вероятность погрешности на интервале Pk>∆о1>-Pk препятствует накоплению погрешности округления. Недостатки этого способа в том, что интервал, в котором лежит погрешность, вдвое больше, чем при способе округления до нуля, и, кроме того, результат после округления не может содержать 0 в младшем разряде. Последнее может приводить к существенным ошибкам в вычислениях. Например, многократное деление переменной на основание системы счисления с округлением никогда не приведет к результату равному нулю.

Округление до ближайшего числа, которое можно представить в сокращенной разрядной сетке.

Исходный код заменяется укороченным кодом, количественный эквивалент которого является ближайшим к количественному эквиваленту исходного кода. Если существуют два равноценных ближайших укороченных кода, то возникает особый случай. В особом случае, если цифра младшего разряда кода полученного округлением до нуля ak<P/2, то для замены выбирают результат округления до нуля. В противном случае к младшему разряду результата округления до нуля прибавляют 1 и тем самым заменяют исходный код другим ближайшим значением.

4.7. Особенности представления информации в ПК

Числовая информация внутри ПК кодируется в двоичной или в двоично-десятичной системах счисления; при вводе и выводе любой информации используются специальные коды представления информации — коды ASCII, эти же коды применяются для кодирования буквенной и символьной информации и внутри ПК.

Для удобства работы введены следующие термины для обозначения совокупностей двоичных разрядов (табл.5.1.). Эти термины обычно используются в качестве единиц измерения объемов информации, хранимой или обрабатываемой в компьютере.

		Таблица 5.1.
Количество двоичных разрядов в группе		Количество двоичных разрядов в группе
1		Бит
8		Байт
16		Параграф
8	• 1024	Кбайт (килобайт)
8	• 102422	Мбайт (мегабайт)
8	• 102423	Гбайт (гигабайт)
8	• 102424	Тбайт (терабайт)

Последовательность нескольких битов или байтов часто называют полем данных. Биты в числе (в слове, поле и т. п.) нумеруются справа налево, начиная с 0-го

разряда. В ПК могут обрабатываться поля постоянной и переменной длины. Поля постоянной длины:

•слово — 2 байта;

•двойное слово — 4 байта;

•полуслово — 1 байт;

•расширенное слово — 8 байтов.

Числа с фиксированной запятой чаще всего имеют формат слова и полуслова; числа с плавающей запятой — формат двойного и расширенного слова (математические сопроцессоры IBM PC могут работать с 10-байтными словами).

Поля переменной длины могут иметь любой размер от 0 до 255 байтов, но обязательно равный целому числу байтов.

Двоично-кодированные десятичные числа могутбыть представлены в ПК полями переменной длины в так называемых упакованном и распакованном форматах. В упакованном формате для каждой десятичной цифры отводится по 4 двоичных разряда (полбайта), при этом знак числа кодируется в крайнем правом полубайте числа (1100 — знак

«+» и 1101 — знак «-»).

Упакованный формат используется в ПК обычно при выполнении операций сложения и вычитания двоичнодесятичных чисел.

В распакованном формате для каждой десятичной цифры выделяется по целому байту, при этом старшие полубайты (зона) каждого байта (кроме самого младшего) в ПК заполняются кодом 0011 (в соответствии с ASCII-кодом), а в младших (левых) полубайтах обычным образом кодируются десятичные цифры. Старший полубайт (зона) самого младшего (правого) байта используется для кодирования знака числа.

Распакованный формат используется в ПК при вводе-выводе информации, а также при выполнении операций умножения и деления двоично-десятичных чисел.

Код ASCII (American Standard Code for Information Interchange — американский стандартный код для обмена информацией) имеет основной стандарт и его расширение. Основной стандарт для кодирования символов использует шестнадцатеричные коды 00-7F, расширение стандарта — 80-FF.

Основной стандарт является международным и применяется для кодирования управляющих символов, цифр, знаков пунктуации, букв латинского алфавита и других символов; в расширении стандарта кодируются символы псевдографики и буквы национального алфавита (естественно, в разных странах разные). Пользоваться таблицей достаточно просто. Следует приписать шестнадцатеричную цифру номера строки справа к шестнадцатеричной цифре номера столбца. Так получится шестнадцатеричный код символа.

Любой символ, представленный в таблице на рис. 3.5, при работе в DOS может быть введен в ПК с клавиатуры набором его десятичного кода (соответствующего шестнадцатеричному ASCII-коду) на малой цифровой клавиатуре при нажатой клавише Alt.

Наряду с кодом ASCII в ВС, в частности в сети Интернет, используется общий для всех стран мира универсальный код — Unicode. Этот код основан на паре байтов — машинном слове. Шестнадцати битов хватает для отображения 65 535 знаков.

Такого количества достаточно для всех существующих алфавитов (то есть алфавиты большинства стран мира размещаются в основном стандарте этого кода).

Лекция 5

Логические основы цифровой техники

5.1. Элементы алгебры логики

Алгебра логики — это раздел математической логики, значение всех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1.

Алгебра логики оперирует с логическими высказываниями. Высказывание — это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом считается, что высказывание удовлетворяет закону исключенного третьего, то есть каждое высказывание или истинно, или ложно, и не может быть одновременно и истинным и ложным.

В алгебре логики все высказывания обозначают буквами а, b, с и т. д. Содержание высказываний учитывается только при введении их буквенных обозначений, и в дальнейшем над ними можно производить любые действия, предусмотренные данной алгеброй. Причем если над исходными элементами алгебры выполнены некоторые разрешенные в алгебре логики операции, то результаты операций также будут элементами этой алгебры.

Простейшими операциями в алгебре логики являются операции логического сложения (иначе: операция ИЛИ (OR), операция дизъюнкции) и логического умножения

(иначе:1 операция И (AND), операция конъюнкции). Для обозначения операции логического сложения используют символы + или V> a логического умножения — символы • или ^. Правила выполнения операций в алгебре логики определяются рядом аксиом, теорем и следствий. В частности, для алгебры логики применимы следующие законы.

1. Сочетательный:

(а + Ь) + с = а + (Ь + с), (а • Ь) • с = а • (Ь • с).

2. Переместительный:

(а + 6) = (Ь + а), (a-b) = ( b - a).

3. Распределительный:

а • (Ь + с) = а • b + a • с, (а + Ь) • с = а • с + Ь • с.

Справедливы соотношения, в частности:

а + а = а, a + b = b, если а < Ь,

а-а = а, а-Ъ-а, если а < Ь,

a+ a-b = a, a- b = Ь, если а > Ь,

а+ Ь = а, если а > Ь,

а+ b = b, если а < Ь.

Наименьшим элементом алгебры логики является 0, наибольшим элементом — 1.

В алгебре логики также вводится еще одна операция — отрицания (операция НЕ, инверсия), обозначаемая чертой над элементом.

По определению:

а + (-a) = 1 а • (-а) = 0, -0 = 1, -1=0.

Функция в алгебре логики — выражение, содержащее элементы алгебры логики а, Ь, с и др., связанные операциями, определенными в этой алгебре.

Примеры логических функций:

f(a,b,c) = -a + a-b -c + a + c, f(a, b,c) = a-b +b-c + -(a-b-c).

Согласно теоремам разложения функций на конституэнты (составляющие), любая функция может быть разложена на конституэнты 1:

f(а) = f(1)• а + f(0) • (-a) f(a,b) = f(1,b) • a + f(0,b) • (-a) =

= f(1,1) • a • b + f(1,0) • a(-b)+f(0,1) • (-а) • b + f(0,0) • (-а) • (-b)

и т. д.

Эти соотношения используются для синтеза логических функций и вычислительных

схем.

5.2. Методы анализа и синтеза комбинационных схем

Техническим аналогом булевой функции в вычислительной технике является, так называемая, комбинационная схема, на вход которой поступают и с выхода снимаются электрические сигналы в виде одного из уровней напряжения, соответствующих значениям логического 0 и логической 1.

Для выяснения, что же такое комбинационная схема, рассмотрим схему S, имеющую m входов и n выходов (рис. 1). На её входы могут быть поданы наборы значений

входных	переменных Xi {0,1}, i =			1,m	, а на выходах формируются выходные переменные
	j =		.
Yj {0,1},		1,n

	X1
	X2
		.
		.
	Xm	.

S

Y1

. Y2

.

.

Yn

Рис. 1

Схема S называется комбинационной, если каждую из n функций её выходов Y1,Y2, ..., Yn можно представить как булеву функцию входных переменных X1, X2, ..., Xm.

Комбинационная схема описывается с помощью системы уравнений (1), где Fi – булева функция.

Y1	= F1 ( X1 , X 2 ,...., X m )			(1)
Y2	= F2 ( X1 , X 2 ,..., X m )
....................................
Yn	= Fn ( X1 , X 2 ,..., X m )
Как следует из определения комбинационной схемы, значения выходных переменных
Yj в произвольный момент времени		однозначно	определяются значениями входных
переменных Xi.
Структурно комбинационная схема		может быть	представлена как совокупность
элементарных логических схем – логических элементов (ЛЭ).				ЛЭ выполняют над входными
переменными элементарные логические операции типа И-НЕ,				И, ИЛИ, ИЛИ-НЕ и т.д. Число

входов логического элемента соответствует числу аргументов воспроизводимой им булевой функции. Графическое изображение комбинационной схемы, при котором показаны связи между различными элементами, а сами элементы представлены условными обозначениями,

называется	функциональной схемой.
В ходе		разработки комбинационных		схем приходится		решать	задачи анализа и
синтеза.
Задача		анализа состоит в определении статических и динамических свойств
комбинационной		схемы.	В статике определяются		булевы	функции, реализуемые
комбинационной		схемой по известной ей структуре.			В динамике		рассматривается
способность	надёжного		функционирования	схемы в	переходных процессах при смене

значений переменных на входах схемы, т.е. определяется наличие на выходах схемы возможных нежелательных импульсных сигналов, которые не следуют непосредственно из выражений для булевых функций, реализуемых схемой.

Задача синтеза заключается в построении из заданного набора логических элементов комбинационной схемы, реализующей заданную систему булевых функций.

Решение задачи синтеза не является однозначным, можно предложить различные варианты комбинационных схем, реализующих одну и ту же систему булевых функций, но отличающихся по тем или иным параметрам. Разработчик комбинационных схем из этого множества вариантов выбирает один, исходя из дополнительных критериев: минимального количества логических элементов, необходимых для реализации схемы, максимального быстродействия и т.д. Существуют различные методы синтеза комбинационных схем, среди которых наиболее разработан канонический метод.

Канонический метод синтеза комбинационных схем.

Как отмечалось выше, комбинационная схема (КС) может иметь несколько выходов. При каноническом методе предполагается, что каждая выходная функция реализуется своей схемой, совокупность которых и даёт требуемую КС. Поэтому синтез сложной КС с n выходами заменяется синтезом n схем с одним выходом.

Согласно каноническому методу синтез КС включает в себя ряд этапов.

1.Подлежащая реализации булева функция (или её отрицание) представляется в виде СДНФ.

2.С использованием методов минимизации определяется минимальная ДНФ (МДНФ) или минимальная КНФ (МКНФ). Из полученных двух минимальных форм выбирается более простая.

3.Булеву функцию в минимальной форме согласно п.2 представляют в заданном (или выбранном разработчиком) базисе .

4.По представлению функции в заданном базисе строят комбинационную схему.

Простой конъюнкцией называется конъюнкция одной или нескольких переменных, при этом каждая переменная встречается не более одного раза (либо сама, либо ее отрицание).

Например, является простой конъюнкцией,

Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций.

Например, выражение является ДНФ.

Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма, у которой в каждую конъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одном и том же порядке.

Например,	выражение	является	ДНФ,	но	не	СДНФ.
Выражение		является СДНФ.

Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.

Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных, при этом каждая переменная входит не более одного раза (либо сама, либо ее отрицание).Например,

выражение	– простая дизъюнкция,
Конъюнктивной нормальной формой (КНФ) называется		конъюнкция простых дизъюнкций
(например выражение		– КНФ).

Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.

Например, выражение	является СКНФ.
Необходимо отметить, что подлежащая	реализации булева функция F(X1,X2,...,Xm)

может быть задана не на всех возможных наборах аргументов X1, X2, ..., Xm. На тех наборах, где функция неопределенна, её доопределяют так, чтобы в результате минимизации получить более простую МДНФ или МКНФ. При этом упростится и сама КС. Кроме того, довольно часто с целью получения ещё более простого представления функции МДНФ, полученная в п.2, представляется в так называемой скобочной форме, т.е. выносятся за скобки общие части импликант МДНФ.

Рассмотрим канонический метод синтеза на примере построения схемы полного одноразрядного двоичного сумматора.

Как известно из курса машинной арифметики, полный одноразрядный сумматор - это устройство, которое осуществляет сложение по mod 2 соответствующих разрядов (X1,X2) двоичных чисел с учётом переноса (Рm) в данный разряд из соседнего младшего разряда суммы. Сумматор вырабатывает цифру результата (S) в данном разряде и перенос (Рс) в соседний старший разряд суммы. Таблица истинности такого сумматора (т.е. представление булевой функции, которую он реализует, в виде СДНФ) представлена ниже.

	X1	0	0	0	0	1	1	1	1	Табл.1. Таблица истинности полного
	X2	0	0	1	1	0	0	1	1	одноразрядного двоичного сумматора.
	Pm	0	1	0	1	0	1	0	1
	S	0	1	1	0	1	0	0	1
	Pc	0	0	0	1	0	1	1	1

Необходимо получить булевы функции S=F1(X1,X2,Рm) и Рс=F2(X1,X2,Рm). Карты Карно для этих функций приведены ниже (рис.2).

X1	00	01	11	10
X2
Pm
0	0	1	0	1
1	1	0	1	0
Функция S

X1	X2	00	01	11	10
Pm
0		0	0	1	0
1		0	1	1	1
Функция PC

Рис.2. Карты Карно для функций S и Pc сумматора.

Как следует из приведённых карт, МДНФ соответствующих функций имеет вид:

S= X1

X 2

Pm+ X1

X2

P

+X1 X 2

P

+ X1 X2 Pm

(2)

m

m

Pc= X1 X2+X1 Pm+X2 Pm

Полученная система булевых функций представлена в базисе И, ИЛИ, НЕ. Соответствующая ей КС приведена на рисунке 4.

Полученную комбинационную схему можно упростить, вынеся за скобки общие части в выражениях для S и Рc, однако существенного результата это не даст (желательно самостоятельно в этом убедиться).

Значительно упростить схему можно, если воспользоваться другим базисом, например логическим элементом "ИСКЛЮЧАЮЩЕЕ ИЛИ". В этом случае выражение для S

можно записать S = (X1+X2+ Рm)mod2= X1 X2 Рm. Тогда схема для S будет иметь вид

(рис.3).

X1		=1			=1		S
X2
Pm

	Рис.3.
1.2.	Характеристики
комбинационных схем.

Сложность схемы оценивается количеством оборудования, составляющего схему. При разработке схем на основе конкретной элементной базы количество оборудования обычно измеряется числом корпусов (модулей) интегральных микросхем, используемых в схеме. В теоретических разработках ориентируются на произвольную элементную базу и поэтому для оценки затрат оборудования используется оценка сложности схем по Квайну.

Сложность (цена) по Квайну определяется суммарным числом входов логических элементов в составе схемы.

При такой оценке единица сложности – один вход логического элемента. Цена инверсного входа обычно принимается равной двум. Такой подход к оценке сложности оправдан по следующим причинам:

−сложность схемы легко вычисляется по булевым функциям, на основе которых строится схема: для ДНФ сложность схемы равна сумме количества букв,(букве со знаком отрицания соответствует цена 2), и количества знаков дизъюнкции, увеличенного на 1 для каждого дизъюнктивного выражения.

−все классические методы минимизации булевых функций обеспечивают

минимальность схемы именно в смысле цены по Квайну.

Практика показывает, что схема с минимальной ценой по Квайну обычно реализуется наименьшим числом конструктивных элементов – корпусов интегральных микросхем.

Быстродействие комбинационной схемы оценивается максимальной задержкой сигнала при прохождении его от входа схемы к выходу, т.е. определяется промежутком времени от момента поступления входных сигналов до момента установления

X1

&

1

S

X1

&

1

Pc

X 2

X2

X1

Pm

X1

X1

&

X2

X 2

X1

&

Pm

X2

Pm

Pm

Pm

X2

&

X1

Pm

&

X 2

X1

X1

&

X2

Pm

Рис.4. Функциональная схема комбинационного сумматора.

соответствующих значений выходных. Задержка сигнала кратна числу элементов, через которые проходит сигнал от входа к выходу схемы. Поэтому быстродействие схемы характеризуется значением rτ, где τ - задержка сигнала на одном элементе. Значение r определяется количеством уровней комбинационной схемы, которое рассчитывается следующим образом. Входам КС приписывается уровень нулевой. Логические элементы, связанные только со входами схемы относятся к уровню ПЕРВОМУ. Элемент относится к уровню k, если он связан по входам с элементами уровней k-1, k-2, и т.д. Максимальный уровень элементов r определяет количество уровней КС, называемое рангом схемы. Пример определения ранга r схемы приведён на рисунке 6.

уровень 0

уровень 1

уровень 2

уровень 3

X1

Y

&

&

1

X2

X3			1						r=3
X4
X5

Рис.6. Определение ранга схемы.

Как известно, любая булева функция может быть представлена в ДНФ, которой соответствует двухуровневая комбинационная схема. Следовательно, быстродействие любой КС в принципе можно довести до 2τ.

Минимизация булевой функции с целью уменьшения сложности схем обычно приводит к необходимости представления функций в скобочной форме, которой соответствуют схемы с r>2. Т.е., уменьшение затрат оборудования в общем случае приводит к снижению быстродействия схем.

Системы (серии) логических элементов и их основные характеристики.

При построении КС устройств вычислительной техники используются различные логические элементы, которые должны согласоваться по входным и выходным сигналам, напряжению питания и т.д. Для этой цели логические элементы объединяют в серии.

Серией (системой, комплексом) логических элементов ЭВМ называется предназначенный для построения цифровых устройств функционально полный набор логических элементов, объединяемый общими электрическими, конструктивными и технологическими параметрами, использующий одинаковый способ представления информации, одинаковый тип межэлементных связей. Система элементов чаще всего избыточна по своему функциональному составу, что позволяет строить схемы более экономичные по количеству использованных элементов.

Всостав серии входят элементы для выполнения логических операций, запоминающие элементы, элементы, реализующие функции узлов ЭВМ, а также специальные элементы для усиления, восстановления и формирования сигналов стандартной формы.

Конструктивно логические элементы представляют собой микроминиатюризованные интегральные электронные схемы (микросхемы), сформированные в кристалле кремния с помощью специальных технологических процессов.

Вбольшинстве современных серий элементов имеются микросхемы малой степени интеграции (ИС до 100 элементов на кристалл), средней степени (СИС – до 1000 элементов

на кристалл), большой степени интеграции (БИС – до 10000 элементов на кристалл) и сверхбольшой степени интеграции (СБИС – более 10000 элементов на кристалл). Логические элементы в виде ИС реализуют совокупность простых логических операций: И, ИЛИ, И-ИЛИ, И-НЕ, ИЛИ-НЕ и т.д. Логические элементы на СИС и БИС реализуют узлы ЭВМ, на СБИС – микроЭВМ.

Основными параметрами серии логических элементов являются:

-питающие напряжения и сигналы для представления логического 0 и логической 1;

-коэффициенты объединения по входу;

-нагрузочная способность (коэффициент разветвления по выходу);

-помехоустойчивость;

-рассеиваемая мощность;

-быстродействие.

Серия элементов характеризуется количеством используемых питающих напряжений и их номинальными значениями. Обычно логическому 0 соответствует низкий уровень напряжения, а логической 1 – высокий. Для наиболее часто используемых серий напряжение питания составляет +5В, уровень логической единицы 2,4-5В, уровень логического 0 – 0-0,4В.

Коэффициент объединения по входу (Коб) определяет максимально возможное число входов логического элемента, иными словами, функцию скольких переменных может реализовать этот элемент. Обычно Коб принимает значение от 2 до 4, реже Коб=8. Увеличение числа входов связано с усложнением схемы элементов и приводит к ухудшению других параметров – помехоустойчивости, быстродействия и т.д.

Коэффициент разветвления по выходу (Краз) показывает на сколько логических входов может быть одновременно нагружен выход данного логического элемента. Обычно Краз для наиболее часто используемых серий равен 10. Иногда вместо Краз задается предельно допустимое значение выходного тока логического элемента в состоянии 0 или 1.

Помехоустойчивость – это способность элемента правильно функционировать при наличии помех. Она определяется максимально допустимым напряжением помехи, при котором не происходит сбоя в его работе. Обычно это напряжение порядка 0,6-0,9 В.

Быстродействие логических элементов является одним из важнейших параметров и характеризуется временем задержки распространения сигнала. Этот параметр существенно зависит от технологии изготовления микросхем и лежит в диапазоне от единиц до сотен наносекунд.

Наиболее часто употребляемые типы интегральных микросхем – это потенциальные элементы транзисторно-транзисторной логики (ТТЛ) - серии К155, К555, К531, К1533 и т.д., транзисторной логики с эмиттерными связями (ЭСТЛ) – это серии К500,К1500, элементы на КМОП транзисторах - серии К176, К561,К564 и т.д.

При синтезе КС на реальных логических элементах необходимо обязательно учитывать ограничения на Коб и Краз.

СИНТЕЗ КС С УЧЕТОМ ОГРАНИЧЕНИЙ НА Краз .

При построении КС может оказаться, что выход k - го логического элемента нагружен n > Краз входов других ЛЭ (рис.7а). Это означает, что k - тый логический элемент

перегружен и необходимо принять меры, устраняющие указанное явление. Существуют два способа обеспечения заданногоКраз :

1.использование дополнительных развязывающих усилителей;

2.дублирование перегруженного элемента.

Схема с использованием дополнительных развязывающих усилителей представлена на рис.7.б. Количество p дополнительных усилителей, необходимых для обеспечения заданного Краз , определяется по формуле:

p > (n − Краз ) / (Краз − 1)

Недостаток рассматриваемого способа в том, что в цепь распространения сигнала вносится дополнительная задержка, что не всегда допустимо.

Схема с использованием дублирования перегружаемого элемента представлена на рис.7.в. Количество p дополнительных элементов, выполняющих ту же функцию, что и К-тый элемент, определяется по формуле:

p > Краз

При таком способе обеспечения Краз дополнительная задержка не вносится, но

увеличивается нагрузка на элементы, формирующие сигналы X1 и X 2 , что может привести

к перегрузке этих элементов и введению дополнительных элементов для обеспечения заданного Краз.

	&			&		X1
	k		Z1	1		X2
				&
	.		Z2
	.			2
	.
				.
				.
				&
			Zn
				n
		a)
	&			&
			Z1
	k1			1
				&
	.		Z2
	.			2
	.
				.
				.
				&
			Zk рз	kрз
	&			&
			Zn-p
	kp			1
				&
		. Zn-p+1
	.			2
	.
				.
				.
				&
		б)	Zn
				2

&1

k

1

.

.

.

	1
	2
.
.	.
.	.
	.

.

.

.

		&
Z1
		1
		&
Z2
		2
		.
		.
		&
Zk		kрз
рз
		&
Zkрз	+1	1
		&
Zkрз+2		2
		.
		.
		&
Z2kрз		kрз
		.
		.
		.
		&
Zn-1
		n-1
		&
Zn
		n

в)

Рис.7. Способы обеспечения требуемого Краз.

1.5. СИНТЕЗ КС С УЧЕТОМ ОГРАНИЧЕНИЯ НА Коб .

Как видно из полученной схемы для ее реализации необходимы элементы с K об = 2 или 3 (в отличие от исходной с K об = 4 или 5). Однако ранг схемы увеличился до 7, что приводит к увеличению задержки срабатывания схемы.

X 5

&

1

&

1

&

1

&

X 6

X

4

X 2

X

2

&

X 4

X 3

3

X

&

X

5

X 6

X 1

Рис. 8. Функциональная схема, полученная на основании факторного алгоритма.

1.6. Анализ комбинационных схем.

Задачи анализа КС возникают при необходимости проверить правильность синтеза (на этапе проектирования) или определить БФ, реализуемую КС (при анализе или ремонте схем). Все существующие методы анализа делятся на прямые и косвенные.

В результате анализа КС прямым методом получается множество наборов входных переменных, обеспечивающих заданное значение на выходе, что позволяет записать в алгебраическом виде БФ, реализуемую схемой. К прямым методам относится метод π- алгоритма.

Применение косвенных методов дает возможность определить реакцию схемы на заданный набор входных переменных в статике или проанализировать переходный процесс смены одного входного набора на другой. Примерами косвенных методов анализа, являются методы синхронного и асинхронного моделирования.

Для всех методов анализа необходимо описать схему в виде схемного списка, в который включается в общем случае следующие данные: номер ЛЭ в схеме; логическая функция, реализуемая ЛЭ; входные переменные для данного ЛЭ. Например, схема представленная на рис.9, может быть описана следующим списком:

X1

e1

e3

e4

Nэлем

Функция

Входы

&

&

1

X2

1

3

4

1

2И

X1 X2

X3

e2

2

2ИЛИ-НЕ

X3 X4

3

2И-НЕ

E1 E2

1

X4

2

4

2ИЛИ

E3 X5

X5

Рис. 9

1. 7 Анализ КС методом синхронного моделирования.

При данном методе считается, что все ЛЭ переключаются одновременно, без задержки. В результате применения метода определяется установившееся значение сигнала на выходе схемы.

Рассмотрим метод синхронного моделирования на примере схемы ( рис.9 ).

На первом этапе схему разбиваем на уровни и записываем в порядке возрастания уровня уравнения, описывающие функционирование ЛЭ:

	№уровня	№элемента	уравнение
	1	1	e1 = X1 IX2
		2
			e2 = X 3 + X 4
	2	3
			e3 = e1 Ie2
	3	4	Y = e4 = e3 + X5

Проанализируем схему при подаче на вход набора X1=0, Х2=0, Х3=0, Х4=1, Х5=1. Для этого решаем записанные уравнения в порядке возрастания уравнения. Имеем:

e1 = X1 I X 2 = 0 I0 = 0 ; e2 = X 3 + X 4 = 0 +1 = 0 ;

e3 = e1 I e2 = 0 I 0 =1 ;

Y = e4 = e3 + X 5 =1 +1 =1.

Следовательно, при подаче на вход набора {00011}, на выходе будет Y=1. Аналогично можно промоделировать работу схемы при подаче на вход любого другого набора.

1.9 Анализ КС методом асинхронного моделирования.

Реальный ЛЭ переключается за какое-то конечное время, зависящее от технологии изготовления, условий эксплуатации, емкостей нагрузки и т.д. Прохождение сигнала последовательно через несколько ЛЭ будет приводить к накоплению времени задержки и возникновению сдвига во времени выходного сигнала по отношению ко входному. Наличие задержки и порождаемого ею временного сдвига сигналов может приводить к появлению на выходе отдельных ЛЭ и всей схемы в целом кратковременных сигналов, не предусмотренных БФ, реализуемой схемой. Как иллюстрацию, рассмотрим схему рис.11, а .

X	1	e1
		1

&	e2 = Y
2

X

t1

e1

Y

t2

Рис. 11 . Статический риск сбоя. а)- схема, б)- временные диаграммы. t1-время задержки инвертора t2-время задержки элемента 2И

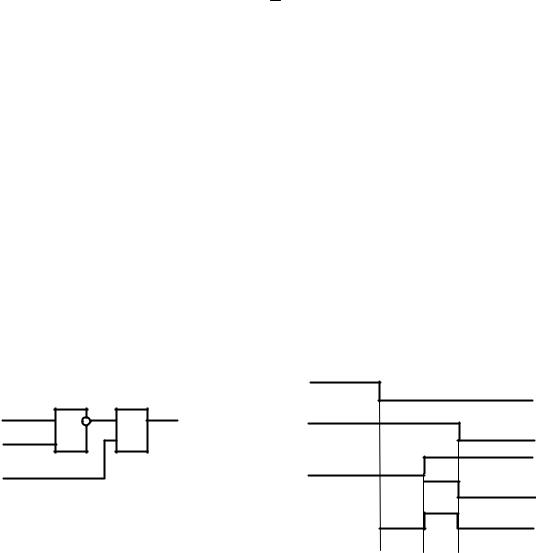
Данная схема реализует функцию Y = X I X = 0 , т.е. константу 0 независимо от

входного сигнала X. Однако в переходном процессе в результате задержки срабатывания ЛЭ возможна ситуация, когда на обоих входах элемента 2И будут логические единицы, что может привести к появлению на выходе схемы логической 1 (см. рис.11 б). Рассмотренный случай возможен при задержке срабатывания второго элемента больше, чем первого. Такое явление называется риском сбоя. Различают статистический и динамический риски сбоя.

При статическом риске сбоя до и после переходного процесса состояние выходного сигнала одно и то же, а во время переходного процесса возможно кратковременное появление противоположного сигнала.

При динамическом риске сбоя до и после переходного процесса состояния выходного сигнала противоположные, но в переходном процессе выходной сигнал несколько раз меняет свое значение. Динамический риск сбоя возможен в схеме (рис.12 а) при смене набора (Х1=0, Х2=1, Х3=1) на набор (Х1=1, Х2=0, Х3=0) и иллюстрируется диаграммами

(рис.12 б).

В данном примере динамический риск сбоя на выходе КС сопровождается статическим на выходе элемента 1. Как видно из временных диаграмм риск сбоя имеет место при наличии определенного временного сдвига между сигналами, поступающими на вход ЛЭ. Нежелательные сигналы на выходе могут и отсутствовать при другом соотношении временных сигналов, однако принципиальная возможность их появления является фактором снижающим надежность работы схемы. Поэтому очень важно уметь обнаруживать и устранять такие явления.

X3

X1	&	e1
X2
	1
X3

1	e2 = Y	X2
2
		X1

Рис. 12 а- схема, б- временные диаграммы.	e1
	Y

Для анализа процесса переключения КС при смене входных наборов и обнаружения рисков сбоя используется метод асинхронного моделирования. При этом методе считается, что каждый элемент переключается с одинаковой задержкой. Анализ включает такие этапы:

Лекция 6

ТЕОРИЯ АБСТРАKТНЫХ АВТОМАТОВ

6.1. Основные понятия и определения

Ознакомившись в курсах "Программирование" и "Машинная арифметика" с принципами работы ЭЦВМ, можно указать на две основные особенности таких вычислительных машин: оперирование данными, представленными в цифровой форме и автоматическая работа по заранее составленной программе. Эти особенности показывают, что любая ЭЦВМ является цифровым автоматом (ЦА). Понятие ЦА служит обобщением для всех видов устройств обработки цифровой информации, имеющих программное управление.

Цифровой автомат - устройство, характеризующееся набором внутренних состояний в которое оно попадет под воздействием команд заложенной в него программы. Переход автомата из одного состояния в другое осуществляется в определенный момент времени.

Математической моделью ЦА (а в общем случае любого дискретного устройства) является так называемый абстрактный автомат, определенный как 6-компонентный кортеж: S=(A,Z,W,δ,λ,а1) у которого:

1.A={a1, a2, ... ,am} - множество состояний (внутренний алфавит)

2.Z={z1, z2, ... ,zf} - множество входных сигналов (входной алфавит)

3.W={w1, w2, ..., wg} - множество выходных сигналов (выходной алфавит)

4.δ : A•Z→A - функция переходов, реализующая отображение Dδ А•Z в А. Иными словами функция δ некоторым парам состояние - входной сигнал (аm, zf) ставит в соответствие состояния автомата аs= δ (am, zf), as A.

5.λ : A•Z→W - функция выходов, реализующая отображение Dλ А•Z на W. Функция λ

некоторым парам состояние - входной сигнал (аm, zf) ставит в соответствие

выходные сигналы автомата Wg=λ(аm, zf) , Wg W.

6. ai A - начальное состояние автомата.

Под алфавитом здесь понимается непустое множество попарно различных символов.

Элементы алфавита называются буквами, а конечная упорядоченная последовательность букв - словом в данном алфавите.

Z	S	W

Рис. 14 Абстрактный автомат.

Абстрактный автомат (рис.14) имеет один вход и один выход. Автомат работает в дискретном времени, принимающем целые неотрицательные значения t = 0,1,2,... В каждый момент t дискретного времени автомат находится в некотором состоянии a(t) из множества состояний автомата, причем в начальный момент t = 0 он всегда находится в начальном состоянии a(0)=a1. В момент t, будучи в состоянии a(t), автомат способен воспринять на входе букву входного алфавита z(t) Z. В соответствии с функцией выходов он выдаст в тот же момент времени t букву выходного алфавита W(t)=λ(a(t), z(t)) и в соответствии с функцией переходов перейдет в следующее состояние a(t+1)=δ[a(t), z(t)], a(t) A, w(t) W.

Смысл понятия абстрактного автомата состоит в том, что он реализует некоторое отображение множества слов входного алфавита Z во множество слов выходного алфавита

W. Т.е. если на вход автомата, установленного в начальное состояние a1, подавать буква за буквой некоторую последовательность букв входного алфавита z(0), z(1),... - входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита w(0), w(1),... - выходное слово. Т.о. выходное слово = ϕ(входное слово), где ϕ - отображение, осуществляемое абстрактным автоматом.

На уровне	абстрактной	теории понятие "работа автомата" понимается как
преобразование входных слов в		выходные. Можно сказать, что в абстрактном автомате

отвлекаемся от его структуры - содержимого прямоугольника (рис. 14 ), рассматривая его как "черный ящик", т.е. основное внимание уделяем поведению автомата относительно внешней среды.

Понятие состояния в определении автомата введено в связи с тем, что часто возникает необходимость в описании поведения систем, выходы которых зависят не только от состояния входов в данный момент времени, но и от некоторой предыстории, т.е. от сигналов, которые поступали на входы системы ранее. Состояния как раз и соответствуют некоторой памяти о прошлом, позволяя устранить время как явную переменную и выразить выходной сигнал как функцию состояния и входа в данный момент времени.

На практике наибольшее распространение получили два класса автоматов - автоматы Мили (Mealy) и Мура (Moore).

Закон функционирования автомата Мили задается уравнениями:

a(t+1) = δ(a(t), z(t)); w(t) = λ(a(t), z(t)), t = 0,1,2,...

Закон функционирования автомата Мура задается уравнениями:

a(t+1)=δ(a(t), z(t)); w(t) = λ(a(t)), t = 0,1,2,...

Из сравнения законов функционирования видно, что, в отличие от автомата Мили, выходной сигнал в автомате Мура зависит только от текущего состояния автомата и в явном виде не зависит от входного сигнала. Для полного задания автомата Мили или Мура дополнительно к законам функционирования, необходимо указать начальное состояние и определить внутренний, входной и выходной алфавиты.

Кроме автоматов Мили и Мура иногда оказывается удобным пользоваться совмещенной моделью автомата, так называемым С- автоматом.

Под абстрактным С- автоматом будем понимать математическую модель дискретного устройства, определяемую восьмикомпонентным вектором S=( A, Z, W, U, δ, λ1, λ2, а1 ), у которого:

1.A={a1, a2, ... ,am} - множество состояний;

2.Z={z1, z2, ... ,zf} - входной алфавит;

3.W={w1, w2, ..., wg} - выходной алфавит типа 1;

4.U={u1, u2,...,uh} - выходной алфавит типа 2;

5.δ : A • Z → A - функция переходов, реализующая отображение Dδ А•Z в А;

6.λ1 : A • Z → W - функция выходов, реализующая отображение Dλ1 А•Z в W;

7.λ2 : A → U - функция выходов, реализующая отображение Dλ2 А в U;

8.а1 А - начальное состояние автомата.

Абстрактный С- автомат можно представить в виде устройства с одним входом, на который поступают сигналы из входного алфавита Z, и двумя выходами, на которых появляются сигналы из алфавитов W и U. Отличие С - автомата от моделей Мили и Мура состоит в том, что он одновременно реализует две функции выходов λ1 и λ2, каждая из которых характерна для этих моделей в отдельности. Закон функционирования С- автомата можно описать следующими уравнениями: