Условия интегрируемости функций

Рассмотрим условия интегрируемости функций на отрезке , т. е. условия существования определенного интеграла. При опреде­лении его как предела интегральной суммы мы предпо­лагали, что функция ограничена на отрезке . Условие огра­ниченности функций на отрезке является необходимым усло­вием интегрируемости функций, т. е. справедлива следующая

Теорема. Если существует, то функция ограничена на отрезке .

Ограниченность является необходимым, но не достаточным условием интегрируемости функции на отрезке , т. е. что существуют ограниченные функции, не являющиеся интегрируемыми.

Сформулируем без доказательства достаточное условие интегри­руемости функции.

Теорема. Если функция непрерывна на отрезке , то она интегрируема на этом отрезке, т. е. существует .

Отметим, что интеграл Римана существует для значительно более широкого класса функций, нежели рассматриваемый класс непре­рывных функций. В частности, справедлива следующая теорема, обобщающая предыдущую теорему

Теорема. Если функция ограничена на отрезке и непрерывна на нем всюду, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке, т. е. существует .

Основные свойства определенного интеграла

Рассмотрим свойства определенного интеграла, доказательство которых основывается на определении определенного интеграла.

1. Если нижний и верхний пределы интегрирования равны ( = ), то интеграл равен нулю:

2. Если = 1, то

3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:

4. Постоянный множитель можно выносить за знак определен­ного интеграла:

.

5. Определенный интеграл от алгебраической суммы конечного числа интегрируемых на функций равен алгебраической сумме определенных интегралов от слагаемых: .

6(Аддитивность определенного интеграла). Если существуют интегралы и , то существует также интеграл и для любых чисел , ,

.

Геометрический смысл свойства 6 состоит в том, что площадь криволинейной трапеции с основанием равна сумме площадей криволинейных трапеций с основаниями и .

7. Если 0 для , то

0, ()

8(Монотонность определенного интеграла). Если интегрируемые функции и удовлетворяют неравенству  для , то

, ()

9 (Об оценке определенного интеграла). Если и — соот­ветственно наименьшее и наибольшее значения функции , не­прерывной на отрезке , то

. (1)

Доказательство. По условию  для , следовательно, по свойству 8

 ,

.

⊠

На рисунке дана геометрическая интерпретация свойства 9 в случае, когда 0 . Площадь прямоугольника равна , площадь прямоугольника равна . Из неравенства (1) следует, что площадь криволинейной трапеции не меньше площади первого прямоугольника и не больше площади второго.

10(Теорема о среднем). Если функция непрерывна на от­резке , то существует такая точка , что

. (2)

т. е. определенный интеграл от непрерывной функции равен произ­ведению значения подынтегральной функции в некоторой промежу­точной точке отрезка интегрирования и длины этого отрезка.

Доказательство. Так как непрерывна на отрезке , то она по теореме Вейерштрасса до­стигает на своего наименьшего и наибольшего значений, т. е.

 для .

Из данного неравенства на основании свой­ства 9 имеем

.

Разделив все члены двойного неравенства на > 0, получим



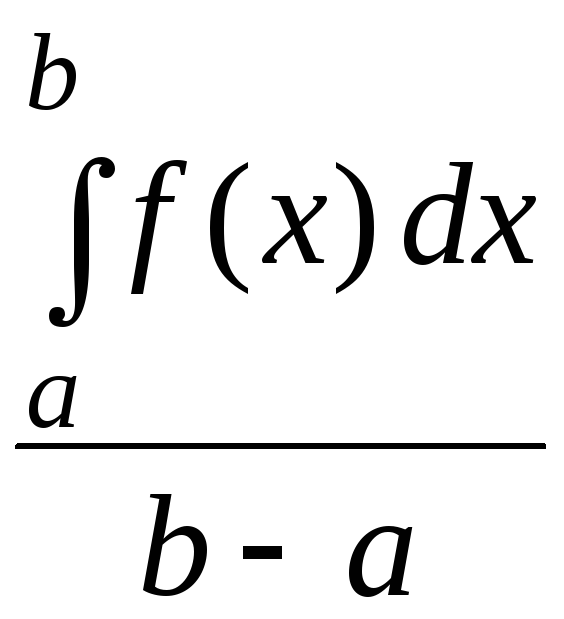
Обозначим , тогда .

Другими словами, число находится между наимень­шим и наибольшим значениями функции . Поскольку непрерывная на отрезке функция по теореме Больцано-Коши принимает все промежуточные значения, лежащие между и , в том числе и значение , то суще­ствует , такое, что = , то есть

, .

⊠

Число при этом называется интеграль­ным средним значением функции на отрезке .

На рисунке дана геометрическая интерпретация свойства 10 в случае, когда > 0 . Так как значение () числен­но равно площади прямоугольника с основанием и высотой , то теорема о среднем утверждает, что существует прямоугольник, равновеликий криволинейной трапеции .