10.2. Еквівалентність множин

Якщо існує бієктивна аплікація множини A на B, множини A і B називаються еквівалентними. Дійсно, можемо назвати ці множини еквівалентними, тому що задовольняють всім умовам еквівалентності:

A ( A (в цьому випадку f = I_A : A ( A) – рефлексивна;

Якщо A ( B, то B ( A (так як f є бієктивна, існує f ^-1: B( A) – симетрична;

c) Якщо A ( B і B ( C, тоді A ( C (в цьому випадку існують f: A ( B і g: B ( C обидві бієктивні, тому g(f: A( C також бієктивна) – транзитивна.

Приклади. 1. Множини точок двох концентричних кіл є еквівалентні – бієктивна аплікація легко встановлюється геометрично провівши радіус більшого кола. Те ж саме можна сказати і про множини точок еліпса і кола.

Рис. 1

2. Множина точок катета є еквівалентна множині точок гіпотенузи

Фіг. 2

3. Множина парних чисел є еквівалентне множині всіх натуральних чисел.

1 2 3 4 5 6 … n …

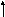
2 4 6 8 10 12 … 2n …

В останньому випадку можемо вжити аплікацію y = 2x N в N, яка є бієктивна.

4. Інтервал (0, 1) є еквівалентним всій числовій осі (-(,( ). Щоб впевнитися в цьому дослідимо функцію

.

Зверніть увагу, що в наведених вище прикладах одна з множин є власною підмножиною іншої, їй еквівалентної. Це може бути лише для нескінчених множин. На протязі тисячоліть математики думали, що нескінчені множини мають ті ж самі властивості, що і скінчені і не сприймали того факту, що множина може бути еквівалентна своїй частині. Ціле завжди вважалось більшим за його частину. Але робота з нескінченими множинами потребує нового, більш глибокого розуміння поняття множини, і перший, хто звернув на це увагу був Georg Cantor, який поклав вказану особливість нескінчених множин в основу їх визначення ele colocou o na definicao do conjunto infinito.

Множина еквівалентна своїй власній підмножині є нескінченою

10.3. Класи еквівалентності

Розглянемо множину E в якій визначено відношення еквівалентності і C_R(a) позначимо множину елементів еквівалентних a. Назвемо цю множину класом еквівалентності.

Teorema 1. Всі елементи класу C_R(a) еквівалентні між собою.

Prova. Нехай x ( y, x( C_R(a) і y ( C_R(a) . Тоді, x ( a, y ( a. Із рефлективності еквівалентності a ( y, із транзитивності x ( y, що й треба було довести.

Teorema 2. Два класи еквівалентності, що мають спільний елемент є ідентичними.

Prova. Нехай x( C_R(a) ( C_R(b). Тоді, x( C_R(a) і згідно теореми 1 x є еквівалентним всім елементам класу C_R(a). Їз рефлективності слідує, що всі елементи C_R(a) еквівалентні x, які в свою чергу еквівалентні b, тому належать C_R(b) . Значить, всі елементи C_R(a) належать C_R(b), отже C_R(a) ( C_R(b). Таким же способом доведемо, що C_R(b) ( C_R(a). Звідси слідує

C_R(a) = C_R(b).

10.4. Розбиття множини

Розбиттям множини E називається множина F підмножин E таких, що

.

Приклади. A = {a, b, c}. Можливі розбиття:

A₁ = {a}, A₂ = {b}, A₃ = {c};

A₁ = {a, b}, A₂ = {c};

A₁ = {a, c}, A₂ = {b}, etc.

Теорема 3. Відношення еквівалентності E робить розбиття цієї множини.

Доведення. Розглянемо відношення еквівалентності на множині E. Кожен елемент E належить одному з класів еквівалентності. Згідно теореми 2 ці класи не мають спільних елементів. Згідно ж означення 2 вони утворюють розбиття множини E.