§4. Закон інерції квадратичних форм

При зведенні квадратичної форми А(x, x) до суми квадратів різними способами можна отримати різні канонічні коефіцієнти . Однак має місце наступне твердження :

Теорема (закон інерції квадратичних форм).

Кількість доданків з додатніми (від’ємними) канонічними коефіцієнтами в канонічному вигляді квадратичної форми не залежить від способу зведення форми до цього вигляду.

Доведення (від супротивного).

Припустимо , що в базисі e=(e₁, e₂,…, e_n) квадратична форма А(x, x) має вигляд

А(x, x) , (*)

де – координати вектора x в цьому базисі, і нехай в іншому базисі e₁^’, e₂^’,…, e_n^’

А(x, x) , (**)

де – координати вектора x в новому базисі. Припустимо, що, наприклад, p>k.

Розглянемо в просторі V підпростір , породжений векторамиe₁, e₂,…, e_n, і підпростір , породжений векторами. Оскільки сума їх розмірностейp+(n-k) більша за n, то їх перетин має ненульову розмірність, тобто існує вектор , який належить. Цей вектор можна подати як у вигляді

,

так і у вигляді

.

Для вектора х за формулою (*)

А(x, x) ,

оскільки хоча б одне із .

В той же час для вектора х за формулою (**)

А(x, x) .

Ми отримали протиріччя, із якого випливає, що pk. Аналогічно доводиться: неможливість нерівності p<k. Значить, p=k. Так само доводиться, що q=m.

Ясно, що сума p+ q дорівнює рангу r квадратичної форми.

Приклад. Дослідити знаковизначеність квадратичної форми

.

Розв’язання. Запишемо матрицю цієї форми

.

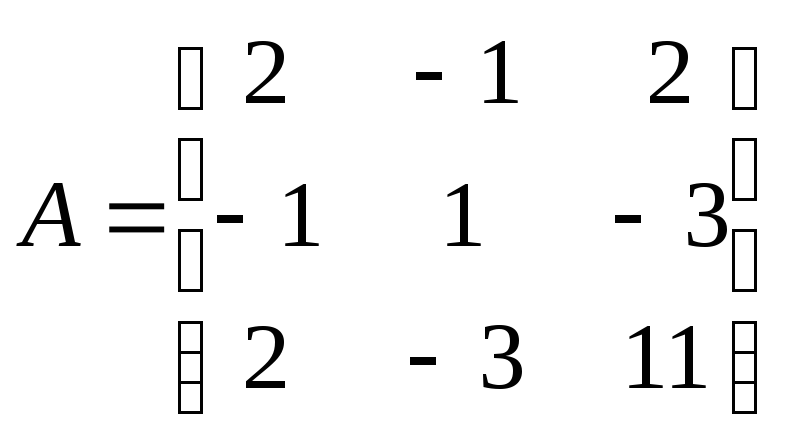Обчислимо кутові мінори:

,

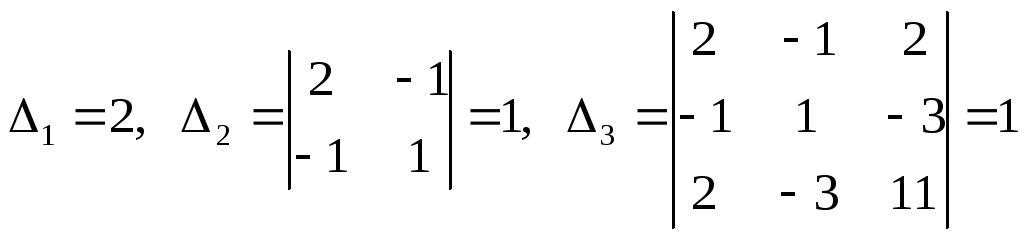отже, задана квадратична форма додатньовизначена.

§5. Класифікація квадратичних форм

Квадратична форма називається додатньо (від’ємно) визначеною, якщо для А(x, x) (А(x, x)) і додатньо (від’ємно) напіввизначеною (квазівизначеною), якщо А(x, x) (А(x, x) ).

Приклад.

Скалярний квадрат А(x, x) = (х,х) є додатньо визначеною квадратичною формою.

Ясно, що додатньо визначена квадратична форма зводиться до суми квадратів з додатніми канонічними коефіцієнтами, додатньо напіввизначена форма – з невід’ємними коефіцієнтами (деякі з них можуть дорівнювати нулю).

Теорема (критерій Сильвестра).

Для того, щоб квадратична форма А(x, x) була додатньо визначеною, необхідно і достатньо, щоб всі кутові мінори матриці А=[a_ij] були додатніми.

Для того ж, щоб квадратична форма була від’ємно визначеною, необхідно і достатньо, щоб знаки кутових мінорів чергувались, причому .

Доведення..

а)Необхідність. Покажемо спочатку, що із умови знаковизначеності квадратичної форми А(x, x) випливає ,і=1, 2,..., n.

Переконаємось, що припущення веде до протиріччя – при цьому припущенні існує ненульовий векторх, для якого А(x, x), що суперечить знаковизноченості форми.

Нехай . Розглянемо наступну квадратну однорідну систему лінійних рівнянь:

.

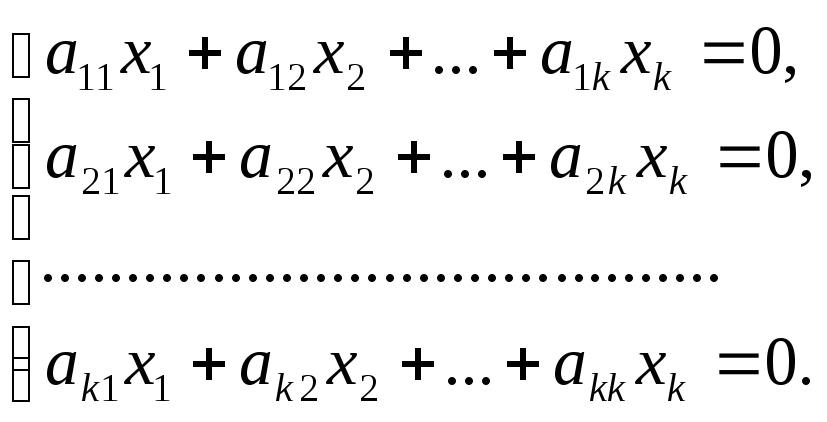Оскільки - визначник цієї системи, і=0, то записана система рівнянь має ненульові розв’язки (не всі х рівні нулю ). Помножимо перше із рівнянь системи на , друге на, ..., останнє наі додамо отримані співвідношення. В результаті дістанемо рівність, ліва частина якої є значенням квадратичної формиА(x, x) для ненульового вектора х з координатами . Це значення рівне нулю, що суперечить знаковизначеності форми. Отже,,і=1,2,...,n.

Застосуємо метод Якобі зведення форми А(x, x) до суми квадратів. Якщо А(x, x) –додатньо визначена форма, то із формул для знаходження канонічних коефіцієнтів отримаємо ...,. Якщо ж А(x, x)– від’ємно визначена форма, то з тих же формул випливає, що знаки кутових мінорів чергуються, причому.

б) Достатність. Згідно умови теореми всі ,і=1,2,...,n, тому, скориставшись методом Якобі, отримаємо у першому випадку додатньо, а в другому – від’ємно визначену квадратичну форму.