5.2. Статистическая обработка результатов испытаний и их критерии

5.2.1. Статистическая обработка результатов испытаний

Для решений теоретических и практических задач надёжности необходимо знать законы распределения случайных величин. Обработка статистического материала позволяет определить законы распределения отказов.

При эксплуатации или испытании изделия случайная величина Тв течение некоторого интервала времениtможет принятьпразличных значений. Совокупность этих значений случайной величины называетсястатистической выборкой объёмомп.

При большом числе пудобнее от статистической выборки перейти кстатистическому ряду. Для этого весь диапазон значений случайной величиныТразбивается на интервалы. Подсчитав количество значенийт_iслучайной величиныТ, приходящихся на каждыйi–й интервал, определяют частоту (частость) её попадания в данный интервал:

p_i^*=m_i/n. (5.6)

В этом случае статистический ряд представляется в виде табл. 5.2.

Таблица 5.2

Статистический ряд

Интервалы	t1 – t2	t2 – t3	…	ti – ti+1	…	tk – tk+1
Частота	p1^*	p2^*	…	pi^*	…	pk^*

Величина интервала определяется как

, (5.7)

где Т_maxиT_min– максимальное и минимальное значенияТв сводке величин.

Для удобства рассчитанный интервал Δt′округляется до целых десятков или сотен. Тогда число интервалов равно

. (5.8)

При разбивке случайной величины число интервалов не должно быть слишком большим, чтобы в частотах p_i^*не обнаружились её незакономерные колебания. При малом же числе интервалов статистический ряд грубо описывает характер распределения. Поэтому целесообразно выбирать число интервалов порядка 10 – 20. Однако при большом статистическом материале это число может быть увеличено.

Наглядное представление о законах распределения случайной величины дают статистические графики, например такой, как гистограмма.

Гистограмма строится следующим образом. На каждом отрезке оси абсцисс, изображающим интервал, строится прямоугольник, площадь которого пропорциональна частоте появления случайной величины в этом интервале. Если интервалы имеют одинаковую ширину, что обычно и бывает, то высоты прямоугольников пропорциональны частотам.

При увеличении числа опытов пдля каждого интервала можно выбирать всё мéньшую продолжительность. В этом случае гистограмма будет приближаться к некоторой плавной кривой. Следовательно, такая кривая соответствует графику функции плотности распределения некоторой случайной величиныТ.

5.2.2. Критерии согласия и доверительные интервалы

Под «выравниванием» статистического ряда подразумевается такая обработка статистических данных, при которой обеспечивается подбор наиболее подходящего теоретического закона распределения. При этом закон распределения может быть описан либо функцией распределения F(t), либо плотностью распределенияf(t).

Для оценки степени расхождения полученного статистического распределения F^*(t) с теоретическим законом распределенияF(t) выбирается такая мера расхождения, по величине которой можно было бы судить о том, вызвано ли это расхождение случайными причинами, либо разница между распределениями такова, что выбранный теоретический законF(t) непригоден.

При «выравнивании» статистического ряда обычно стремятся выбрать такую аппроксимирующую функцию φ₀(t), которая, в то же время, действительно согласовывалась бы с данными эксперимента, т. е. чтобы можно было считать справедливым равенство

φ₀(t) ≈F(t). (5.9)

Для оценки правдоподобия этого приближённого вероятностного равенства разработаны несколько критериев согласияпроверяемых гипотез относительно вида функций φ₀(t) иF(t).

Идея применения критериев согласия заключается в следующем. Предпо-лагается, что случайная величина Т, полученная в виде статистического ряда, подчинена некоторому определённому закону распределения, описываемому функцией распределенияF(t).

Для проверки справедливости такой гипотезы вводится вспомогательная величина Δ, которая может быть выбрана различными способами, но так чтобы она могла служить мерой расхождения между теоретическим и статистическим законами распределения.

Поскольку для разных опытов статистические данные носят случайный характер и функция F^*(t) для каждого опыта будет иметь другой вид, то мера расхождения Δ является случайной величиной.

Если гипотеза о том, что величина Тподчиняется закону распределенияF(t) справедлива, то закон распределения Δ будет определяться законом распределенияТи числом опытов.

Это обстоятельство и позволяет установить согласие между теоретическим и статистическим распределениями, если известен закон распределения Δ.

Предположим, что закон распределения выбранной меры расхождения Δ известен.

В результате эксперимента установлено, что выбранная мера расхождения приняла некоторое конкретное значение u.

Для того чтобы выяснить, является ли это расхождение случайным за счёт ограниченности числа опытов, или оно свидетельствует о наличии существенной разницы между теоретическим и статистическим распределениями, необходимо вычислить вероятность получения такого расхождения при принятом законе F(t) и заданномп.

При известной функции Δ это вычисление сводится к определению события, что Δ ≥ u, т. е.р{Δ ≥u}.

Если эта вероятность окажется малой, то теоретическое распределение выбрано неудачно. В этом случае гипотеза о том, что F(t) «выравнивает» статистическое распределениеF^*(t), малоправдоподобна.

Если же вероятность значительна, то можно считать, что эксперименталь-ные данные не противоречат сделанному допущению о подчинении случайной величины Тзакону распределенияF(t).

Оказывается, что при некоторых способах выбора меры расхождения ∆ закон распределения этой величины может быть определён заранее теоретически, исходя из общих положений теории вероятностей, и при достаточно большом пне зависит от вида функцииF(t), что значительно облегчает применение критериев согласия.

Наиболее употребительными критериями согласия являются критерии Пирсона и А.Н. Колмогорова.

А. Критерий Пирсона.В качестве меры расхождении ∆ для этого критерия выбрана величина, определяемая уравнением

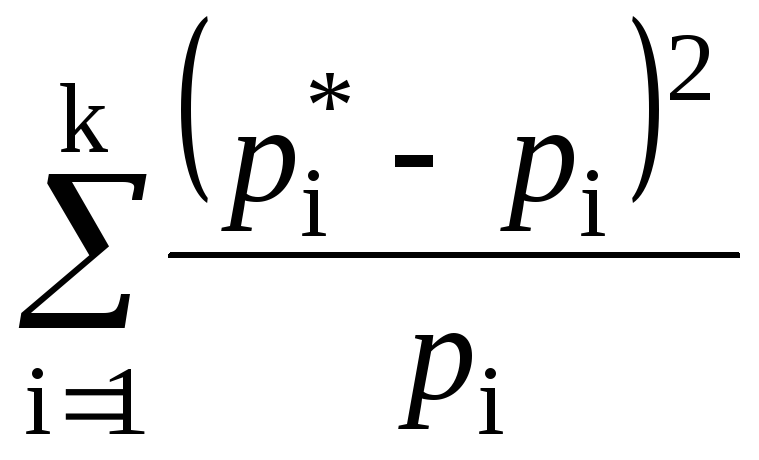∆ = , (5.10)

где п– общее число опытов;k– число интервалов статистического ряда;p_i^*=m_i/n– частотаi–го интервала статистического ряда;p_i– теоретическая вероятность попадания случайной величины вi–й интервал.

Оказывается, что при таком выборе меры расхождения ∆ закон распределения её величины при увеличении k(k→ ∞) приближается к известному в теории вероятностей распределению χ²(хи–квадрат), а следовательно, не зависит от вида теоретической функции распределения и числа опытов, а определяется только числом разрядов (интерваловk) статистического ряда.

В силу сказанного при использовании критерия Пирсона мера расхожде-ния ∆ обычно обозначается как χ².

Учитывая соотношение p_i=m_i/n, уравнение для χ²записывается в следующем виде:

χ²=, (5.11)

где m_i,nиk– известные по данным опыта, а теоретическая вероятностьp_iвычисляется, исходя из принятого для «выравнивания» статистического ряда теоретического закона распределенияF(t), как вероятность попадания случайной величины в каждый из разрядов:

. (5.12)

Следовательно, для любого i–го интервала оказывается известным некоторое определённое значение.

Поскольку величина ∆ известна и определяется в соответствии с уравнением (5.10), то оценка степени расхождения определяется как вероятность события ∆ ≥ , т. е. сводится к определению вероятности попадания случайной величины ∆ на участок отдо + ∞:

. (5.13)

Интеграл, стоящий в правой части табулирован, а поэтому при известных значениях r, (r=k– 1 – число степеней свободы распределения) имогут быть определены по таблицам величина вероятности.

Если эта вероятность очень мала (практически меньше 0,1), то выбранное теоретическое распределение следует считать неудачным. При относительно большом значении вероятности выбранное теоретическое распределение можно признать не противоречащим опытным данным.

Критерий Пирсона применим в тех случаях, когда количество опытов достаточно велико (порядка сотен), а в каждом разряде число наблюдений m_iне менее пяти.

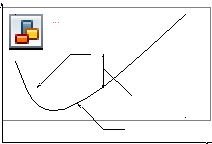
Б. Критерий А.Н. Колмогорова.Сущность критерия сводится к следующему. На график (см. рис. 5.1) наносят значения степенной функции распределения, соответствующей статистическим даннымF^*(x), и выбранной аппроксимирующей функцииF(x).

F^*(x), F(x)

F^*(x)

D

F(x)

x

Рис. 5.1

В качестве меры расхождения между ними выбирается величина , удовлетворяющая неравенству

, (5.14)

где п– объём статистической выборки;D– максимальное отклонение статистической функции распределенияF^*(x) от теоретическойF(x):

D = max |F(x) – F^*(x)|. (5.15)

Эта величина может быть найдена непосредственно из графика.

А.Н. Колмогоровым была доказана теорема, согласно которой для любой непрерывной функции при неограниченном возрастании числа опытов вероятность неравенства стремится к пределу, определяемому рядом

, (5.16)

т. е.

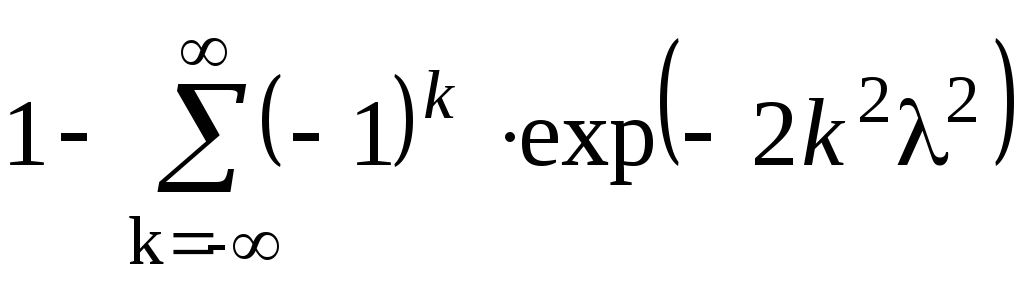limp{} =lim[] =p(λ), (5.17)

где p(λ) – табулированная функция (см. табл. 5.3).

Таблица 5.3