
ВЫЧ.МАТ. Лекции и задания / ИНТЕРПОЛЯЦИЯ пособие
.rtfИНТЕРПОЛЯЦИЯ
Пусть
дана функция
 и фиксированная величина приращения
аргумента
и фиксированная величина приращения
аргумента
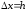 .
Конечной разностью первого порядка
функции y
называется выражение.
.
Конечной разностью первого порядка
функции y
называется выражение.
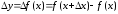 Конечной разностью второго порядка
называется:
Конечной разностью второго порядка
называется:
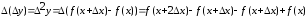 .
Kонечной
разностью n-го
порядка называется
.
Kонечной
разностью n-го
порядка называется
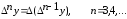 .
Конечные разности обладают следующими
свойствами :
.
Конечные разности обладают следующими
свойствами :
-
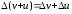 ;
; -
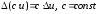 ;
; -
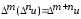 .
.
Для
малых h
можно
приближенно заменять производные через
конечные разности:
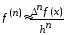 ,
(
,
(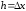 ).
).
Таблица разностей.
Часто приходится рассматривать функции у=f(x,), заданные табличными значениями yi=f(xi,) для системы равноотстоящих точек xi (i=0,1,2,…), где
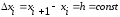 конечные
разности последовательности yi
определяются
соотношениями
конечные
разности последовательности yi
определяются
соотношениями
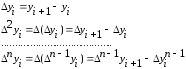
Пример.
Построить конечные разности для функции
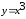 с шагом
с шагом
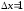 .
.
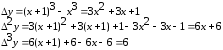
Конечные разности различных порядков удобно располагать в форме таблиц двух видов: горизонтальной (таблица 3.1) или диагональной (таблица 3.2)
Горизонтальная таблица разностей Таблица 3.1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
…. |
… |
… |
… |
… |
… |
Диагональная таблица конечных разностей:
Диагональная таблица конечных разностей Таблица 3.2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
||||
|
|
|
|
||
|
|
||||
|
|
|
Постановка задачи интерполирования
Пусть
функция
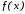 задана на отрезке
задана на отрезке
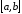 в точках
в точках
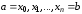 ,
,
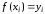 i=0,1,2..n
i=0,1,2..n
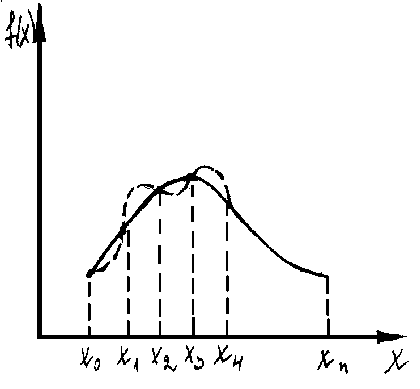 где
где
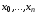 - узлы интерполяции.
- узлы интерполяции.
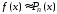
Нам
нужно провести интерполирующую функцию
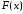 определенного класса, проходящую через
точки:
определенного класса, проходящую через
точки:
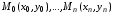 ,
т.е. в узлах интерполяции
,
т.е. в узлах интерполяции i=1,2..n.
Пусть
i=1,2..n.
Пусть
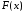 - это многочлен степени не выше n.
В такой постановке задача имеет
единственное решение. Полученную формулу
- это многочлен степени не выше n.
В такой постановке задача имеет
единственное решение. Полученную формулу
y=F(x)
используют для вычисления приближенного значения функции f(x) для значений аргумента x, отличных от узлов интерполяции. Эта операция называется интерполирование.
Интерполирование
в узком смысле, если
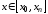 ,и
экстраполирование (интерполирование
в широком смысле). если
,и
экстраполирование (интерполирование
в широком смысле). если
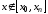
Интерполяционная формула Ньютона №1
Пусть
точки будут равноотстоящими. Дано:
отрезок
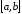 ,
,
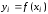 ,
,
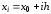 .
.
Тогда:
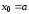 ,
,
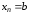 ,
,
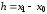 -
шаг интерполяции.
-
шаг интерполяции.
Требуется:
подобрать полином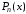 ,
степени не выше n
, принимающий в точках значения
,
степени не выше n
, принимающий в точках значения
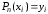 или
или
 .
.
Идея
Ньютона находить решение в виде полинома
 :
:
где
 .
.
Для
практического использования удобно
положить
 ,
тогда
,
тогда
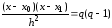 .
…
.
…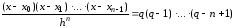
Получим:
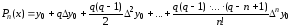
- первый многочлен Ньютона.
Полученную
формулу выгодно использовать для
интерполирования функции
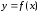 в окрестности начального значения x0,
где q
мало по абсолютной величине.
в окрестности начального значения x0,
где q
мало по абсолютной величине.
При n=1 получим формулу линейного интерполирования
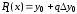
Остаточный
член
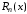 первой интерполирующей формулы Ньютона
имеет вид:+
первой интерполирующей формулы Ньютона
имеет вид:+
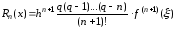 ,
,
где
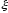 - некоторая внутренняя точка наименьшего
промежутка, содержащего все узлы
- некоторая внутренняя точка наименьшего
промежутка, содержащего все узлы
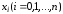 и
точку
и
точку
 .
.
При
наличии дополнительного узла
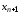 на практике пользуются более удобной
приближенной формулой:
на практике пользуются более удобной
приближенной формулой:
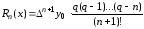 .
.
Интерполяционная формула Ньютона №2
Первая интерполяционная формула Ньютона практически неудобна для интерполирования вблизи конца таблицы. В этом случае обычно применяется вторая интерполяционная формула Ньютона.
Пусть
имеем систему значений функции
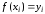 для равноотстоящих значений аргумента
для равноотстоящих значений аргумента
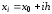 ,
где
,
где
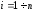 .
Построим интерполирующий полином
следующего вида.
.
Построим интерполирующий полином
следующего вида.
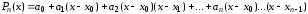 ,где
,где
 .
Подставляя эти значения в формулу и,
полагая
.
Подставляя эти значения в формулу и,
полагая

получим:
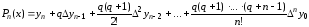
.
- второй многочлен Ньютона.
Остаточный
член
 второй интерполирующей формулы Ньютона
имеет вид:
второй интерполирующей формулы Ньютона
имеет вид:
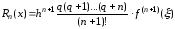 ,
,
где
 - некоторая внутренняя точка наименьшего
промежутка, содержащего все узлы
- некоторая внутренняя точка наименьшего
промежутка, содержащего все узлы
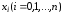 и
точку
и
точку
 .
.
Для
неограниченной таблицы значений функции
y
число n
в
интерполяционной
формуле может быть любым, поэтому
практически его выбирают так, что бы
разность
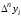 была
постоянной с заданной степенью точности.
была
постоянной с заданной степенью точности.
Если таблица значений функции конечна, то число n не может быть больше числа значений функции у минус единица
Пример.
Найти приближенное значение функции при данном значении аргумента с помощью первого или второго интерполяционного многочлена Ньютона . Вычислить остаточный член.
.
|
|
|
|
x |
y |
|
|
|
|
1.215 |
0.106044 |
|
1.220 |
0.106491 |
|
1.225 |
0.106935 |
|
1.230 |
0.107377 |
|
1.235 |
0.107818 |
|
1.240 |
0.108257 |
|
1.245 |
0.108696 |
|
1.250 |
0.109134 |
|
1.255 |
0.109571 |
|
1.260 |
0.110008 |
|
|
|
Требуется определить значения функции y(x) при следующих значениях аргумента
x1 = 1.2173; x2 = 1.253; x3 = 1.210; x4 = 1.270.
Составим таблицу конечных разностей.
|
i |
xi |
yi |
yi |
2yi |
3yi |
|
|
|
|
|
|
|
|
1 |
1.215 |
0.106044 |
0.000447 |
-0.000003 |
0,000001 |
|
2 |
1.220 |
0.106491 |
0.000444 |
-0.000002 |
0,000001 |
|
3 |
1.225 |
0.106935 |
0.000442 |
-0.000001 |
-0,000001 |
|
4 |
1.230 |
0.107377 |
0.000441 |
-0.000002 |
0,000002 |
|
5 |
1.235 |
0.107818 |
0.000439 |
0 |
-0,000001 |
|
6 |
1.240 |
0.108257 |
0.000439 |
-0.000001 |
0 |
|
7 |
1.245 |
0.108696 |
0.000438 |
-0.000001 |
0,000001 |
|
8 |
1.250 |
0.109134 |
0.000437 |
0 |
|
|
9 |
1.255 |
0.109571 |
0.000437 |
- |
|
|
10 |
1.260 |
0.110008 |
- |
- |
|
|
|
|
|
|
|
|
При вычислении разностей ограничиваемся разностями второго порядка, так как они практически постоянны. При х = 1.2173 и х = 1.210 пользуемся формулой Ньютона для интерполирования вперед:
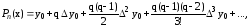
где q = (x-x0)/h.
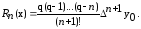
Если
x
= 1.2173, то
 q
= (1.2173-1.215)/0.005= 0.46;
q
= (1.2173-1.215)/0.005= 0.46;
P1(1.2173)=0.106044+0.46·0.000447=0.106044+0.0002056=0.106250

Если x = 1.210, то q = (1.210-1.215)/0.005= -1;
P1(1.210)= 0.106044+(-1)·0.000447=0.105597
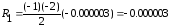
P2(1.210)= P1(1.210)+ R1=0.105600
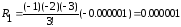
При x = 1.253 и x = 1.270 пользуемся второй формулой Ньютона для интерполирования назад:
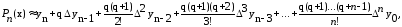
где q = (x-xn)/h.

Если x = 1.253, то q = (1.253 - 1.250)/0.005 = 0.6;
P1(1.253)=0.109134+0.6·0.000438=0.109134+0.000263=0.1093968

Если x = 1.270, то q = (1.270 - 1.260)/0.005 = 2;
P1(1.270)=0.110008+2·0.000437=0.110008+0.000874=0.110882
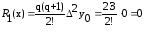
Ответ: f (1.2173) 0.106250; f (1.253) · 0.109397; f (1.210) 0.105597;
f (1.270) 0.110882.
Интерполяционный многочлен Лагранжа
Для произвольно заданных узлов интерполирования пользуются более общей формулой, так называемой интерполяционной формулой Лагранжа.
Пусть
на отрезке
 даны n+1
различных значений аргумента:
даны n+1
различных значений аргумента:
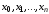 ,
и известны для функции
,
и известны для функции
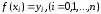 .
Нам нужно построить многочлен
.
Нам нужно построить многочлен
 .
.
Решим
сначала частную задачу, построив полином
такой, что
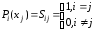 .
.
Т.к.
искомый полином обращается в нуль в n
точках
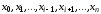 ,
то он имеет вид:
,
то он имеет вид:
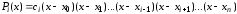 ,
()
,
()
где
 - постоянный коэффициент. Полагая
- постоянный коэффициент. Полагая
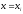 в формуле и учитывая, что
в формуле и учитывая, что
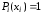 ,
получим:
,
получим:
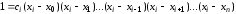 .
.
Отсюда
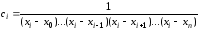 .
.
Вернемся к выражению ():
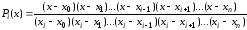 .
.
Тогда
полином Лагранжа имеет следующий вид: 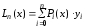 .
.
Докажем единственность полинома Лагранжа.
Предположим
противное. Пусть
 - полином, отличный от
- полином, отличный от
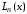 ,
степени не выше n
и такой, что
,
степени не выше n
и такой, что
 .
Тогда полином
.
Тогда полином
 ,
степень которого, очевидно, не выше n,
обращается в нуль в n+1
точках
,
степень которого, очевидно, не выше n,
обращается в нуль в n+1
точках
 ,
т.е.
,
т.е.
 .
Следовательно,
.
Следовательно,
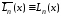 .
.
При
равноотстоящих
 многочлен Лагранжа совпадает с многочленом
Ньютона такой же степени.
многочлен Лагранжа совпадает с многочленом
Ньютона такой же степени.
Вычисление лагранжевых коэффициентов:
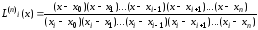 - (1) Можно записать лагранжевы
коэффициенты и более компактно:
- (1) Можно записать лагранжевы
коэффициенты и более компактно: 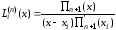 ,
(2)
,
(2)
где
 .
.
Формула
Лагранжа при этом имеет вид
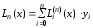 .
.
Для вычисления лагранжевых коэффициентов может быть использована приведенная ниже схема. Сначала располагаем в таблицу разности следующим образом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Обозначим
произведение элементов первой строки
через D0,
второй – D1
и т.д. Произведение же элементов главной
диагонали, очевидно, будет
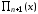 .
Отсюда следует, что
.
Отсюда следует, что
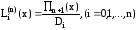 .Следовательно,
.Следовательно,
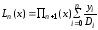 .
.
Пример выполнения в Маткаде
Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лангранжа, если функция задана в неравно- отстоящих узлах таблицы.

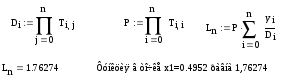
Отметим,
что форма лагранжевых коэффициентов
инвариантна относительно целой линейной
подстановки
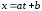 (a,b
– постоянны ). Действительно, положив
в формуле (1):
(a,b
– постоянны ). Действительно, положив
в формуле (1):
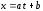 ,
,  ,
,
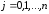 ,
,
после сокращения числителя и знаменателя на a, получим:
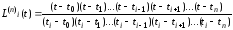
или
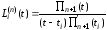 ,
,
где
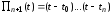 ,
что и требовалось доказать.
,
что и требовалось доказать.
В случае равноотстоящих точек лагранжевы коэффициенты могут быть приведены к более простому виду.
В
самом деле, полагая 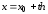 ,
будем иметь:
,
будем иметь:
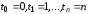 .
Отсюда
.
Отсюда
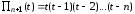 и
и
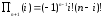 .
.
Тогда
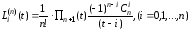 ,
,
где
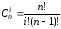 .
Отсюда можно записать:
.
Отсюда можно записать:
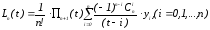 (2)
(2)
где

. Пример выполнения в Маткаде
Найти приближенное значение функции при данном значении аргумента с помощью интерполяционного многочлена Лангранжа, если функция задана в равноотстоящих узлах таблицы


Остаточный член формулы Лагранжа
Остаточный
член равен:
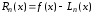 .
Для него справедлива следующая оценка:
.
Для него справедлива следующая оценка:
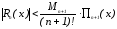 ,
,
где
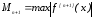 на отрезке
на отрезке
 .
.
Схема Эйткина
Если
требуется найти не общее выражение
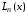 ,
а лишь его значения при конкретных x
и при этом, значения функции даны в
достаточно большом количестве узлов,
то удобно пользоваться интерполяционной
схемой Эйткина. Согласно этой схеме
последовательно вычисляются многочлены:
,
а лишь его значения при конкретных x
и при этом, значения функции даны в
достаточно большом количестве узлов,
то удобно пользоваться интерполяционной
схемой Эйткина. Согласно этой схеме
последовательно вычисляются многочлены:
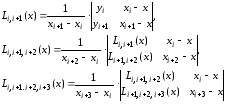 .
.
Интерполяционный
многочлен степени «n»,
принимающий в точках xi
значения
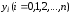 ,
запишется следующим образом:
,
запишется следующим образом:
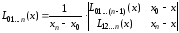 .
.
Вычисления по схеме Эйткена удобно расположить в такой таблице:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
