
- •Практикум з вищої математики. Визначений інтеграл та його застосування
- •1. Визначений інтеграл та його властивості
- •1.1. Означення визначеного інтеграла
- •1.2. Основні властивості визначеного інтеграла Властивості, що виражаються рівностями
- •Властивості, що виражаються нерівностями
- •2. Інтеграл зі змінною верхньою межею. Формула ньютона-лейбниця
- •3. Методи обчислення визначених інтегралів
- •3.1. Метод заміни змінної (підстановки)
- •3.1.1. Підстановка
- •3.1.2. Підстановка
- •2) ; 3).
- •3.1.3. Інтегрування по симетричному проміжку
- •4.1.2. Параметричне задання кривої
- •4.1.3 Задання кривої в полярній системі координат
- •4.2.Обчислення довжин дуг кривих
- •4.2.1.Декартова система координат
- •4.2.2. Параметричне задання кривої
- •4.2.3. Задання кривої в полярній системі координат
- •4.3. Обчислення об’ємів тіл обертання
- •4.3.1 Декартова система координат
- •4.4. Обчислення площ поверхонь тіл обертання
- •1. Якщо криву задано рівняннями в параметричній формі:
- •5. Застосування визначеного інтеграла до розв’язання прикладних задач
- •5.1. Загальна схема застосування визначеного інтеграла
- •5.2. Задача про пройдений шлях
- •5.3. Задача про масу неоднорідного стержня і координати центра мас
- •5.4. Задача про роботу змінні сили
- •6. Завдання для самостійної роботи
- •Варіант 1
- •Практикум з вищої математики.
1.2. Основні властивості визначеного інтеграла Властивості, що виражаються рівностями
1. Сталий множник можна виносити за знак визначеного інтеграла:
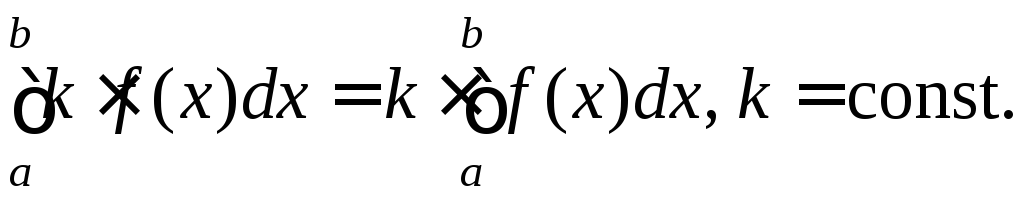
2. Визначений інтеграл від алгебраїчної суми інтегровних функцій дорівнює алгебраїчній сумі інтегралів від ціх функцій:
 .
.
Ця властивість має місце для будь-якого скінченого числа доданків.
3. Аддитивність визначеного інтеграла.
Нехай
функція y = f(x)
є інтегровною на найбільшому з відрізків
![]() Тоді
вона є інтегровною на двох інших
відрізках, і має місце рівність:
Тоді
вона є інтегровною на двох інших
відрізках, і має місце рівність:
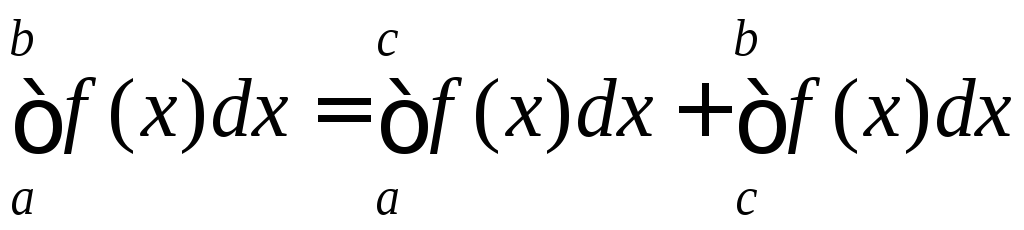
при будь-якому взаємному розташуванні точок a,b, і c.
4. Теорема про середнє значення для визначеного інтеграла.
Нехай
функція f(x)
є неперервною на відрізку
![]() .
Тоді на інтервалі (a,b)
існує
точка с (acb)
така,
що
.
Тоді на інтервалі (a,b)
існує
точка с (acb)
така,
що
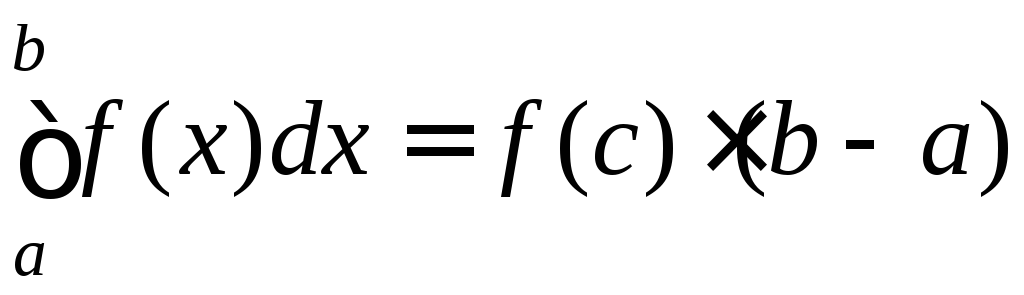 або
або

Значення
![]() називається середнім значенням функції
називається середнім значенням функції![]() на відрізку
на відрізку![]() .
.
Властивості, що виражаються нерівностями
1. Теорема про інтегрування нерівностей.
Нехай
функції
![]() і
і![]() є інтегровними на відрізку
є інтегровними на відрізку![]() і
і![]() .
.
Тоді
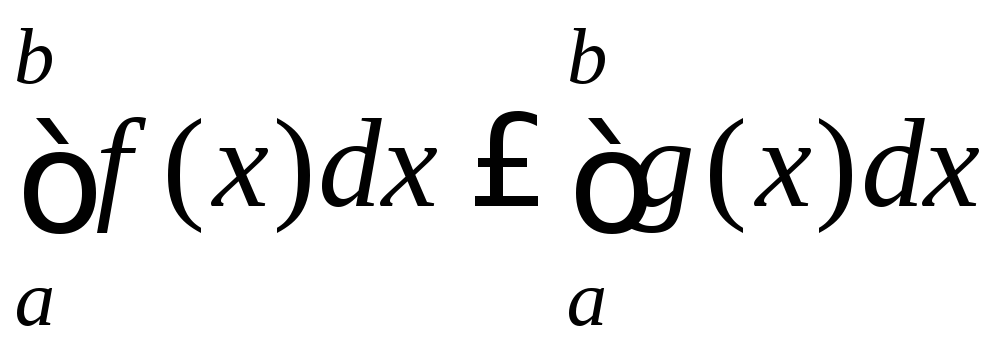 .
.
2. Нехай
функція
![]() є інтегровною на відрізку
є інтегровною на відрізку![]() .
Тоді функція
.
Тоді функція![]() також є інтегровною на цьому відрізку
і має місце нерівність:
також є інтегровною на цьому відрізку
і має місце нерівність:
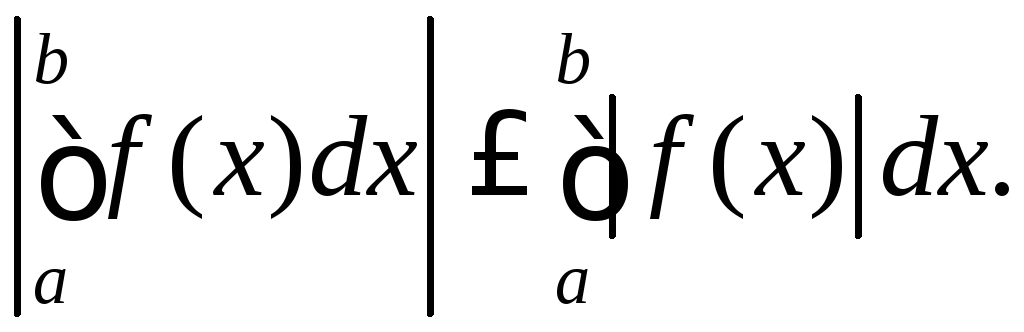
3. Теорема про оцінку визначеного інтеграла.
Нехай
функція
![]() є інтегровною на відрізку
є інтегровною на відрізку![]() і в кожній точці цього відрізка виконується
нерівність
і в кожній точці цього відрізка виконується
нерівність
![]() .
.
Тоді
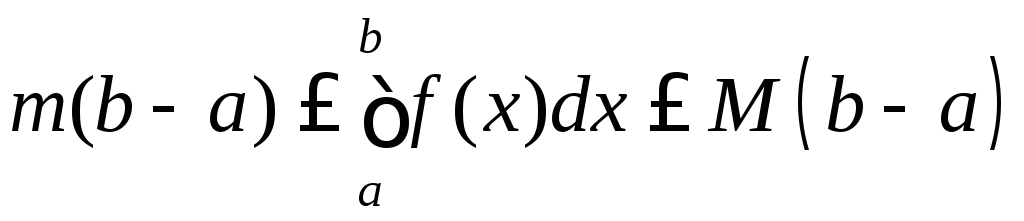 .
.
2. Інтеграл зі змінною верхньою межею. Формула ньютона-лейбниця
Нехай
функція
![]() є неперервною на відрізку
є неперервною на відрізку![]() .
Тоді вона є інтегровною на будь-якому
відрізку
.
Тоді вона є інтегровною на будь-якому
відрізку![]() .
Отже, для довільного
.
Отже, для довільного![]() існує інтеграл
існує інтеграл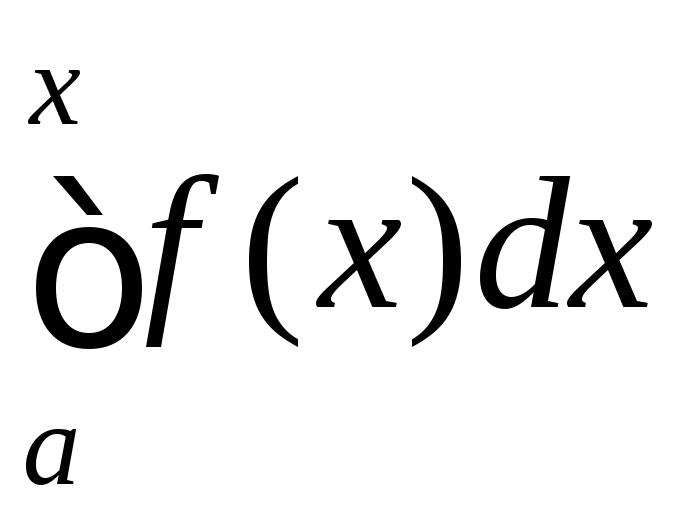 із сталою нижньою межею інтегруванняа
і змінного верхньою межею інтегрування
х.
Цей інтеграл є функцією верхньої межі:
із сталою нижньою межею інтегруванняа
і змінного верхньою межею інтегрування
х.
Цей інтеграл є функцією верхньої межі:
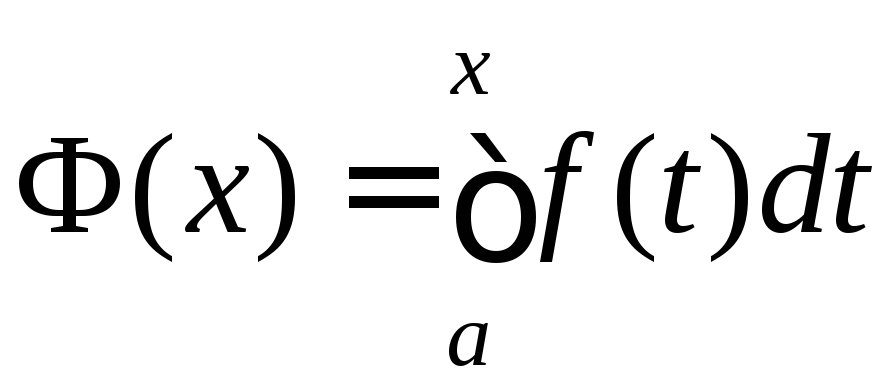 .
.
Означення.
Функція
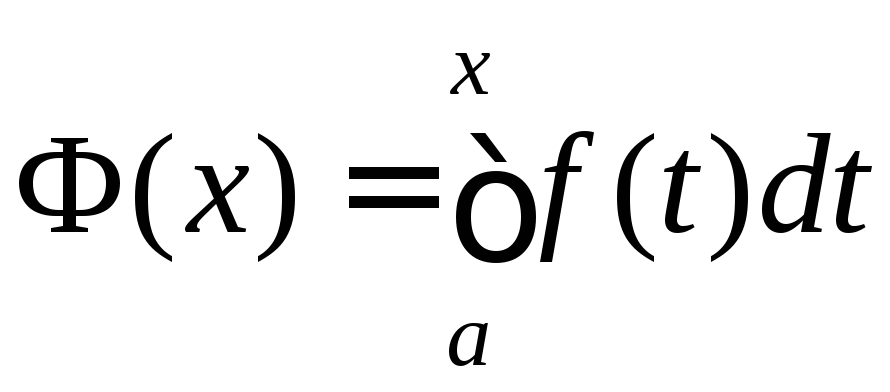 називається інтегралом із змінною
верхньою межею інтегрування.
називається інтегралом із змінною
верхньою межею інтегрування.
Теорема Барроу.
Похідна інтеграла від неперервної функції по змінній верхній межі існує і дорівнює значенню підинтегральної функції в точці, рівній верхній межі:
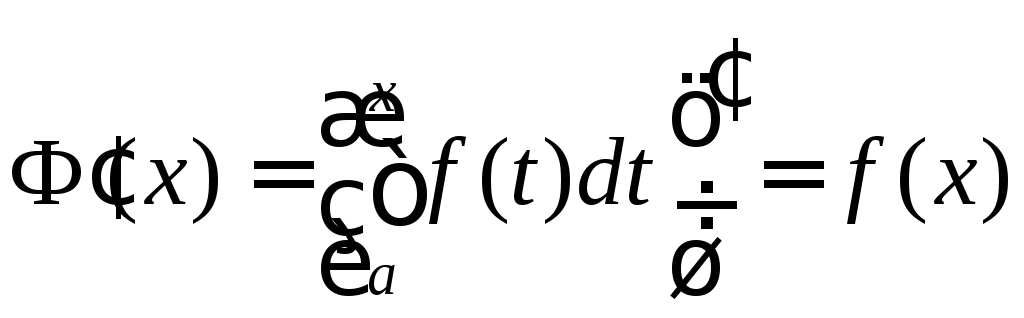 .
.
Таким
чином, функція
![]() є однією з первісних для підинтегральної
функціїf(x).
є однією з первісних для підинтегральної
функціїf(x).
Теорема Барроу вказує на зв’язок між невизначеним і визначеним інтегралами і дає можливість встановити простий метод обчислення визначених інтегралів за формулою Ньютона-Лейбниця.
Формула Ньютона-Лейбниця.
Нехай
F(x)
– будь-яка первісна неперервної функції
![]() на відрізку
на відрізку![]() .
Тоді має місце формула
.
Тоді має місце формула
 .
.
Таким чином, встановлено
Правило. Щоб обчислити визначений інтеграл від будь-якої неперервної функції, треба знайти для неї первісну і скласти різницю значень цієї первісної при верхній та нижній межах інтегрування.
Приклад 2.1. Користуючись формулою Ньютона-Лейбниця, обчислити інтеграли:
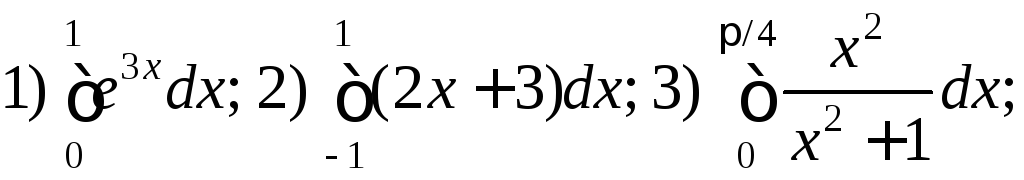
 .
.
Розв’язання.
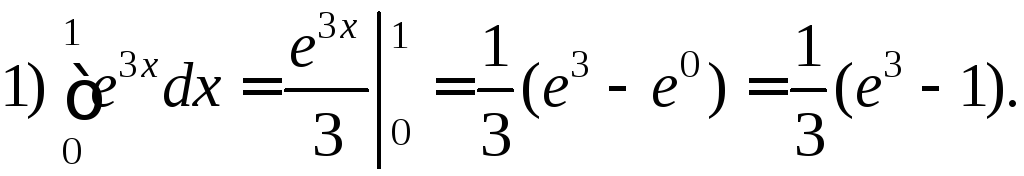
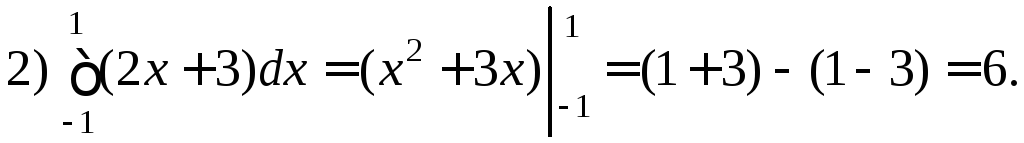
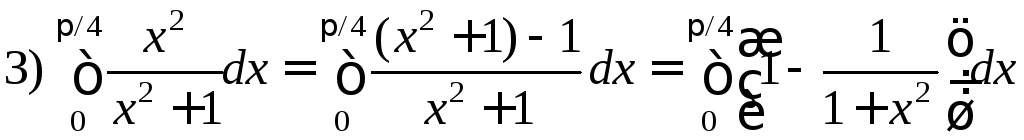 =
=
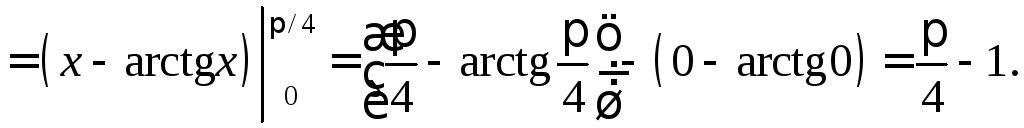
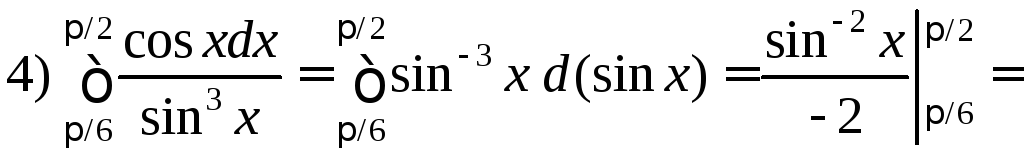
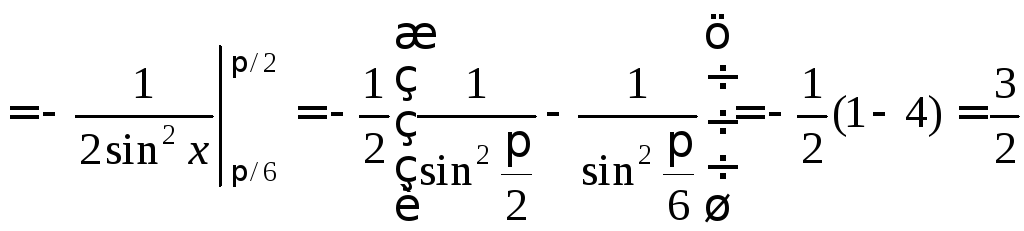 .
.
3. Методи обчислення визначених інтегралів
При обчисленні визначених інтегралів, так же само, як і невизначених інтегралів, використовують методи заміни змінної (підстановки) та інтегрування частинами. Звертаємо увагу на те, що застосування цих двох методів до визначених інтегралів має певні особливості.
3.1. Метод заміни змінної (підстановки)
3.1.1. Підстановка
Теорема
1.
Нехай
потрібно обчислити інтеграл
 ,f(x)
є
неперервною функцією на
,f(x)
є
неперервною функцією на
![]() .
.
Якщо
функція
![]() задовольняє наступні умови:
задовольняє наступні умови:
1. Функція
![]() та її похідна
та її похідна![]() є неперервними функціями на відрізку
є неперервними функціями на відрізку![]() .
.
2. При
зміні t
у
проміжку
![]() значення функції
значення функції![]() не виходять за межі відрізка
не виходять за межі відрізка![]() :
:
![]() .
.
3.
![]()
то справедлива рівність
 (3.1)
(3.1)
Ця формула називається формулою заміни змінної (підстановки) у визначеному інтегралі.
Зауваження
1. Підкреслимо, що відповідно до теореми 1, у визначеному інтегралі крім безпосередньої заміни змінної інтегрування потрібно змінити також межі інтегрування. У зв’язку із цим відпадає необхідність повернення до первісної змінної, обов’язкового у випадку невизначеного інтеграла.
2. Нові межі інтегрування знаходяться наступним чином:
– нижня
межа
![]() знаходиться як розв’язок рівняння
знаходиться як розв’язок рівняння![]() відносно невідомого
відносно невідомого![]() ;
;
– верхня
межа
![]() знаходиться як розв’язок рівняння
знаходиться як розв’язок рівняння![]() відносно
відносно![]() .
.
Якщо
функція
![]() не є монотонною, то може статися, що
зазначені рівняння дадуть кілька різних
пар
не є монотонною, то може статися, що
зазначені рівняння дадуть кілька різних
пар![]() і
і![]() ,
які задовольняють умови теореми 1. В
цьому випадку можна взяти будь-яку з
таких пар.
,
які задовольняють умови теореми 1. В
цьому випадку можна взяти будь-яку з
таких пар.
3. Якщо користуватися формулою (3.1) при невиконанні будь-якої з умов 1–3 теореми 1, то можна одержати неправильний результат.
Приклад 3.1. Обчислити інтеграли

Розв’язання.
1)
Обчислимо
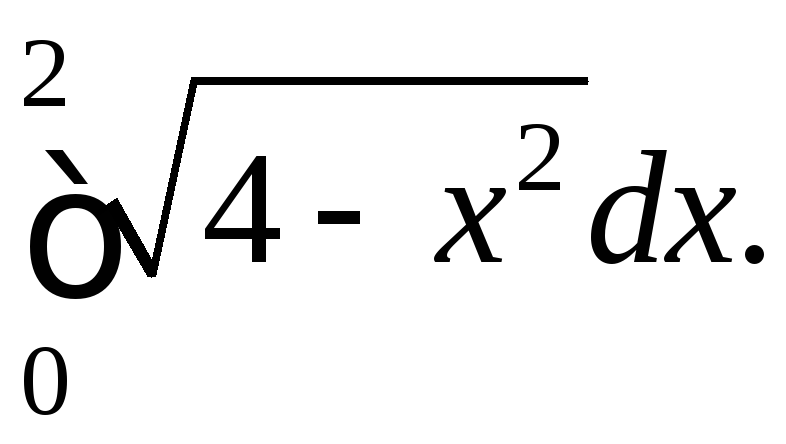
Застосуємо
підстановку
![]() .
.
Тоді
![]() .
Визначимо нові межі інтегрування.
.
Визначимо нові межі інтегрування.
Якщо
нижня межа
![]() ,
то
,
то![]() .
.
З
рівняння
![]() випливає
випливає![]() ,
тобто
,
тобто![]() .
.
Якщо
верхня межа інтегрування
![]() ,
то
,
то![]() .
З рівняння
.
З рівняння![]() випливає
випливає![]() ,
тобто
,
тобто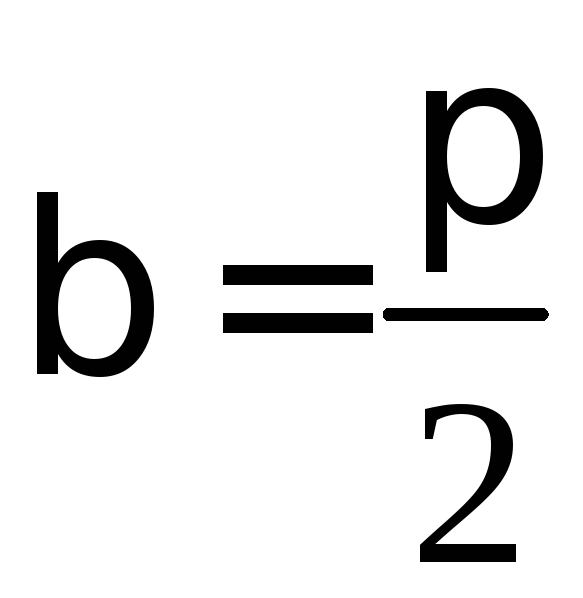 .
.
Переконаємось в законності цієї підстановки, перевіряючи виконання умов теореми 1.
1. Функція
![]() та її похідна
та її похідна![]() є неперервними на відрізку
є неперервними на відрізку .
.
2.
При зміні
![]() на проміжку
на проміжку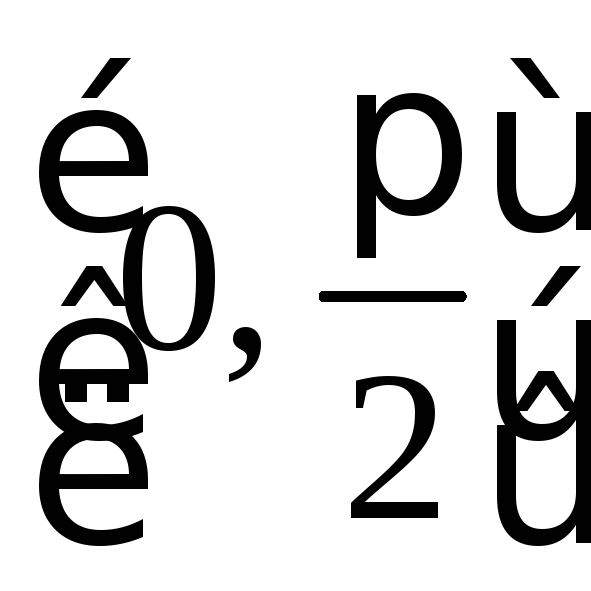 значення функції
значення функції![]() не виходять за межі
не виходять за межі![]() :
:![]() .
.
3. При
цьому
![]() ;
;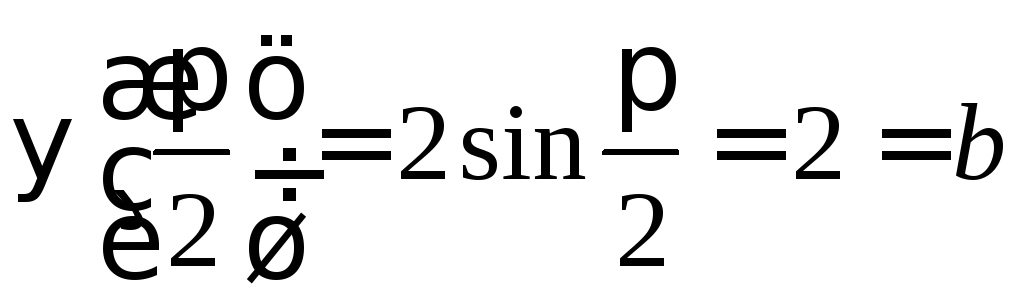 .
.
Тепер
заданий інтеграл
 зі змінною інтегруваннях
зведемо
до інтеграла зі змінною t
і виконаємо інтегрування:
зі змінною інтегруваннях
зведемо
до інтеграла зі змінною t
і виконаємо інтегрування:

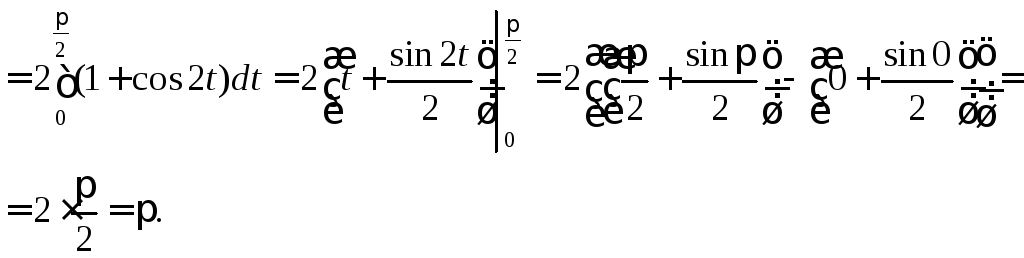
2)
Обчислимо
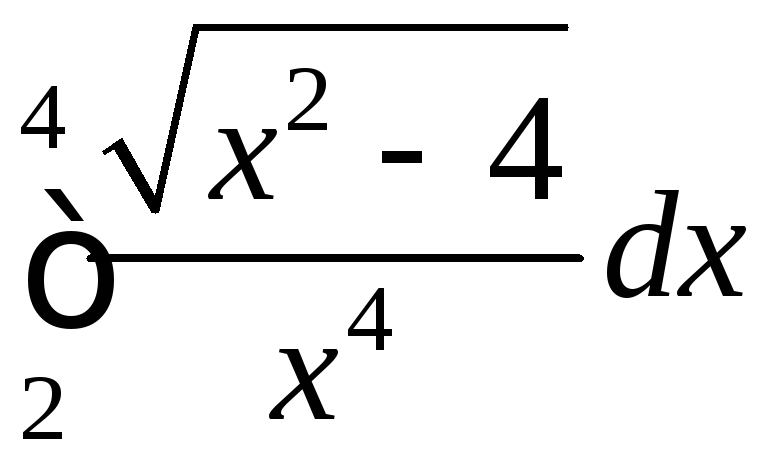 .
.
Застосуємо тригонометричну підстановку:
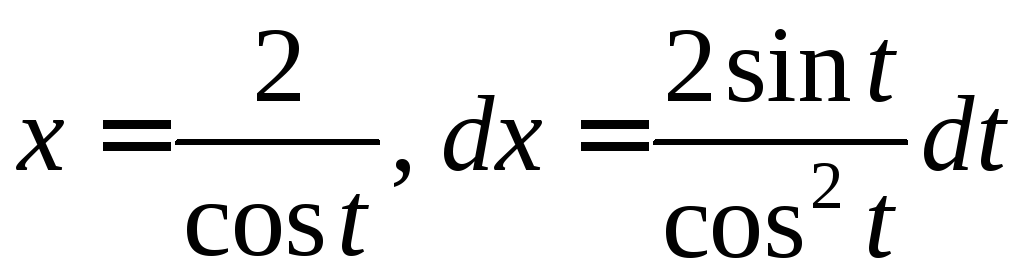 .
.
Визначмо нові межі інтегрування.
Якщо
нижня межа
![]() то
то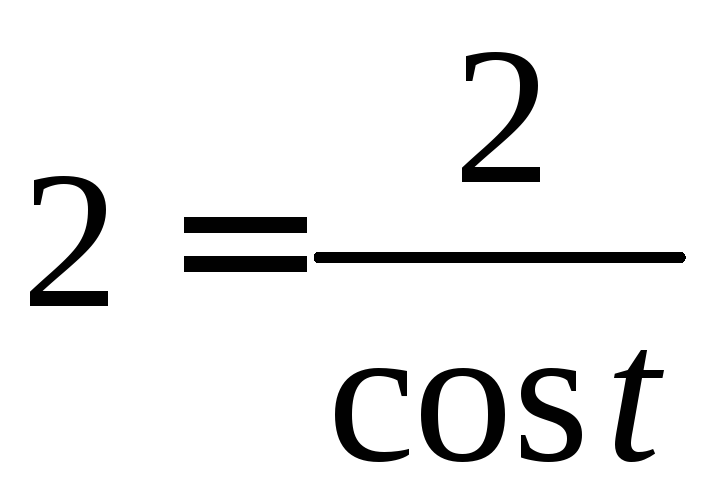 ,
,![]() звідки
звідки![]() тобто
тобто![]() .
.
Якщо
верхня межа
![]() то
то ,
, звідки
звідки тобто
тобто .
.
Переконаємось у законності цієї підстановки.
1. Функція
 та її похідна
та її похідна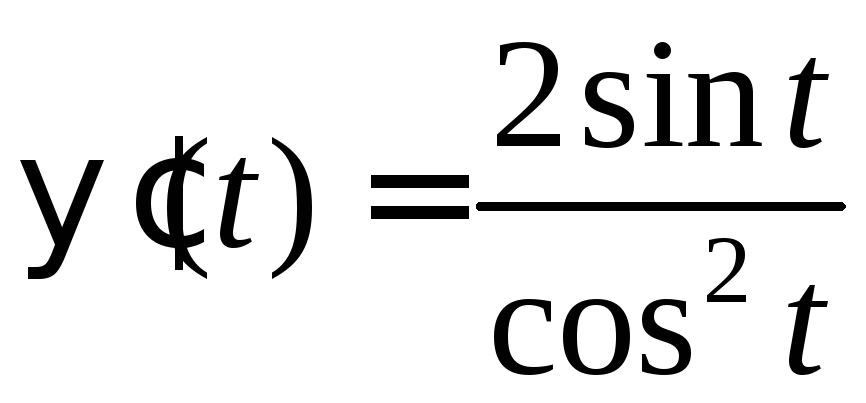 є неперервними на відрізку
є неперервними на відрізку .
.
2.
При зміні
![]() на проміжку
на проміжку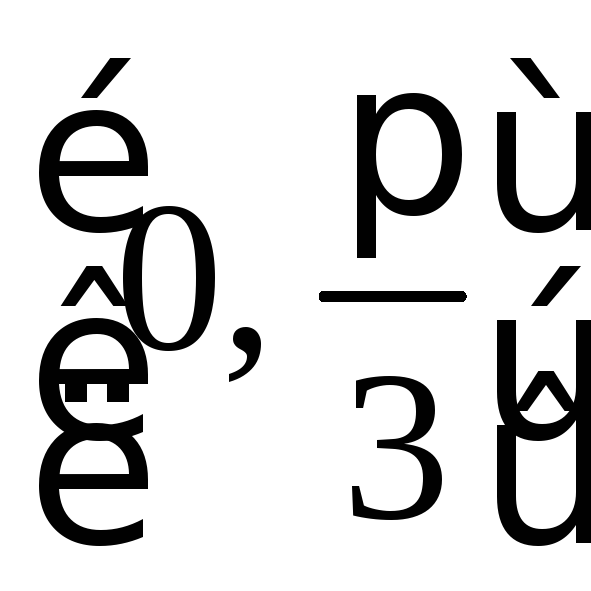 значення функції
значення функції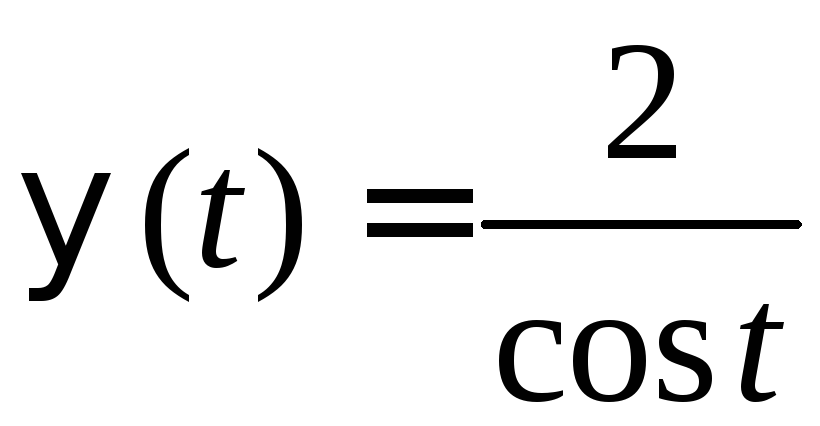 не виходять за межі
не виходять за межі![]() :
:
 .
.
3. При
цьому
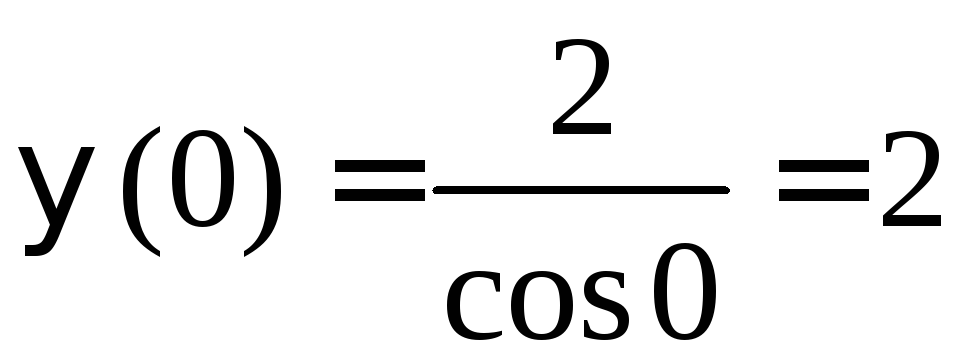 ;
;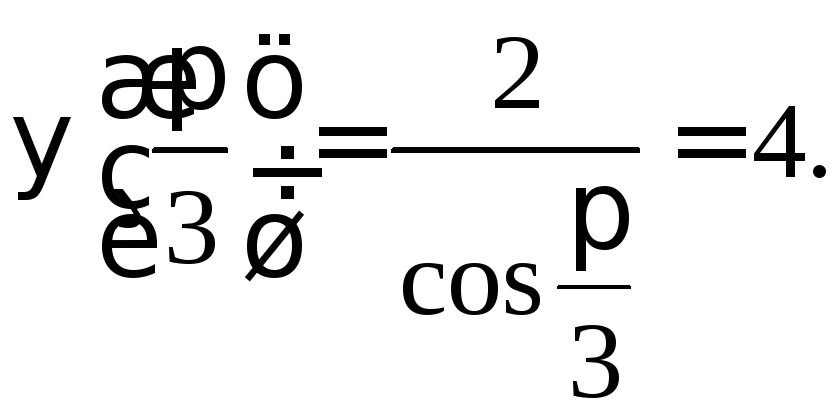
Отже
заданий інтеграл зі змінною інтегрування
х
зведемо до інтеграла зі змінною
![]() і виконаємо інтегрування:
і виконаємо інтегрування:
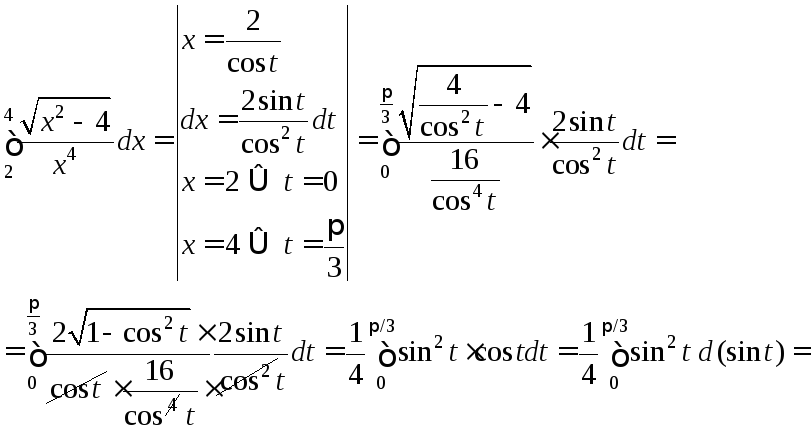
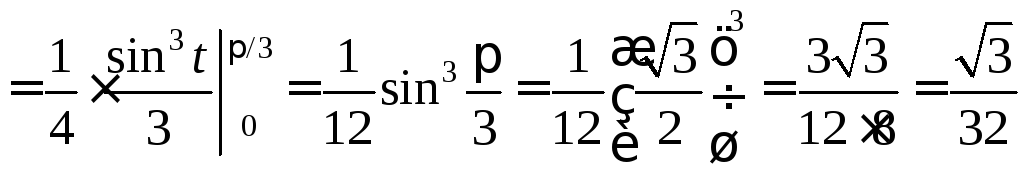 .
.
3)
Обчислимо
 .
.
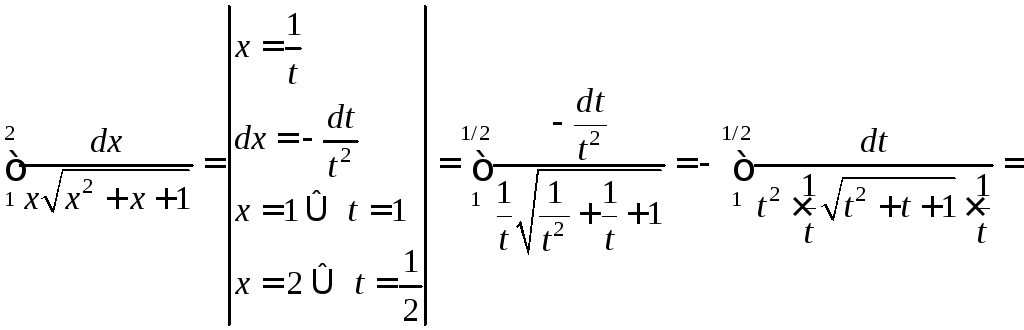
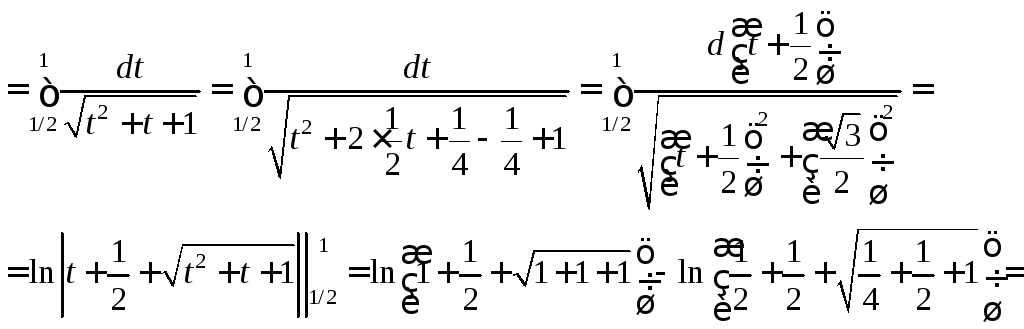
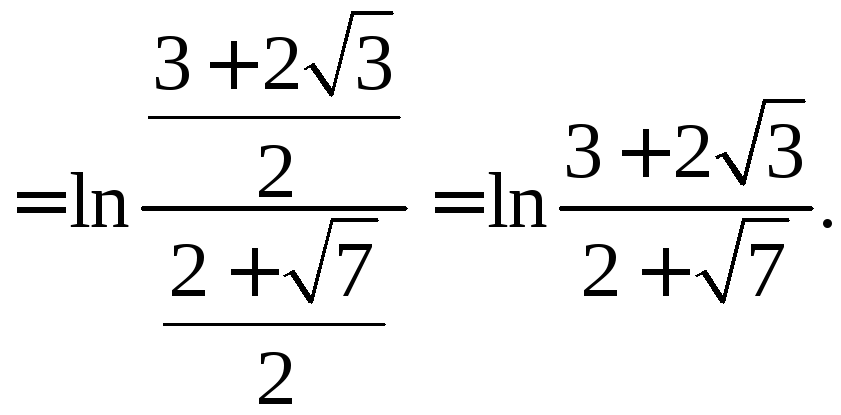
В цьому прикладі обґрунтування законності застосування підстановки слід провести самостійно.
