4.1.2. Параметричне задання кривої

Площа криволінійної трапеції, обмеженої кривою з пара­метричними рівняннями

де є неперервними функціями на відрізку, обчислюється за формулою

(4.7)

Межі інтегрування ізнаходяться як корні рівнянь:

Приклад 4.5. Знайти площу фігури, обмеженої однією аркою циклоїди

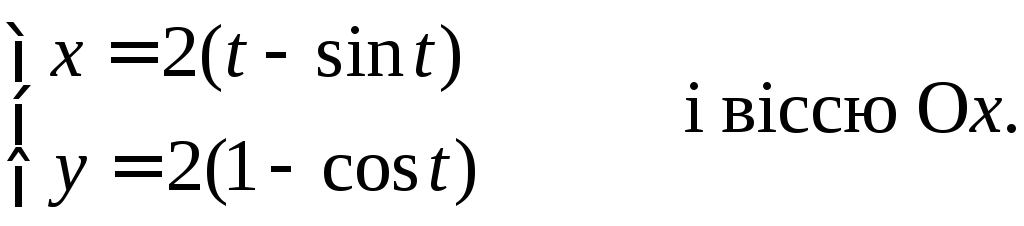
Розв’язання: Першу арку циклоїди матимемо при зміні пара­метра t від 0 до . Складемо таблицю значеньі:

t	0
x	0	0,16	1,14	3,3	6,28	9,26	11,42	12,40	12,56
y	0	0,59	2	3,41	4	3,41	2	0,59	0

За знайденими значеннями побудуємо криву

Рис. 12

Скористуємось формулою (4.7).

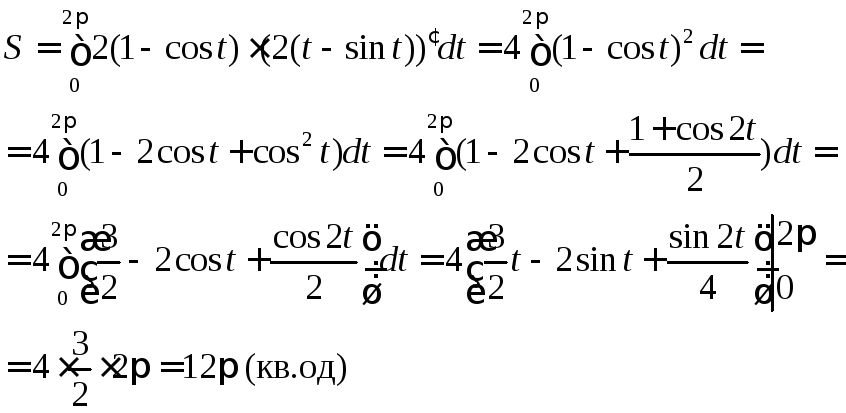
Приклад 4.6. Знайти площу фігури, обмеженої кривою

Розв’язання. Дослідимо криву. Оскільки , то криву розташовано симетрично відносно осіОх.

Складемо таблицю значень t, x, y.

t	–2		–1						2
x	–3		0						–3
y	6		0						–6

При

При

Побудуємо криву за знайденими значеннями.

Рис. 13

Площа петлі одержаної кривої

4.1.3 Задання кривої в полярній системі координат

Площа криволінійного сектора (рис. 14), обмеженого дугою кривої , де– неперервна функція, а також відрізками променіву полярних координатах виражається формулою (4.8):

A

(4.8)

Рис. 14

Приклад 4.7. Знайти площу фігури, обмеженої лемніскатою Бернуллі: .

Розв’язання. Оскільки , то. Знайдемо ті зна­чення, для яких виконується ця нерівність.

.

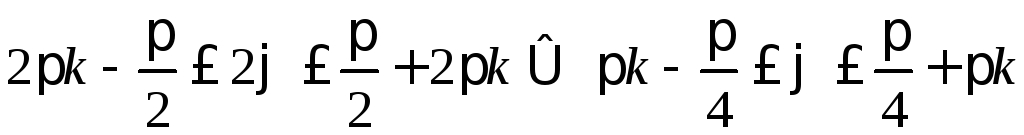
При

при

при – зроблено повний зворот, і значення функції повторюються.

Отже

Складемо таблицю значень для(як відстань від точки кривої до полюса):

	0
	9				0
	3		2,52	2,12	0

Побудуємо графік кривої, враховуючи симетрію відносно координатних осей (в силу парності та – періодичності функції):

Рис. 15

Приклад 4.8. Знайти площу фігури, обмеженої чотири­пелюстковою розою

Розв’язання

Рис. 16

Знайдемо такі значення кута , за яких криваіснує. Оскільки– це відстань від точки кривої до полюса, то. Тому

При:

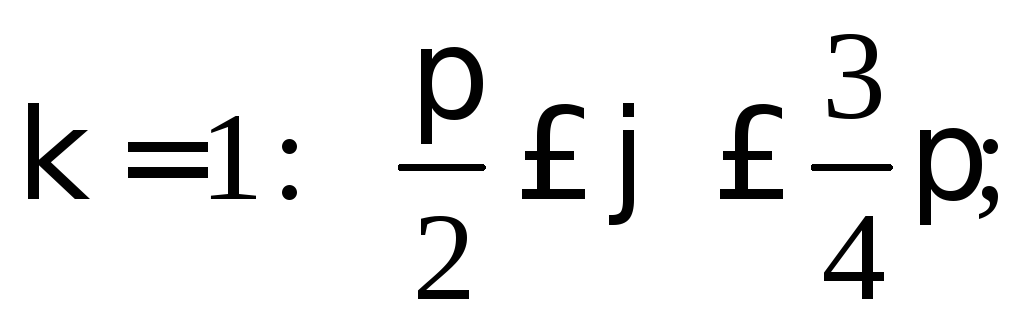
–зроблено повний зворот, і значення функції повторюється.

Функція зростає, коли, і спадає, коли.

Функція має період. Тому крива у кожному з проміжководержується з кривої, розташованої узворотом на, відповідно. Виконаємо рисунок (рис. 16). Щоб знайти площу фігури, яка обмежена кривою,, достатньо обчислити площу пелюст­ка, розташованого в, а потім цей результат помножити на 4.

4.2.Обчислення довжин дуг кривих

4.2.1.Декартова система координат

Якщо криву задано рівняннями , деє неперервними функціями на відрізку, то довжина дуги цієї кривої, що міститься між прямимиобчислюється за формулою (4.9)

Рис. 17

Приклад 4.9. Знайти довжину дуги кривої від точки А(1;2) до точки В (4;4).

Розв’язання. Рівняння кривої задано у декартовій системі координат. Функція є визначеною і неперервною разом із своєю похідноюна відрізку. Тому можна застосувати формулу (4.9).

Рис. 18

Складемо вираз =

Приклад 4.10. Знайти довжину дуги кривої від точки з абсцисоюдо точки з абсцисою.

Розв’язання

Рис. 19

Знайдемо похідну

Обчислимо вираз

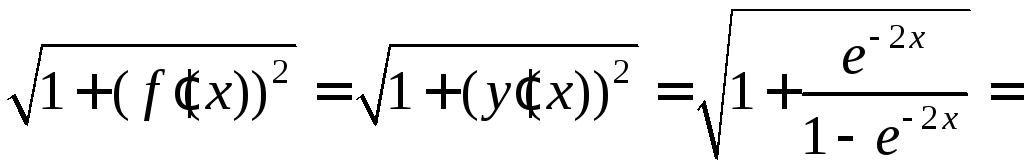
Застосуємо формулу (4.9)