3.1.2. Підстановка

Часто застосовують також підстановку . У цьому випадку нові межі інтегрування визначаються безпосередньо:. Слід мати на увазі, що функція, обернена до функції, має задовольняти всі умови теореми 1.

Приклад 3.2. Обчислити інтеграли

2) ; 3).

Розв’язання

1) Обчислимо

Виконаємо підстановку (заміну змінної): . Нові межі інтегрування визначаються так:.

Нова змінна .

Дійсно, якщо , то(в силу моно­тонного зростання функції. Тобто.

Функція обернення до функціїта її похіднає неперервними на відрізку. Отже умови теореми 1 дотримані.

Інтегруючи одержуємо:

2) Обчислимо .

Застосуємо підстановку (заміну змінної) .

Визначимо нові межі інтегрування: .

Нова змінна . Дійсно, якщото(в силу монотонного зростання функції), тобто

Функція , обернена до функції, та її похіднає неперервними на відрізку. Отже умови теореми 1 дотримані. Переходячи до нової змінної, знайдемо:

3) Обчислимо .

В цьому прикладі обґрунтування законності застосування підстановки слід провести самостійно.

3.1.3. Інтегрування по симетричному проміжку

Застосування метода підстановки дозволяє довести справедли­вість наступних важливих формул щодо інтегрування парних і непарних функцій по симетричним проміжкам:

Отже тепер можна зразу, не виконуючи обчислень, сказати що наприклад, оскільки це інтег­рали по симетричним проміжкам від непарних функцій.

3.2. Метод інтегрування частинами

Формула інтегрування частинами для визначеного інтеграла має вигляд

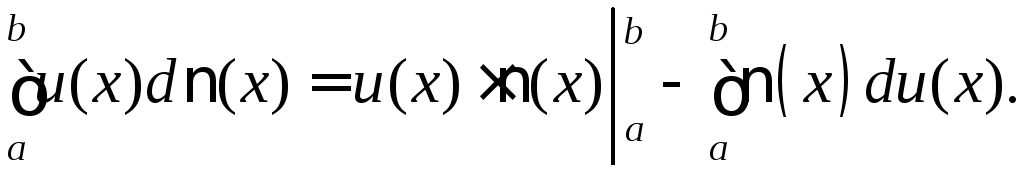
Передбачається, що функції мають на відрізкунеперервні похідні.

Принцип розбиття підинтегрального виразу на множники такий самий, як і для невизначеного інтеграла.

Приклад 3.3. Обчислити інтеграли

Розв’язання

1) Обчислимо

2) Обчислимо

3) Обчислити

4. ОСНОВНІ ГЕОМЕТРИЧНІ ЗАСТОСУВАННЯ ВИЗНАЧЕНОГО ІНТЕГРАЛА

4.1. Обчислення площ плоских фігур

4.1.1. Декартова система координат

Геометричний зміст визначеного інтеграла.

Якщо функція є неперервною на відрізкуто визначений інтегралявляє собою площу криволінійної тра­пеції – фігури, обмеженої лініями,(рис 1):

Якщо , то фігура, обмежена лініями(рис. 2) не є криволінійною трапецією. Площа цієї фігури дорівнює.

Тоді за формулою (4.1) маємо

x

Формули (4.1) і (4.2) можна об’єднати в одну:

(4.3)

Якщо функція на відрізкускінченне число разів змінює знак (рис. 3), то за формулою (4.3) маємо:

y

x

b

d

c

0

a

Рис. 3

(4.4)

Приклад 4.1. Знайти площі фігур, обмежених даними лініями:

а) параболою прямимиі віссю абсцис;

б) параболою прямоюі осями координат.

Розв’язання

а) Виконаємо (рис. 4).

Рис. 4

Застосуємо формулу (4.1). Одержимо

б) Виконаємо рисунок (рис. 5).

Рис. 5

Функція на відрізкузмінює знак, а саме:Для знаход­ження шуканої площіS скористаємося формулою (4.4):

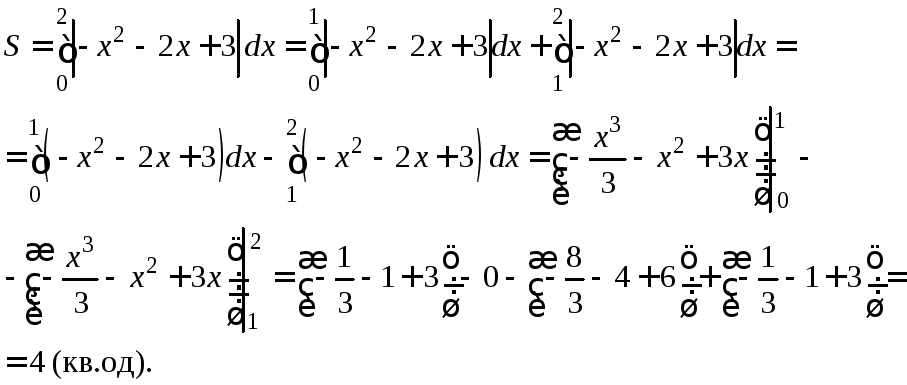
Якщо плоска фігура обмежена двома неперервними кривими іи двома вертикальними прямими(рис. 4), то її площа обчислюється за формулою (4.5):

Рис. 6

. (4.5)

Приклад 4.2. Знайти площу фігури, обмеженої даними лініями:

.

Розв’язання. Для того, щоб обчислити площу заданої фігури, необхідно:

а) побудувати плоску фігуру, обмежену заданими лініями;

б) визначити межі інтегрування;

в) обчислити відповідний визначений інтеграл.

Рис. 7

Виконаємо рисунок (рис. 7). Рівняння верхньої лінії нижньої лініїВизначимо межі інтегру­вання. Для цього обчислимо абсциси точок перетину прямоїі параболи.

.

За формулою (4.5):

Якщо плоска фігура має складнішу форму (рис. 8), то пря­мими, паралельними оси ОY, її треба розбити на скінчену суму фігур, площі яких знаходяться за формулою (4.5). Тоді площа S дорівнюватиме сумі знайдених площ фігур (на рис. 8 ).

Рис. 8

Приклад 4.3. Знайти площу фігури, обмеженої даними лініями:

Розв’язання

Рис. 9

Виконаємо рисунок (рис. 9). Знайдемо абсциси точок перетину ліній, що обмежують фігуру.

Лінії іперети­наються у точці (0;0).

Щоб знайти абсцису точки перетину ліній і, розв’яжемо рівняння

Отже абсциса точки перетину цих ліній x=4.

Абсциса точки перетину ліній івизначається з рівняння:

Запишемо рівняння верхньої ліній що обмежують фігуру:

Оскільки нижня лінія задається при різних значеннях х різними аналітичними виразами, розіб’ємо фігуру на дві частини прямою . Застосовуючи формулу (4.5), одержимо:

Якщо криволінійна трапеція обмежена лініями (рис. 10) то формула для обчислення її площі має вигляд (4.6):

Приклад 4.4. Знайти площу фігури, обмеженої лініями

Розв’язання. Виконаємо рисунок (рис. 11).

Рис. 11

–2