
- •1.Несобственные интегралы и их свойства.
- •3. Абсолютная сходимость несобственных интегралов. Признак сравнения сходимости ни.
- •4.Предельный признак сравнения
- •6.Признак Абеля
- •7. Метрическое пространство . Некоторые топологические понятия
- •8.Евклидово пространство .
- •9. Последовательности точек пространства .
- •10. Предел отображения.
- •11. Предел по направлению. Повторные пределы.
- •12.Локальные свойства непрерывных отображений.
- •13.Глобальные свойства непрерывных отображений.
- •14. Линейные отображения.
- •15. Дифференцируемые отображения.
- •16.Свойства дифференцируемых отображений.
- •17. Достаточное условие дифференцируемости функций многих переменных.
- •18.Производная по направлению. Градиент.
- •19. Частные производные высших порядков.
- •20.Формула Тейлора для функций многих переменных.
- •21. Необходимые условия экстремума.
- •22. Достаточные условия локального экстремума.
- •23. Неявные функции.
- •24. Обратное отображение.
- •25. Необходимые условия зависимости функций.
- •26. Достаточные условия зависимости функций.
- •27. Понятие условного экстремума.
- •28. Метод множителей Лагранжа.
- •29. Числовые ряды. Критерий Коши
- •30.Признаки сравнения сходимости числовых рядов.
- •31. Признаки Даламбера и Коши сходимости рядов.
- •32. Интегральный признак сходимости ряда.
- •33. Знакочередующиеся ряды.
- •34.Признак Абеля и Дирихле.
- •35. Абсолютно и условно сходящиеся числовые ряды
- •36. Перемножение абсолютно сходящихся числовых рядов.
- •37. Бесконечные произведения.
- •38. Равномерная сходимость функциональных рядов и последовательностей.
- •39.Признаки равномерной сходимости функц. Рядов.
- •41. Непрерывность суммы ряда.
- •42.Интегрирование равномерно сходящихся рядов и последовательностей
- •43. Дифференцирование равномерно сходящихся рядов.
- •44. Степенной ряд, радиус сходимости.
- •45. Формула Коши-Адамара
- •46.Почленное дифференцирование и интегрирование степенных рядов.
- •47. Аналитические функции. Ряд Тейлора.
- •48. Ряды Тейлора основных элементарных функций.
- •49.Ряды Фурье по ортонормированной системе функций.
- •50. Интеграл Дирихле.
- •51. Сходимость рядов Фурье в точке(лемма 1)
- •52. Признак Дини и следствия из него
- •53. Суммирование рядов Фурье методом средних арифметических.
- •54. Теорема Фейера.
- •55. Теорема Вейерштрасса.
- •56. Неравенство Бесселя. Равенство Парсеваля.
- •57.Диф. Тригонометрических рядов Фурье.
- •58. Интегрирование рядов Фурье
- •59.Комплексная форма ряда Фурье.
26. Достаточные условия зависимости функций.
Теорема
15.
Пусть
все миноры s+
1 порядка
матрицы Якоби (3)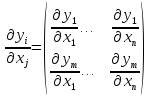 системы функций
системы функций
yi=fi(x),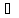 x
€ G,
i
= 1,m.(1)
равны
0 в каждой точке открытого множества G
и хотя бы один из миноров порядка s(s<m<=
n)
не равен 0 в некоторой точке a€G,
тогда функции, содержащиеся в этом
миноре независимы на множестве G,
и существует некоторая окрестность
точки a
такая, что остальные m—s
функций системы (1) зависят на этой
окрестности от s
указанных функций.
x
€ G,
i
= 1,m.(1)
равны
0 в каждой точке открытого множества G
и хотя бы один из миноров порядка s(s<m<=
n)
не равен 0 в некоторой точке a€G,
тогда функции, содержащиеся в этом
миноре независимы на множестве G,
и существует некоторая окрестность
точки a
такая, что остальные m—s
функций системы (1) зависят на этой
окрестности от s
указанных функций.
Доказательство.
Не
нарушая общности рассуждений, можем
считать, что неравный нулю в точке aминор
s-го
порядка расположен в левом верхнем углу
матрицы (3). Следовательно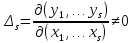 (4)
в
точке a.
В силу теоремы о неявной функции и
условия (4) из первых уравнений системы
(1) найдем x1=
(4)
в
точке a.
В силу теоремы о неявной функции и
условия (4) из первых уравнений системы
(1) найдем x1= 1(
1( )xs=
)xs= s(
s( ),где
),где
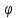 i,
i=1,s
непрерывно
дифференцируемые функции в некоторой
окрестности Uточки
(b1,...,bs,as+1,...,an),
Ьi=
fi(a),i=
1, s.
Подставим xi,
i=
1, sв
последниеm—
sуравнений
(1). Имеем yl=Fl(
i,
i=1,s
непрерывно
дифференцируемые функции в некоторой
окрестности Uточки
(b1,...,bs,as+1,...,an),
Ьi=
fi(a),i=
1, s.
Подставим xi,
i=
1, sв
последниеm—
sуравнений
(1). Имеем yl=Fl( 1,…,
1,…, s;xs+1,…,xn),
l=s+1,m
s;xs+1,…,xn),
l=s+1,m
Поскольку
имеет место условие (4), то из следствия
2 следует, что функции yi=
fi(x),
i=1,s
независимы
на множестве G.
Покажем, что остальные m-s
функций
системы (1) зависят от указанных sфункций
в окрестности U.
Для этого достаточно убедиться в том,
что непрерывно дифференцируемые функции
Fl(l>s)
не
зависят от переменных xs+1,...,
xn.
Следовательно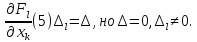 В итоге (5)=0,k=s+1,n
В итоге (5)=0,k=s+1,n
27. Понятие условного экстремума.
Определение1. Точка aϵE называется точкой условного экстремума функции f относительно уравнений связи
Fi(x)=0,
i=1,m
(1), если
она является точкой локального экстремума
функции
 E.
E.
Возьмем,
что функции f:G→R,
Fi:
G→R,
i=1,m,
GʗRn
непрерывно дифференцируемы на открытом
множестве G,
и ранг матрицы (
 ),i=1,m,
j=1,n,
aϵE
равен m.
Это означает, что функция Fi,
i=1,m
независимы на множестве G.
Для определенности положим, что
),i=1,m,
j=1,n,
aϵE
равен m.
Это означает, что функция Fi,
i=1,m
независимы на множестве G.
Для определенности положим, что
 ≠0
в точке а. Тогда из (1) по теореме о неявной
функции найдем
≠0
в точке а. Тогда из (1) по теореме о неявной
функции найдем
x1=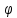 1(
1(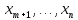 )
…xm=
)
…xm= m(
m(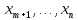 ),(2)
),(2)
где
 i,
i=1,m
непрерывно
дифференцируемые функции в некоторой
окрестности точки a=(am+1,…,an).
Подставим x1,..,xm
из (2) в f(
i,
i=1,m
непрерывно
дифференцируемые функции в некоторой
окрестности точки a=(am+1,…,an).
Подставим x1,..,xm
из (2) в f( ),
получим
),
получим
g( )=
f(
)=
f( )
)
непрерывно дифференцируемые функции в некоторой окрестности точки а. Т.к. условия (1) и (2) равносильны, то имеет место утверждение:
Точка
aϵE
является точкой условного экстремума
функции f
относительно уравнений связи (1)тогда
и только тогда, когда
a
является точкой локального экстремума
функции
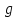 .
.
Это метод – метод исключения части переменных.
28. Метод множителей Лагранжа.
Рассмотрим функцию
L(x)=f(x)+ (1)
(1)
Функция L(x)=L(x;⋋) называется функцией Лагранжа, а числа ⋋1,…,⋋m называются множителями Лагранжа. Из
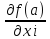 =
= следует dL(a)=0,
которое означает, что если а точка
условного экстремума функции f
относительно уравнений связи Fi(x)=0,
i=1,m
, то она является стационарной точкой
функции Лагранжа L(x).
Таким образом, для нахождения точки а,
подозрительной на экстремум, необходимо
построить функцию Лагранжа (1) с
неопределенными коэффициентами ⋋1,…,⋋m.
Из системы
следует dL(a)=0,
которое означает, что если а точка
условного экстремума функции f
относительно уравнений связи Fi(x)=0,
i=1,m
, то она является стационарной точкой
функции Лагранжа L(x).
Таким образом, для нахождения точки а,
подозрительной на экстремум, необходимо
построить функцию Лагранжа (1) с
неопределенными коэффициентами ⋋1,…,⋋m.
Из системы
 =0,
=0,
 ,
, =0,j=1,m
(2)
найти решение (a1,..,an,
⋋1,…,⋋m).
Тем самым будет найдена точка (a1,..,an).
Если при этом окажется, что система (2)
дает возможность непосредственно найти
а, не вычисляя ⋋j,
j=1,m
, то с точки зрения исходной задачи это
и надо делать.
=0,j=1,m
(2)
найти решение (a1,..,an,
⋋1,…,⋋m).
Тем самым будет найдена точка (a1,..,an).
Если при этом окажется, что система (2)
дает возможность непосредственно найти
а, не вычисляя ⋋j,
j=1,m
, то с точки зрения исходной задачи это
и надо делать.
