Програма stat Cтатистична обробка результатів вимірювань

1. Мета розрахунків

Програма виконує статистичну обробку експериментальних даних вимірювання одного параметра, в умовах, коли систематичні помилки відсутні і діють тільки фактори, коли помилки можна вважати випадковими. Тоді можна прийняти, що розподіл випадкових помилок при вимірюваннях підлягає нормальному закону розподілу Гаусса, і визначити головні статистичні характеристики вибірки даних - середнє значення вимірюваного параметра Х, дисперсію ², середньоквадратичне відхилення , тощо.

Нормальний закон розподілу Гаусса придатний для аналізу даних при їх достатньо великій кількості,   30.

2. Алгоритм.

Всі статистичні характеристики введеного числового ряду (вибірки) в програмі підраховуються за простими формулами, які можна знайти в спеціальній літературі [ ] . Тому далі дамо лише коротке пояснення найважливіших термінів та понять математичної статистики та теорії вірогідності, які тут використовуються і необхідні для того, щоб раціонально обирати вхідні і правильно оцінювати вихідні параметри роботи програми, робити аргументовані висновки з результатів статистичної обробки даних.

Генеральна сукупність - необмежений ряд значень величини в в N   вимірюваннях. Це теоретичне поняття теорії вірогідності. Математична статистика має справу з обмеженими вибірками даних, які в деякій мірі (тобто частково, з деякою вірогідністю) адекватно характеризують генеральну сукупність. В інших випадках генеральна сукупність може бути обмеженою, але досить великою сукупністю, яку досліджують, обираючи деяку відносно невелику групу даних (результатів вимірювань).

Для генеральної сукупності деякі поняття і параметри математичної статистики асимптотично наближаються до понять і параметрів теорії вірогідності.

Вибірка - обмежений ряд випадкових значень в n=1…N вимірюваннях, об”єкт аналізу математичної статистики.

Виміряне значення величини в одному n–ному “досліді” - .

Істинне (справжнє) значення вимірюваної величини (невідоме) -.

Похибка вимірювання (абсолютна)

. (1)

Похибка вимірювання (відносна)

, або в % - (2)

Середнє арифметичне значення вимірюваної величини, є статистичною оцінкою невідомого істинного (або справжнього) значення вимірюваної величини :

, . (3)

Середньоквадратичне відхилення вимірюваної величини від середнього арифметичного – одна з найважливіших характристик вибірки, визначається за формулою Бесселя

. (4)

Цей параметр характеризує ступінь концентрації результатів вимірювань навкруги середнього арифметичного.

Слід звернути увагу на те, що параметр практично не залежить від кількості вимірювань - він характеризує лише похибку даного фізичного методу вимірювань, і його вказують саме як технічну (стандартну) характеристику експериментального методу. Цю величину називають також “вибірковий стандарт”, “емпіричний стандарт” або просто “стандарт”.

Квадрат середньоквадратичного відхилення має назву “дисперсія”:

. (5)

Середньоарифметична помилка. Інколи користуються також поняттям середньоарифметичної помилки, яка має простіший і зрозуміліший зміст і підраховується за простішими формулами:

. . (6)

При великих N вони дають практично однаковий результат. При малих N кращий результат дає друга формула.

При великих N між середньоквадратичним і середньоарифметичним відхиленням (помилкою) існує простий зв”язок:

. (7)

Якщо співвідношення між значеннями відхилень, підрахованих за формулами (4) та (6) суттєво відрізняються від (7), це означатиме, що нормальний закон розподілу помилок в даному випадку не зовсім придатний, а результати оцінювання статистичних характеристик ненадійні. Тому порівняння Δ_Х та _Х можна розглядати як приблизний спосіб оцінювання якості виконаного статистичного аналізу.

Середньоквадратичне відхилення (помилка) середнього арифметичного – дає оцінку похибки результата вимірювань, тобто того числа (середнє арифметичне Х_СА) , яке одержують після всіх N вимірювань даної вибірки. Тому ця помилка, на відміну від , буде тим меншою (а кінцевий результат вимірювань Х_СА – тим точніший), чим більша кількість вимірювань:

. (8)

Коефіцієнт варіації (коваріація) – відносна (безрозмірна) величина середньоквадратичної помилки в частках одиниці або в % :

, . (9)

Довірчий інтервал для середнього арифметичного. Головні статистичні параметри вибірки, обговорені вище, і в першу чергу – середнє арифметичне , фактично досягають своїх точних значень лише при умові необмежених вибірок, тобто при . Тоді результат вимірювання можна подати в формі

, (10)

де  - відхилення, причому теорія вказує точне значення вірогідності , яке відповідає будь-якому відхиленню. Наприклад, вірогідність того, що значення Х_СА існує в заданому інтервалі , складає для деяких окремих інтервалів (із значеннями 1, 2, 3) :

інтервал -   68.3%

інтервал -   98.5% (11)

інтервал -   99.7%.

Інтервал між двома граничними числами та , які дає формула (10), називають довірчим інтервалом середнього арифметичного.

Проте в обмежених вибірках, особливо з невеликими N, помилка визначення Х_СА зростає, або інакше – розширюється довірчий інтервал ( ширина +-(-)=2) , в який з заданою вірогідністю  попадає значення Х_СА. Тому для обмежених вибірок з невеликими N прийнято більш точно визначати відхилення  за допомогою додаткових коефіцієнтів Стьюдента t_S>1 . Результат вимірювання в таких випадках можна записати так:

. (12)

Для визначення коефіцієнтів Стьюдента , які залежать від двох параметрів – довірчої вірогідності  та кількості вимірювань N, існують спеціальні таблиці .

Необхідна кількість вимірювань N. При невеликій кількості вимірювань помилка, яка є випадковою величиною, може бути значною. Для зменшення помилки вимірювання є лише два шляхи – або підвищувати точність самого фізичного методу (тобто зменшити _Х) , або збільшувати кількість вимірювань N (тобто зменшувати величину ).

При плануванні дослідів (вимірювань) доцільно спочатку оцінити необхідну кількість вимірювань для того, щоб досягти бажаної надійності результата. Для цього можна користуватись таблицею, яка вказує залежність між надійністю (вірогідністю ) визначення середньоквадратичної помилки _ХСА середнього арифметичного та необхідною для цього кількістю вимірювань:

Помилка відносна ХХСА	=0.500	=0.700	=0.900	=0.950	=0.990	=0.999
1.0	2	3	5	7	11	17
0.5	3	6	13	18	31	50
0.4	4	8	19	27	46	74
0.3	6	13	32	46	78	130
0.2	13	29	70	100	170	280
0.1	47	110	270	390	700	1100
0.05	180	430	1100	1500	2700	4300
0.01	4500	1100	27000	38000	66000	110000

Наприклад, для того, щоб помилка кожного окремого (одного) вимірювання _Х складала величину не більше 1_ХСА з вірогідністю 99%, потрібно виконати N=11 вимірювань. Якщо ж вимірювань тільки N=2, тоді вірогідність того, що результат вимірювань попадає в інтервал складає 50% ( тобто з однаковою 50%-ю вірогідністю можна вважати що результат попадає або ж не попадає у вказаний інтервал) .

Якщо кількість вимірювань N відома і доповнити її вже неможливо, наведена таблиця дасть змогу орієнтовно оцінити фактичну вірогідність  формули з заданим значенням  = const_XCA.

Гістограма . Якщо інтервал між найбільшим і найменшим значенням виміряної величини Х, поділити на декілька (М) менших частин з розміром , і розподілити результати всіх вимірювань в окремі групи , , і т.д., можна підрахувати кількість чисел з повної вибірки N, які попали в кожну з частин ( кожний інтервал ₂ ) :

(13)

Числа N₁….N_M графічно відображують в формі гістограми, показаної на рис.1а, на якій висота кожного прямокутника шириною ₂ дорівнює відповідному значенню N₁, N₂,…N_M.

Функція густини розподілу випадкових помилок. При необмеженій кількості вимірювань і зростанні кількості інтервалів їх ширина на гістограмі відповідно зменшується, ₂0. Якщо через вершини таких прямокутників на рис.1 провести лінію, гістограма набуває специфічної форми, показаної на рис.2. Це є об”єкт теорії вірогідності - функція густини розподілу випадкових помилок для безперервної величини Х (для нормального розподілу - функція Гаусса):

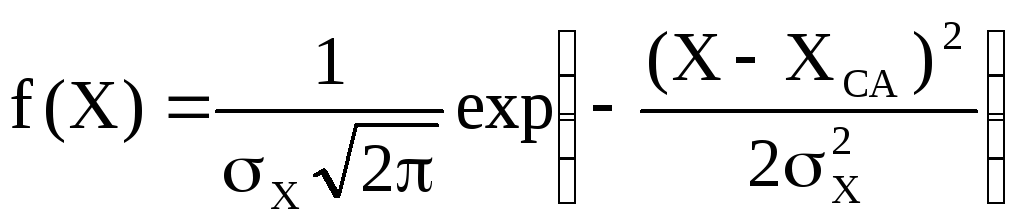. (14)

Ця формула виведена на основі трьох положень:

1. помилки вимірювань можуть приймати безперервний ряд значень;

2. однакові помилки з різними знаками зустрічаються однаково часто;

3. чим більша величина помилки, тим вірогідність її появи менша.

Звідси зрозуміла форма функції f(X) - з максимумом в середній точці Х=Х_СА і експоненційним зменшенням до нуля при зростанні помилки обох знаків (Х-Х_СА) .

Значення функції в точці максимума дорівнює множнику перед експонентою, а в точках - дорівнює .

Площа під всією необмеженою (Х= - …+) кривою Гаусса дорівнює одиниці – це вірогідність того, що випадкове значення вимірюваної величини попадає в інтервал -…+. Площа заштрихованої ділянки на рис.2 , яка дорівнює

(15)

-це вірогідність  0.683 того, що випадковий результат вимірювання попаде в інтервал