
- •Содержание
- •Введение
- •1.Обзор работ по резонансным ударно-вибрационным машинам
- •1.1 Общие сведения о виброуплотняющих машинах и областях их применения
- •1.2 Динамика резонансных ударно-вибрационных машин
- •2. Анализ динамики ударно-вибрационных систем
- •2.1 Обоснование расчетной схемы ударно-вибрационной системы с двумя степенями свободы на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами
- •2.2 Динамика ударно-вибрационной системы с двумя степенями свободы, на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами
- •2.3 Анализ результатов исследования динамики вибрационной системы с двумя степенями свободы, на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами.
- •Выводы по разделу
- •3. Методика расчета двухмассной резонансной ударно-вибрационной системы с двумя степенями свободы
- •3.1 Расчет резонансной ударно-вибрационной системы с двумя степенями свободы, на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами.
- •3.2 Выводы по разделу
- •Заключение
2.2 Динамика ударно-вибрационной системы с двумя степенями свободы, на примере резонансной виброплощадки с центробежным и эксцентриково-шатунным приводами
Уравнение движения ударно-вибрационной площадки с двумя степенями свободы имеет различный вид в зависимости от того, включился или не включился упругий ограничитель.
Для расчетной схемы ударно-вибрационной площадки с центробежным приводом (рис. 5), дифференциальные уравнения движения будут иметь вид:
(25)

при

 (26)
(26)
при

Точкой обозначено дифференцирование по времени.
Для расчетной схемы с эксцентриково-шатунным приводом (рис. 6), дифференциальные уравнения движения будем иметь вид:
 (27)
(27)
при

 (28)
(28)
при

Точкой обозначено дифференцирование по времени.
Как уже отмечалось, такие системы называют кусочно-линейными. Движение кусочно-линейной системы состоит из чередующихся этапов. На каждом из этих этапов движение системы описывается линейными дифференциальными уравнениями. При изучении динамики ударно-вибрационных машин интерес представляют периодические движения. В реальных системах такие движения быстро устанавливаются благодаря наличию больших диссипативных сопротивлений. Параметры периодических движений - размах колебаний, экстремальные значения ускорений, фазовые соотношения, являются основными характеристиками таких машин.
Однако аналитическое определение даже простейших периодических решений для кусочно-линейных систем (в нашем случае с одним ударом об ограничитель за один период вынуждающей силы) очень затруднено.
Обычно применяемый для этих целей метод припасовывания [17] приводит к сложным трансцендентным уравнениям, выражающим условия периодичности. Кроме того, он требует предварительного построения последовательности этапов, а также исследования существования устойчивости полученного результата.
Приближенные методы, например метод гармонического баланса [17], дает недостаточную информацию, а также требует громоздких вычислений. Границы их применимости четко не устанавливаются.
Практически наиболее удобным способом нахождения периодических нелинейных движений, в частности кусочно-линейных систем, является математическое моделирование. Численное интегрирование дифференциальных уравнений движения с помощью компьютерного моделирования с последующим выделением периодического движения автоматически собирает устойчивые решения и позволяет найти все необходимые характеристики.
Для исследования одноударных периодических режимов вибрационных машин разработана компьютерная программа. Программа осуществляет численное интегрирование кусочно-линейных уравнений (25), (26) выделяет одноударные периодические решения и вычисляет параметры периодического движения схемы.
На (рис. 7), представлена блок-схема программы расчета периодических движений для двухмассной ударно-вибрационной системы.

Рис. 7 Блок-схема программы расчета периодических движений
Следующий
блок осуществляет преобразования,
необходимые для приведения уравнений
к единому виду. Вводятся безразмерные
переменные - время и перемещение. Тем
самым устраняется возможная проблема
разно масштабности переменных. Далее
задаются стандартные начальные условия,
соответствующие наличию положительного
расстояния между массами
 и
и и
параметры, необходимые для начала
интегрирования.
и
параметры, необходимые для начала
интегрирования.
Численное интегрирование уравнений движения производится при помощи программы, реализующей метод Адамса - переменного шага и порядка [26]. Шаг интегрирования автоматически выбирается максимально возможным, исходя из заданной точности и текущего состояния системы, что обеспечивает высокую эффективность метода.
Возможны
два типа движения масс
 и
и ,
раздельные и совместные. Тип движения
определяется законом относительного
перемещения:
,
раздельные и совместные. Тип движения
определяется законом относительного
перемещения:

(29)
После
каждого шага интегрирования вычисляется
 .
Если на выполненном шаге знак этой
величины изменяется, то производится
интерполяционное уточнение момента
смены знака и вычисление состояния
системы (то есть координат и скоростей),
соответствующего этому моменту. После
чего интегрирование продолжается, но
уже для нового типа движения. Для
интерполяции используется подпрограммаINTRP
[26].
.
Если на выполненном шаге знак этой
величины изменяется, то производится
интерполяционное уточнение момента
смены знака и вычисление состояния
системы (то есть координат и скоростей),
соответствующего этому моменту. После
чего интегрирование продолжается, но
уже для нового типа движения. Для
интерполяции используется подпрограммаINTRP
[26].
Задачей
расчета является определение параметров
периодического движения системы с
периодом
 .
Поэтому после каждого шага проверяется
условие
.
Поэтому после каждого шага проверяется
условие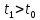 ,
гдеt
- текущее значение времени.
,
гдеt
- текущее значение времени.
Если
оно выполнено, то производится
интерполяционное уточнение состояния
в момент
 (с
помощью той же программыINTRP)
и сравниваются состояния при t=0
и
(с
помощью той же программыINTRP)
и сравниваются состояния при t=0
и
 С этой вычисляется величина:
С этой вычисляется величина:
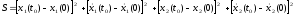 (30)
(30)
При
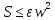 ,
где
,
где - заданное малое число,w
- максимальное значение модуля фазовых
координат за время интегрирования,
периодическое решение считается
достигнутым. В противном случае состояние
при
- заданное малое число,w
- максимальное значение модуля фазовых
координат за время интегрирования,
периодическое решение считается
достигнутым. В противном случае состояние
при
 принимается
в качестве начального и процесс
повторяется.
принимается
в качестве начального и процесс
повторяется.
При
достижении периодического решения
полученные значения перемещений и
скоростей на протяжении цикла переводятся
в различные величины (м, м/с) и выводятся
на печать вместе со значением времени
(фазовых углов wt).
В той же таблице приводятся относительное
перемещение двух масс, кроме этого
приводятся моменты перехода от раздельного
движения к совместному ( )
и обратно (
)
и обратно ( );
мощность, затрачиваемая на колебания
при периодическом движении.
);
мощность, затрачиваемая на колебания
при периодическом движении.
Периодическое
решение определяется с заданной точностью
 .
В некоторых случаях (если абсолютное
значение
.
В некоторых случаях (если абсолютное
значение
 велико) принятой точности может оказаться
недостаточно. Тогда следует уменьшить
велико) принятой точности может оказаться
недостаточно. Тогда следует уменьшить (рекомендуемые значения
(рекомендуемые значения ).
С другой стороны, уменьшение
).
С другой стороны, уменьшение приводит к росту числа цикла, необходимого
для установления периодического решения,
то есть к увеличению продолжительности
интегрирования. Рекомендуется при
проведении расчетов эмпирическим путем
подобрать наиболее подходящее значение
приводит к росту числа цикла, необходимого
для установления периодического решения,
то есть к увеличению продолжительности
интегрирования. Рекомендуется при
проведении расчетов эмпирическим путем
подобрать наиболее подходящее значение
При заданной частоте удара и массе рабочего органа эффективность ударно-вибрационной машины определяется ударной скоростью [17]. Поскольку машина является резонансной, максимальная (резонансная) ударная скорость достигается лишь при конкретных значениях основных параметров.
Для
исследования расчетной модели при
 в соответствии с [8]. Относительная
ударная скорость будет иметь вид:
в соответствии с [8]. Относительная
ударная скорость будет иметь вид:

Отсюда
видно, что относительная ударная скорость
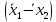 имеет максимальное значение при
имеет максимальное значение при то есть
то есть Ф – фаза относительной ударной скорости.
Ф – фаза относительной ударной скорости.

где
R
– коэффициент восстановления скорости

a, b- коэффициенты, определяющиеся из исходных данных параметров системы;
 максимальная
относительная ударная скорость. Эта
скорость достигается при оптимальной
фазе вынуждающей силы
максимальная
относительная ударная скорость. Эта
скорость достигается при оптимальной
фазе вынуждающей силы
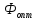

Из
выражения (25) следует, что для режимов
с максимальной относительной ударной
скоростью, фаза равна
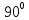 или фаза вынуждающей силы в момент удара
равна
или фаза вынуждающей силы в момент удара
равна .
Причем независимо от значения параметров,
при которых достигнут максимум
относительной ударной скорости и от
величины этого максимума.
.
Причем независимо от значения параметров,
при которых достигнут максимум
относительной ударной скорости и от
величины этого максимума.
Данный
результат получен для идеализированной
системы
 ,
чего в действительности не может быть.
,
чего в действительности не может быть.
При
 ,
то есть для линейной системы, результаты
исследований изложены в работах [5],
[17]. Фаза вынуждающей силы в момент удара
равна
,
то есть для линейной системы, результаты
исследований изложены в работах [5],
[17]. Фаза вынуждающей силы в момент удара
равна .
В линейной системе за момент удара
условно принимают момент перехода
системы через положение равновесия.
.
В линейной системе за момент удара
условно принимают момент перехода
системы через положение равновесия.
Таким
образом, при изменении
 от 0 до
от 0 до в
системах с одной степенью свободы
значения фазы вынуждающей силы изменяются
от
в
системах с одной степенью свободы
значения фазы вынуждающей силы изменяются
от
Для
систем с двумя степенями свободы
обозначим
 -
фазовый угол, соответствующий фазовому
углу ударной скорости в момент
сопротивления
-
фазовый угол, соответствующий фазовому
углу ударной скорости в момент
сопротивления
 фазовый угол в момент отрыва
фазовый угол в момент отрыва фазовый угол в момент перехода скорости
через нуль. Согласно принятому отчету
при
фазовый угол в момент перехода скорости
через нуль. Согласно принятому отчету
при

Для двухмассной ударно-вибрационной установки с эксцентриково-шатунным приводом применим следующие рассуждения.
В следующем блоке осуществляется преобразования, необходимые для приведения уравнений к единому виду. Вводятся безразмерные переменные – время и перемещение. Далее задаются стандартные начальные условия, соответствующие наличию положительного расстояния между массами m1 и m2 и параметры, необходимые для начала интегрирования.
Тип движения определяется знаком относительного перемещения:
 . (34)
. (34)
