МАТЕМАТИКА (ІДЗ) / Rozdil1_10

10. ВЛАСНІ ВЕКТОРИ І ВЛАСНІ ЗНАЧЕННЯ.

ЗВЕДЕННЯ РІВНЯННЯ КРИВОЇ ДРУГОГО ПОРЯДКУ

ДО КАНОНІЧНОГО ВИГЛЯДУ

1. Власні вектори і власні значення. Число називається власним числом лінійного оператора а ненульовий вектор власним вектором цього оператора, що відповідає власному числу якщо число і вектор такі, що = . В кінцевовимірному лінійному просторі дана рівність еквівалентна матричній

. (1.32)

Звідси випливає, що число є власне число оператора тоді і тільки тоді, коли

(1.33)

Рівняння (1.33) називається характеристичним рівнянням, дематриця лінійного оператора в прямокутному базисі.

Якщо , а то власні числа (значення) знаходяться із рівняння (1.33)

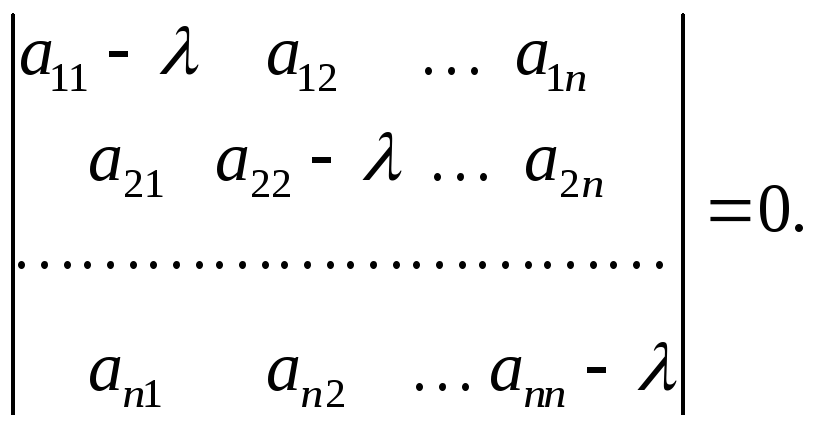
Координати власних векторів, що відповідають власним значеннямвизначаються як ненульові розв’язки однорідної системи рівнянь

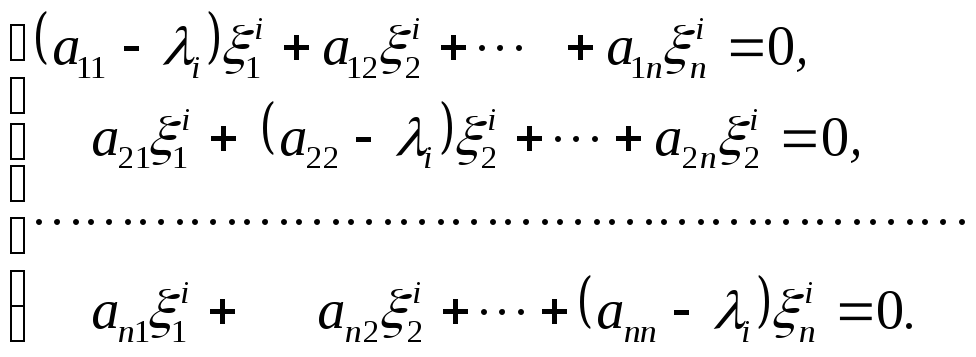
2. Зведення рівняння кривої другого порядку до канонічного вигляду. Загальне рівняння кривої другого порядку на площині

(1.34)

Матриця квадратичної форми лівої частини рівняння має такий вигляд

Із характеристичного рівняння 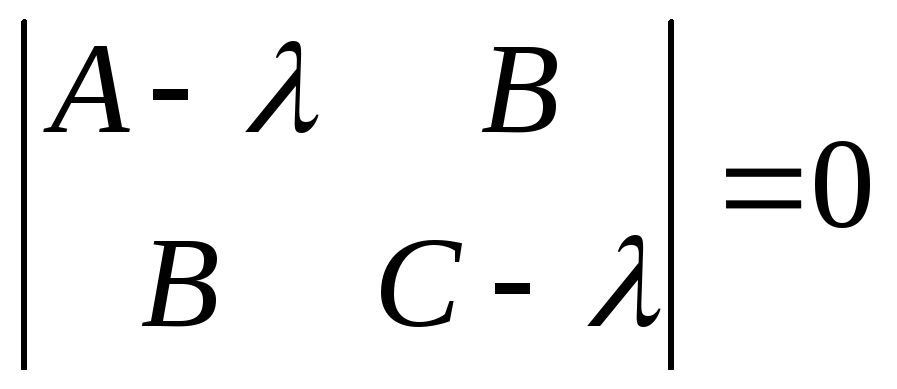знаходимо

власні числа і а із системи рівнянь

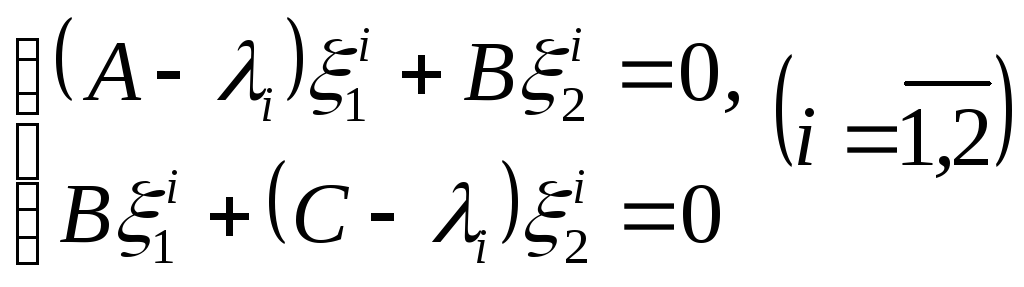
знаходимо ненульові розв’язки, які дадуть два власних вектори

і матриці квадратичної форми. Пронормувавши вектори знайдемо їх напрямні косинуси

З допомогою перетворення

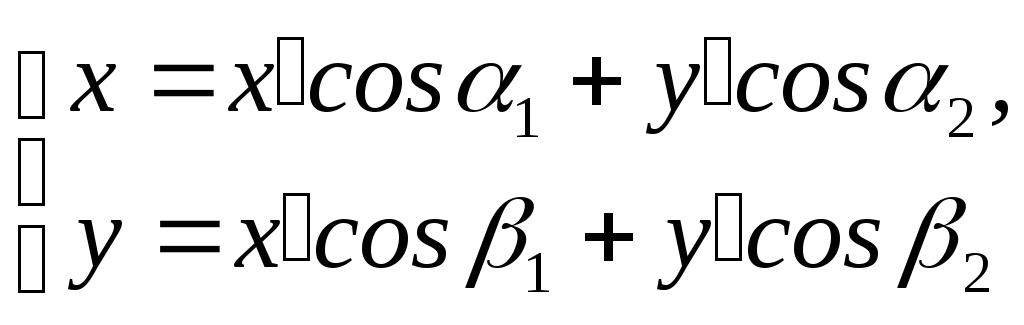
квадратична форма зводиться до канонічного вигляду

,

а рівняння кривої другого порядку (1.34) в системі координат

(в базисі із власних векторів) приймає такий вигляд

(1.35)

З допомогою паралельного переносу системи координат рівняння кривої (1.35) зводиться до канонічного виляду.

АР-1.10

1. Знайти власні значення і власні вектори лінійних операторів, заданих своїми матрицями:

а) б)

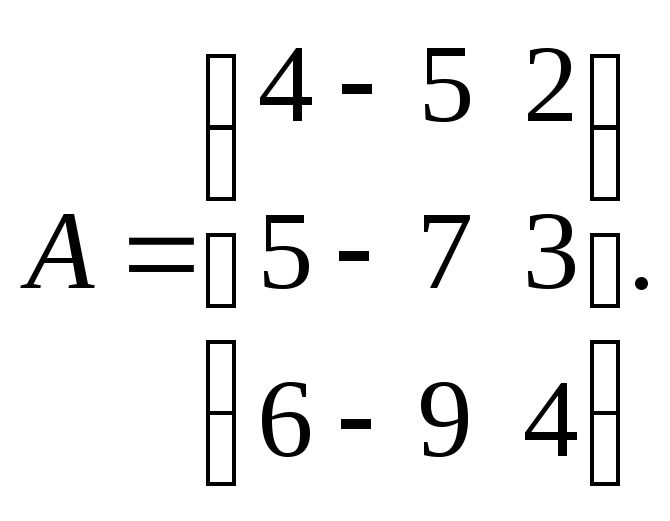
2. Написати канонічне рівняння кривої другого порядку, визначити тип і побудувати її:

а)

б)

(Відповідь: а) гіпербола б) паралельні прямі ).

СР-1.10

1. Знайти ортогональне перетворення, що приводить квадратичну форму до канонічного вигляду, і написати цей канонічний вигляд

(Відповідь: ).

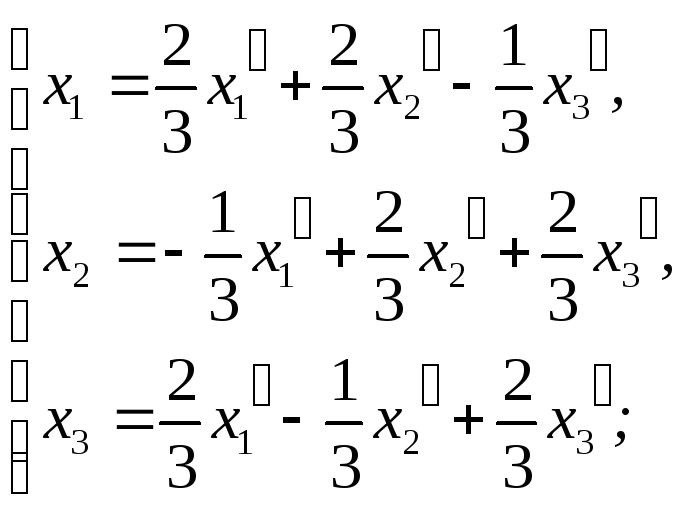
2. Написати канонічне рівняння кривої другого порядку, визначити тип і побудувати її:

(Відпровідь: парабола

ІДЗ-1.10

1. Знайти власні значення та власні вектори матриці

1.1. 1.2. 1.3.

1.4. 1.5. 1.6.

1.7. 1.8. 1.9.

1.10. 1.11. 1.12.

1.13. 1.14. 1.15.

1.16. 1.17. 1.18.

1.19. 1.20. 1.21.

1.22. 1.23. 1.24.

1.25. 1.26. 1.27.

1.28. 1.29. 1.30.

2. Звести до канонічного вигляду рівняння кривої другого порядку, використовуючи теорію квадратичних форм. Побудувати стару та нову системи координат і криву (якщо вона існує).

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

19. 

20. 

21. 

22. 

23. 

24. 

25. 

26. 

27. 

28. 

29. 

30. 

РОЗВ’ЯЗОК ТИПОВОГО ВАРІАНТА

1. Знайти власні значення та власні вектори матриці

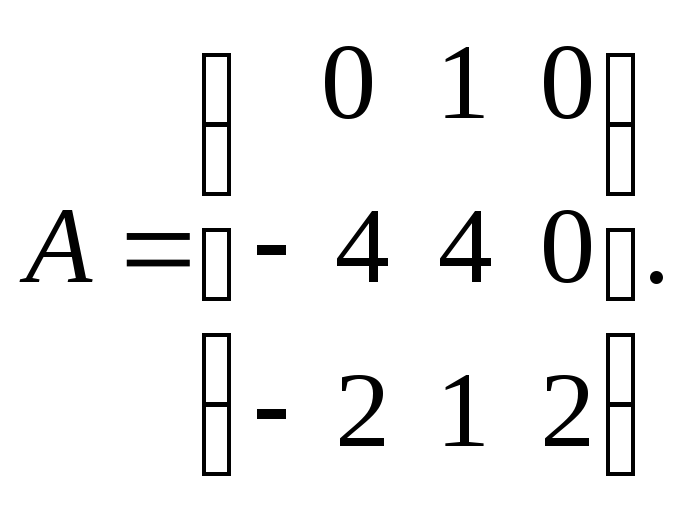
Запишемо характеристичне рівняння (1.33)

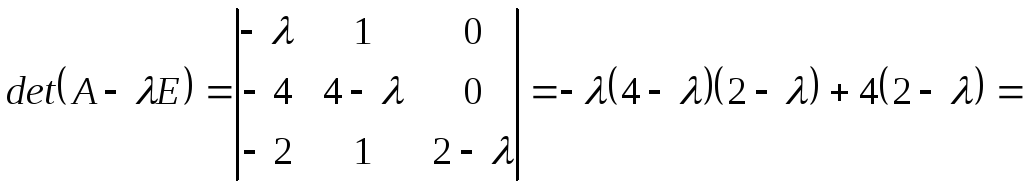
, тоді і власні значення матриці Нехай власний вектор, що відповідає власному значенню Для визначення його координат запишемо систему рівнянь

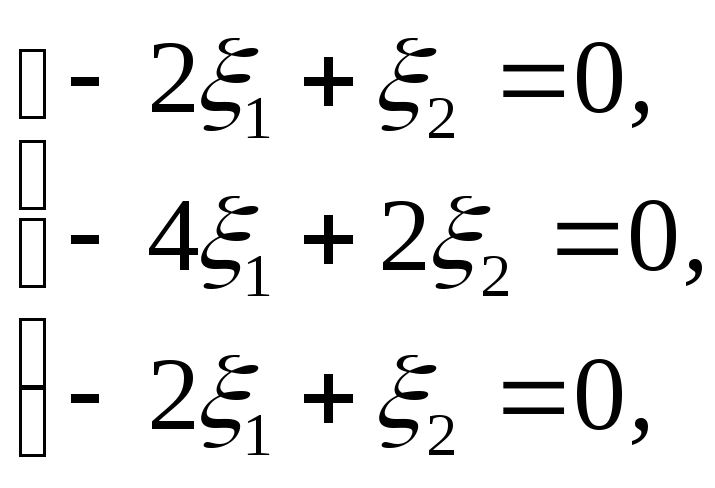загальний розв’язок якої буде

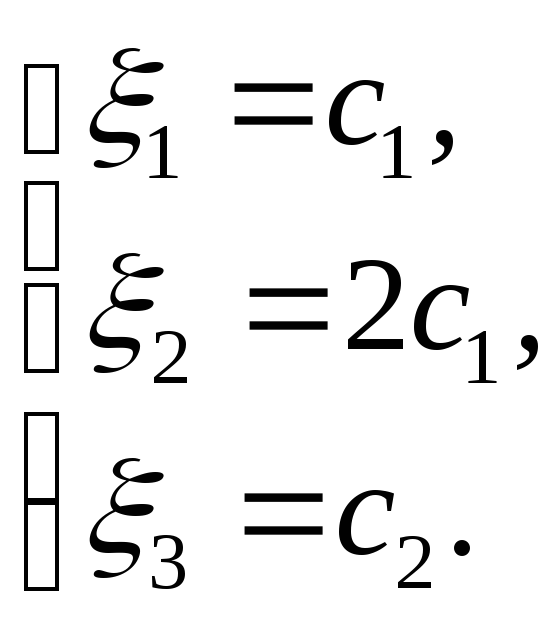
Оскільки ми шукаємо ненульові розв’язки однорідної системи, то, покладаючи і одержимо два

власних вектори, що відповідають власному значенню

і причому

2. Звести до канонічного вигляду рівняння кривої другого порядку, використовуючи теорію квадратичних форм. Побудувати стару та нову системи координат і криву.

Матриця квадратичної форми має такий вигляд . Знайдемо її власні значення та власні вектори:

Нехай власний вектор, що відповідає власному значенню Тоді для знаходження його координат одержимо

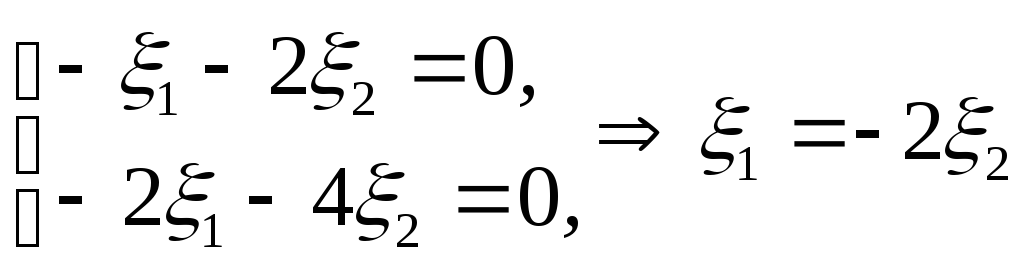, наприклад, і

Аналогічно, нехай власний вектор, що відповідає власному значенню тоді

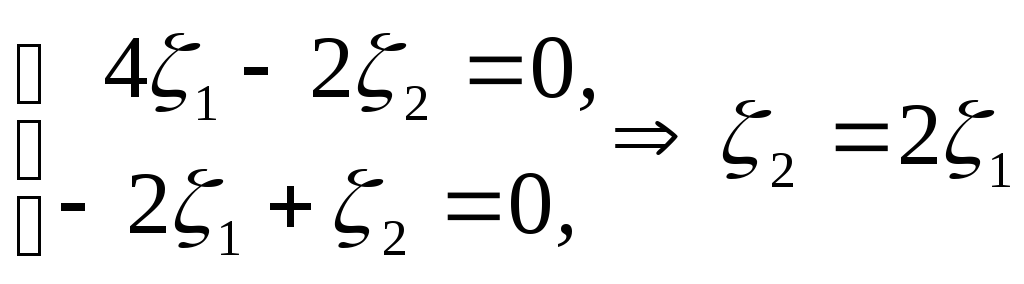і , наприклад, тоді

Очевидно, що ().

Квадратична форма приймає канонічний вигляд а рівняння кривої зводиться до канонічного

або (еліпс). Вісь співпадає з власним вектором а вісь з власним вектором

Перетворення, що приводить квадратичну форму до канонічного вигляду

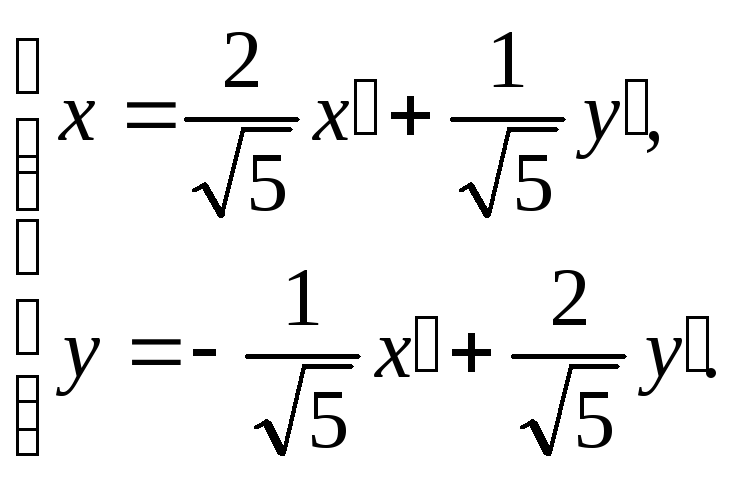
В системі координат будуємо дану криву (рис.1.12).

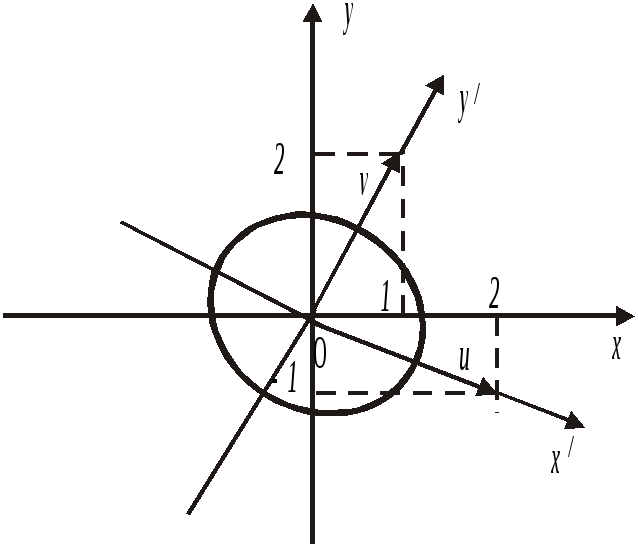
Рис.1.12

99