
МАТЕМАТИКА (ІДЗ) / Rozdil1_13
.doc-
НЕПЕРЕРВНІСТЬ ФУНКЦІЇ.
КЛАСИФІКАЦІЯ ТОЧОК РОЗРИВУ
Функція
![]() із областю визначення
із областю визначення
![]() називається неперервною в точці
називається неперервною в точці
![]() якщо
якщо![]() Ця умова еквівалентна таким:
Ця умова еквівалентна таким:
-
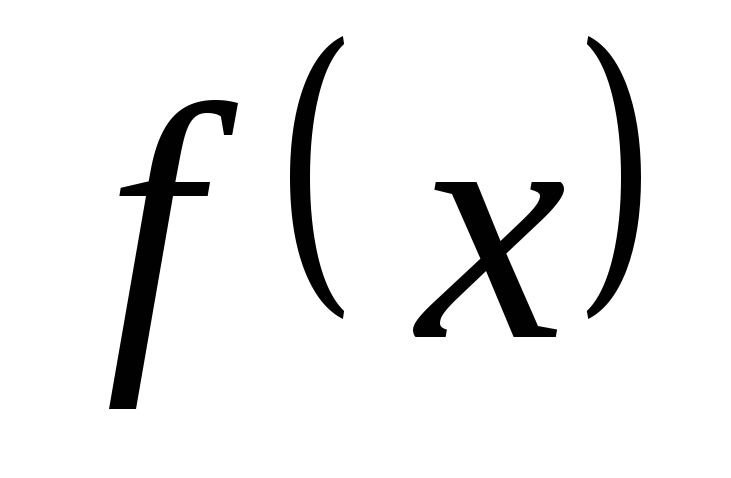 визначена
в точці
визначена
в точці
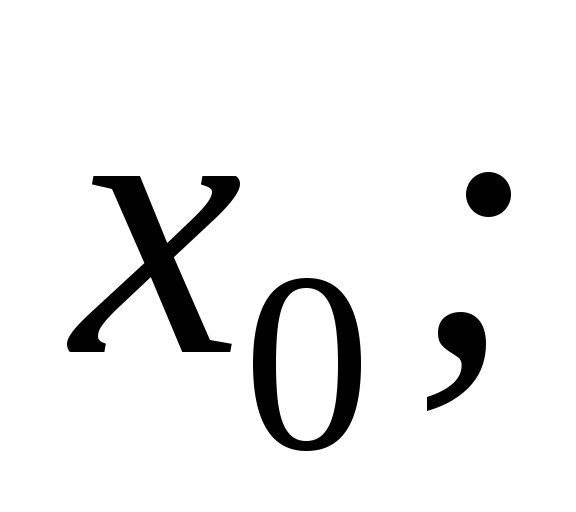
-
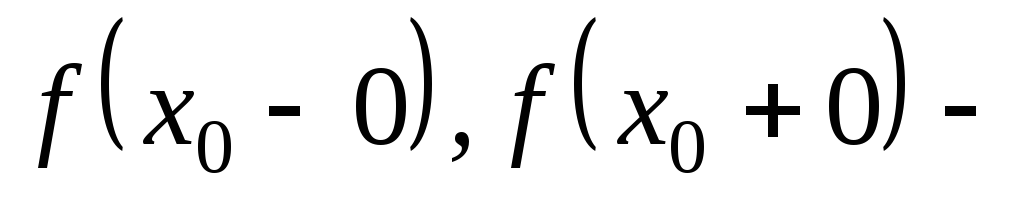 існують
і скінченні;
існують
і скінченні; -
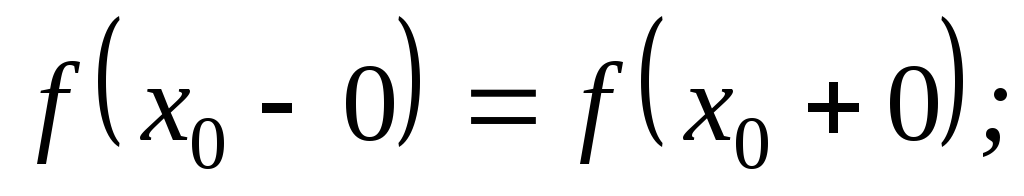
-

Якщо
хоча б одна із цих чотирьох умов не
виконується, то
функція
![]() терпить в точці
терпить в точці
![]() розрив. В залежності від того, які саме
умови не виконуються, розриви класифікуються
як розриви 1-го роду (усувні
та розриви типу «стрибка»)
і розриви 2-го роду (безмежні
та істотні).
розрив. В залежності від того, які саме
умови не виконуються, розриви класифікуються
як розриви 1-го роду (усувні
та розриви типу «стрибка»)
і розриви 2-го роду (безмежні
та істотні).
Функція
![]() називається неперервною на множині
називається неперервною на множині
![]() якщо вона непервна в кожній точці
якщо вона непервна в кожній точці
![]() Елементарні функції є неперервними на
своїй області визначення.
Елементарні функції є неперервними на
своїй області визначення.
АР-1.13
-
Знайти
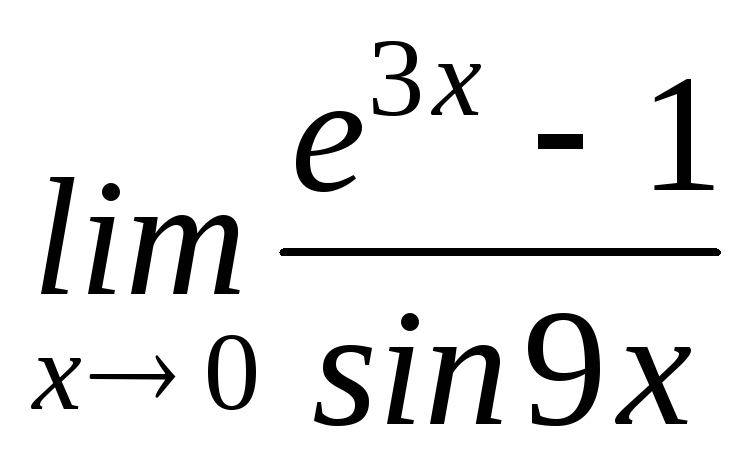 .
. -
Знайти
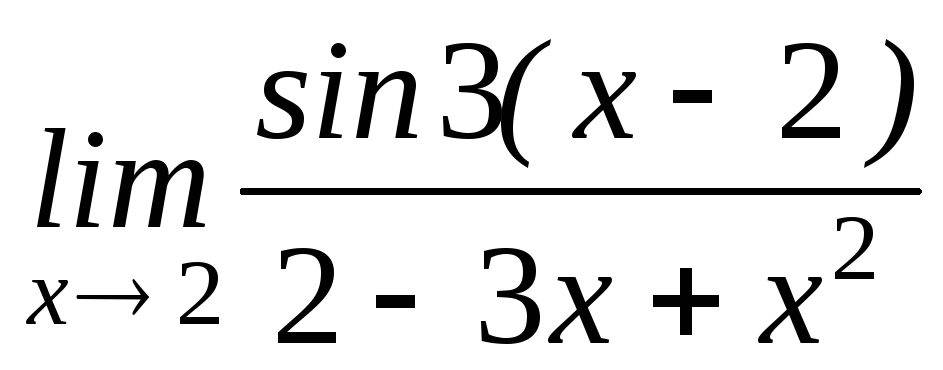 .
.
3.
Знайти
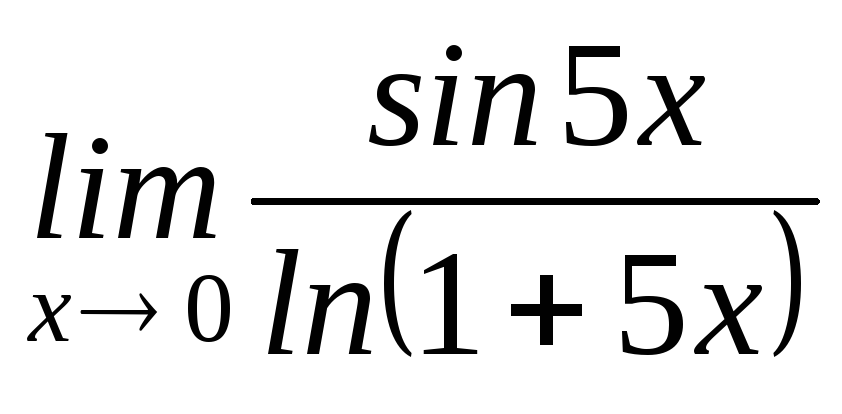 .
.
4. Визначити
порядок нескінченно малої функції
![]()
відносно
нескінченно малої
 при
при
 .
.
5.
Визначити
область
неперервності функції
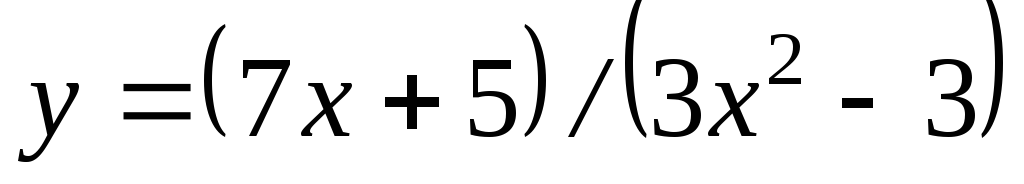 і знайти точки розриву.
і знайти точки розриву.
6. Дано функцію

Знайти точки розриву функції і побудувати її графік.
7. Дослідити
на неперервність функцію
![]() в
точках
в
точках
![]() і
і
![]() .
.
СР-1.13
-
1) Знайти
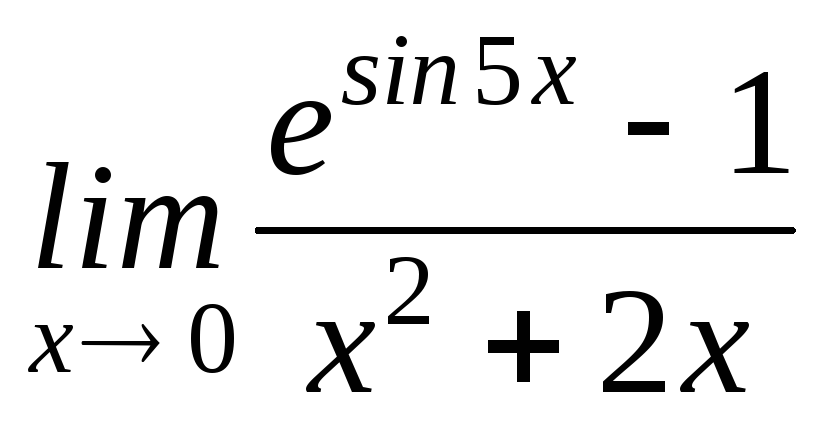 .
( Відповідь:
5/2).
.
( Відповідь:
5/2).
2) Дослідити
на неперервність функцію
![]() в
точках
в
точках
![]() Виконати
схематичне креслення.
Виконати
схематичне креслення.
-
1) Знайти
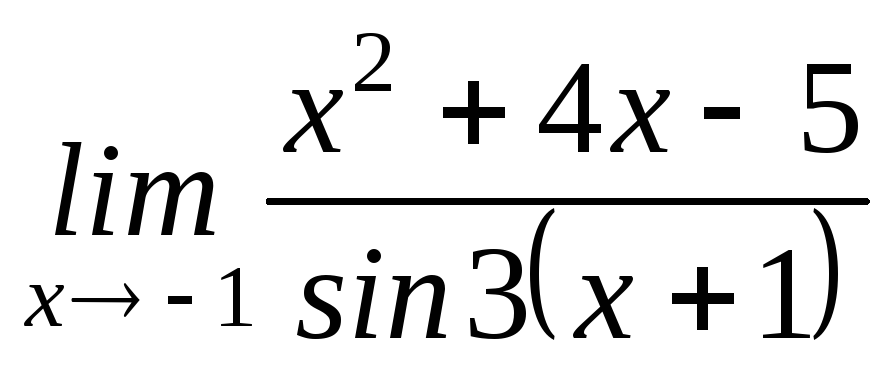 .
(Відповідь: -3/4).
.
(Відповідь: -3/4). -
Дано функцію

Дослідити її на неперервність. Виконати схематичне креслення.
-
1) Знайти
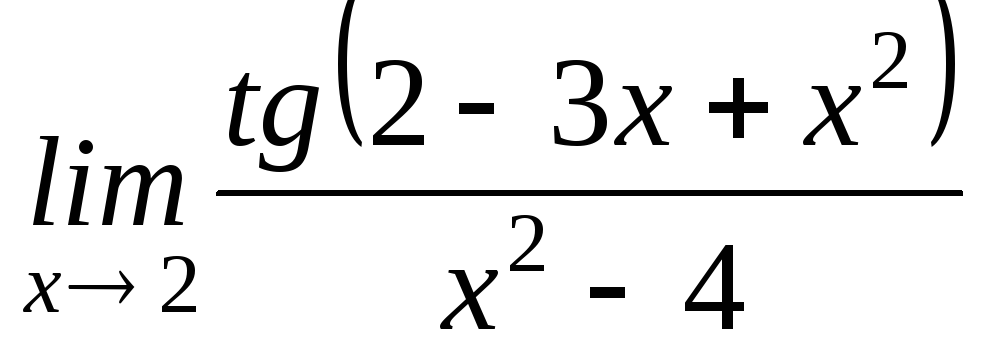 .
(Відповідь:
1/4).
.
(Відповідь:
1/4). -
Дослідити на неперервність функцію
![]() в
точках
в
точках
![]() і
і
![]() Виконати схематичне
креслення.
Виконати схематичне
креслення.
ІДЗ-1.13
1. Довести,
що функції
![]() і
і
![]() при
при
![]() є
нескінченно малими одного порядку
малості.
є
нескінченно малими одного порядку
малості.
1.1.
![]() .
.
1.2.
![]() .
.
1.3.
![]() .
.
1.4.
![]() .
.
1.5.
![]() .
.
1.6.
![]()
1.7.
![]() .
.
1.8.
![]()
1.9.
![]()
1.10.![]() .
.
1.11.![]() .
.
1.12.![]() 1.13.
1.13.![]() .
1.14.
.
1.14.![]() 1.15.
1.15.![]() .
1.16.
.
1.16.![]()
1.17.![]()
1.18.![]() .
.
1.19.![]() .
.
1.20.![]() .
.
1.21.![]() .
.
1.22.![]() .
.
1.23.![]() .
.
1.24.![]() .
.
1.25.![]() .
.
1.26.![]() .
.
1.27.![]() .
.
1.28.![]() .
.
1.29.![]() .
.
1.30.![]() .
.
2. Знайти границі, використовуючи еквівалентні нескінченно малі функції.
2.1.
![]() .
2.2.
.
2.2.
![]() .
.
2.3.
![]() .
2.4.
.
2.4.
![]()
2.5.
![]() .
2.6.
.
2.6.
![]() .
.
2.7.
![]() .
2.8.
.
2.8.
![]() .
.
2.9.
![]() .
2.10.
.
2.10.![]() .
.
2.11.![]() .
2.12.
.
2.12.![]() .
.
2.13.![]() . 2.14.
. 2.14.![]() .
.
2.15.![]() .
2.16.
.
2.16.
![]() .
.
2.17.![]() .
2.18.
.
2.18.
![]() .
.
2.19.![]() .
2.20.
.
2.20.![]() .
.
2.21.![]() .
2.22.
.
2.22.![]() .
.
2.23.![]() .
2.24.
.
2.24.
![]() .
.
2.25.![]() .
2.26.
.
2.26.![]() .
.
2.27.
![]() .
2.28.
.
2.28.![]() .
.
2.29.
![]() .
2.30.
.
2.30.
![]()
3. Дослідити дані функції на неперервність та побудувати їх графіки.
3.1.
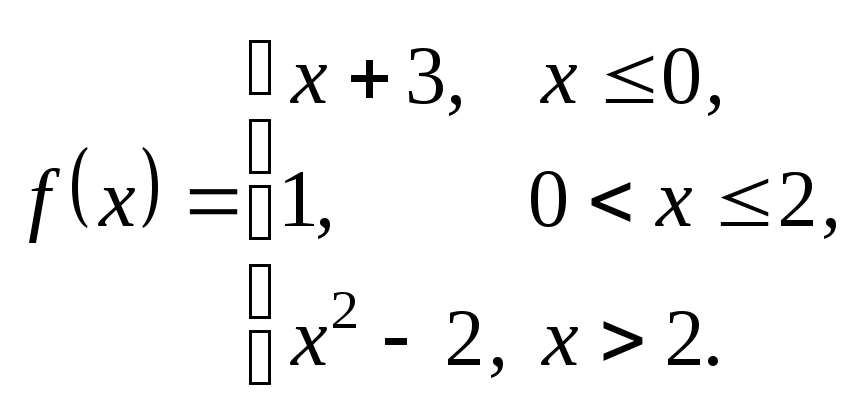 3.2.
3.2.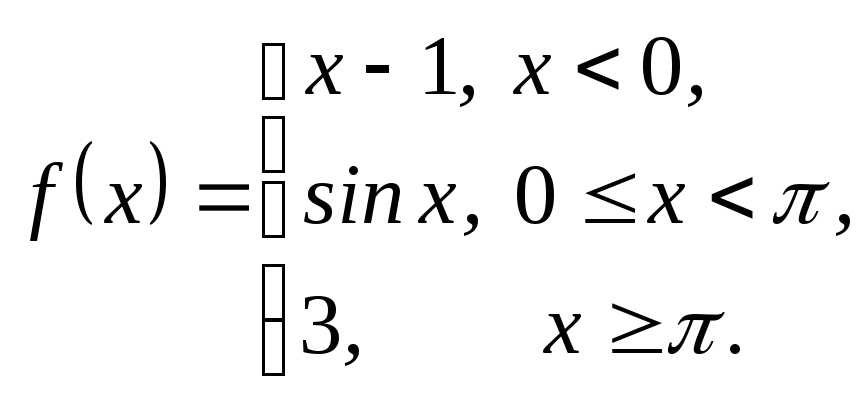
3.3.
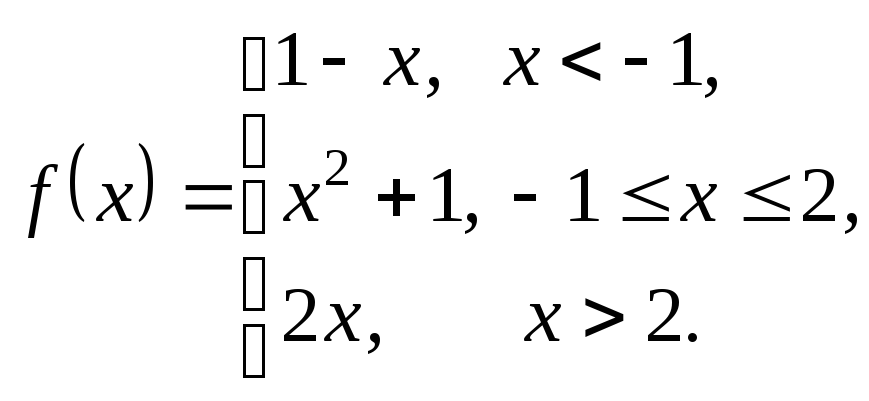 3.4.
3.4.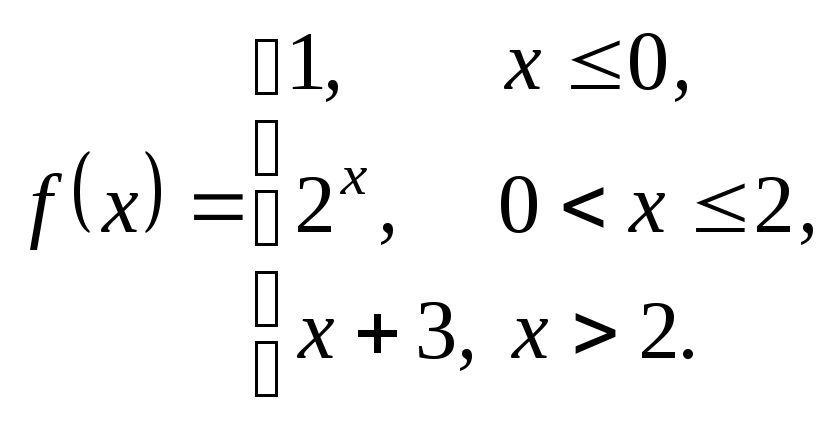
3.5.
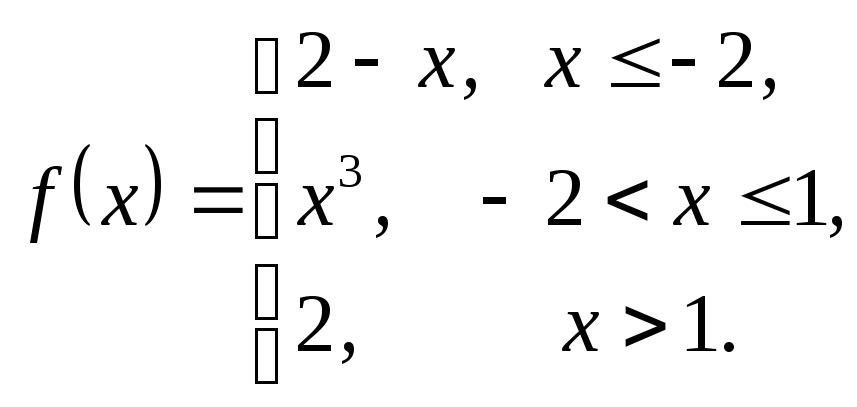 3.6.
3.6.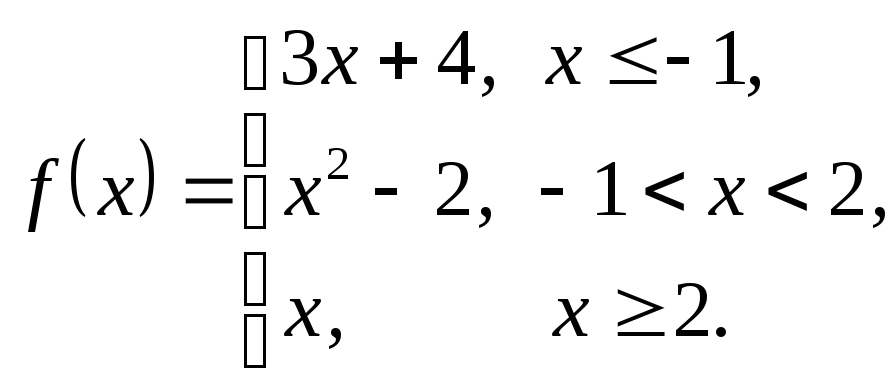
3.7.
 3.8.
3.8.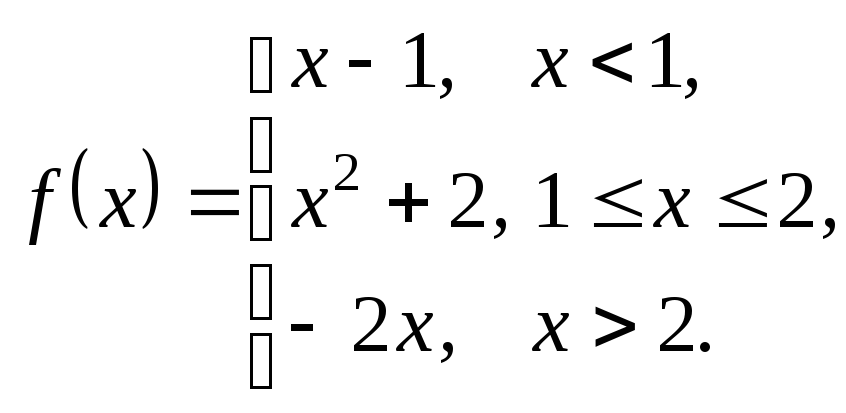
3.9.
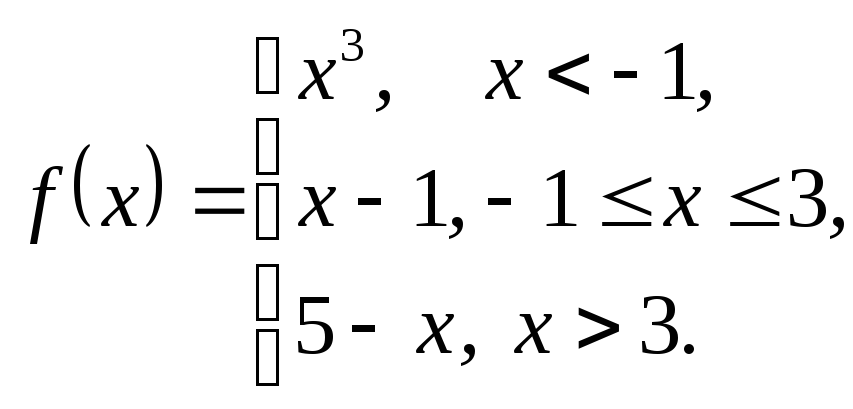 3.10.
3.10.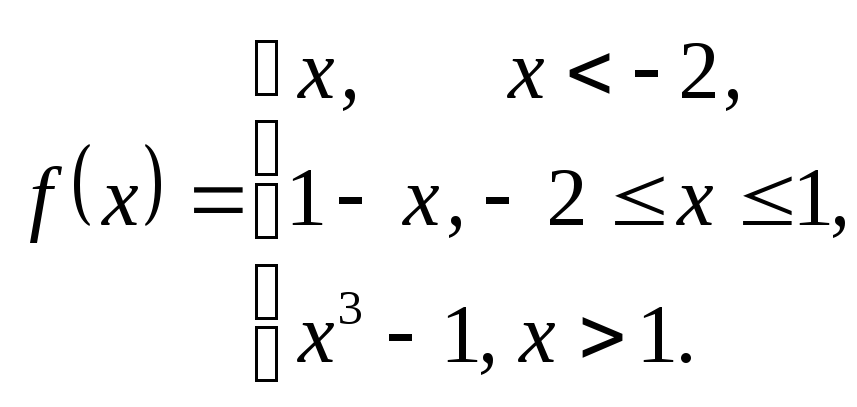
3.11. 3.12.
3.12.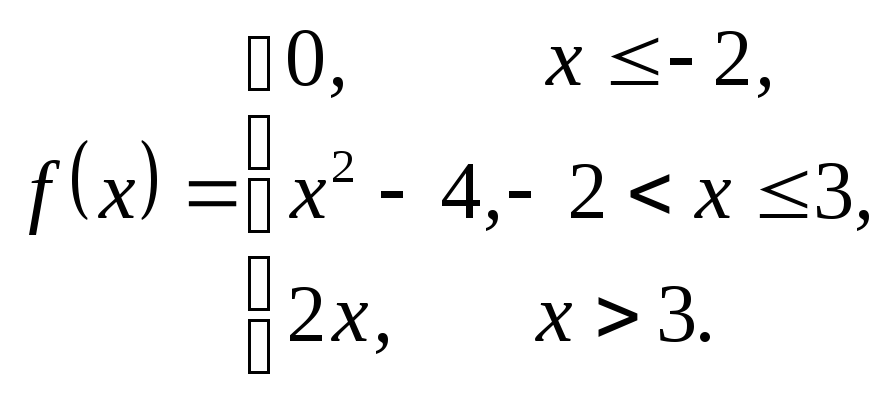
3.13.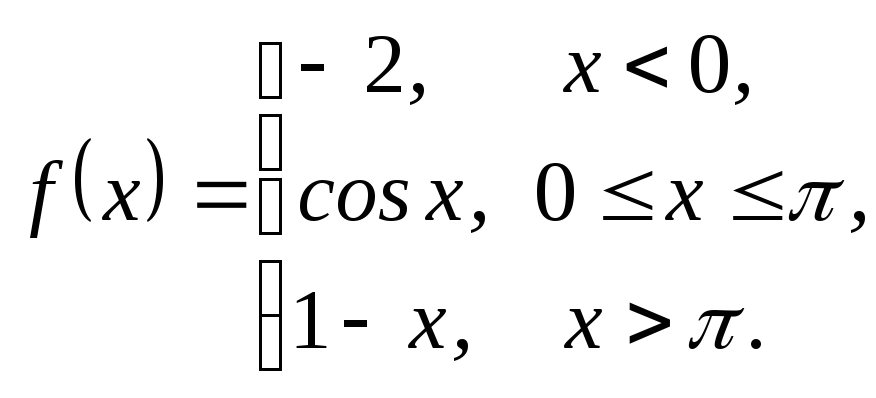 3.14.
3.14.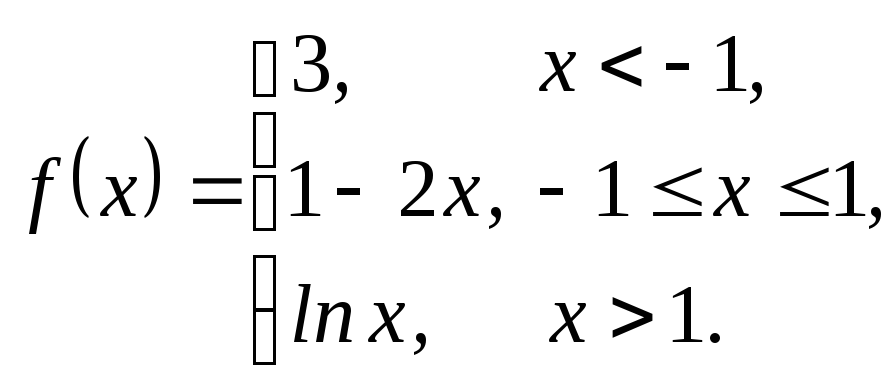
3.15.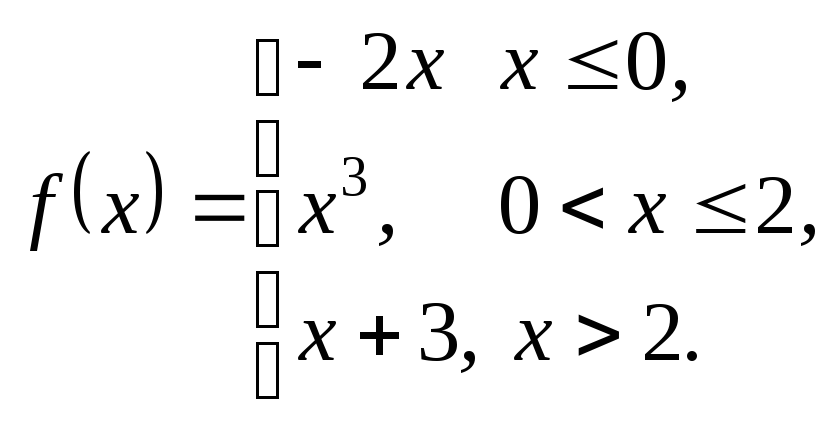 3.16.
3.16.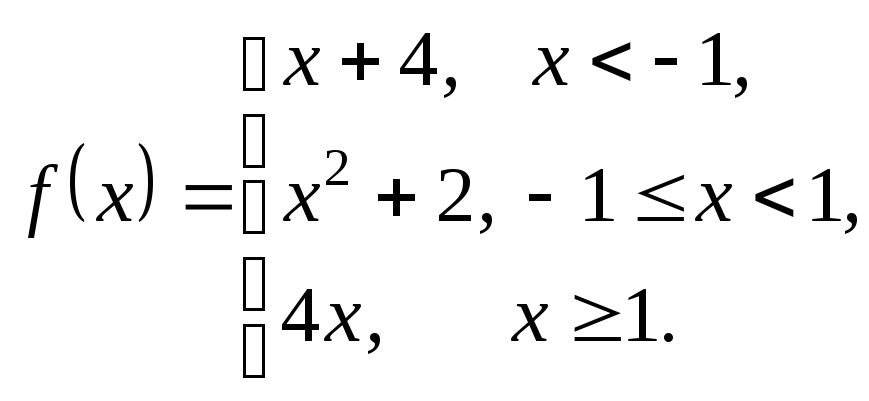
3.17.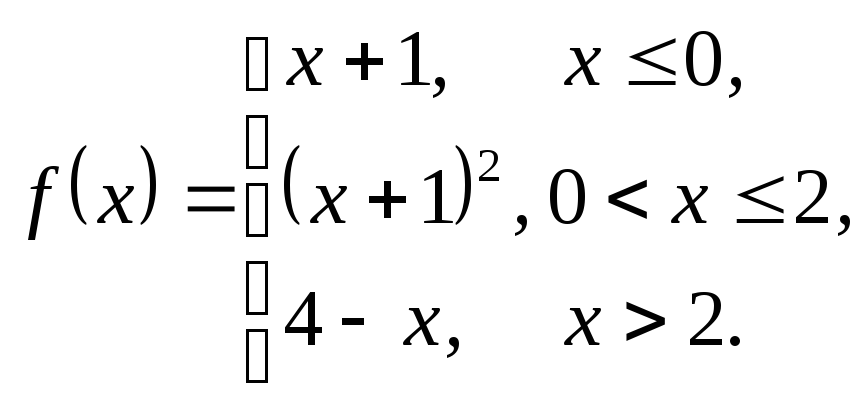 3.18.
3.18.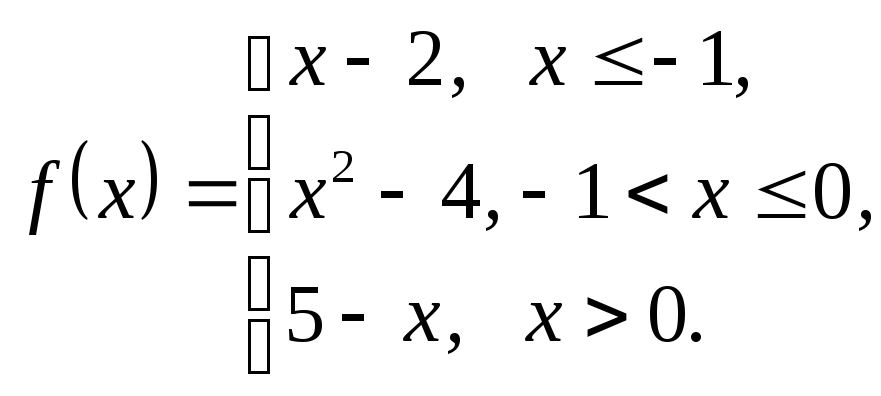
3.19.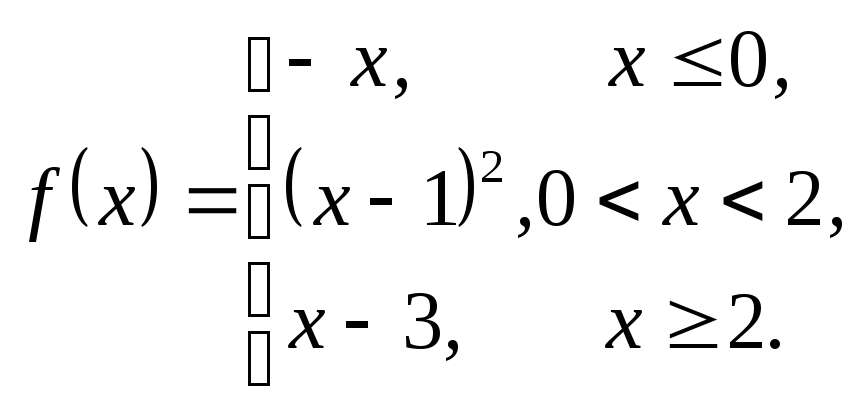 3.20.
3.20.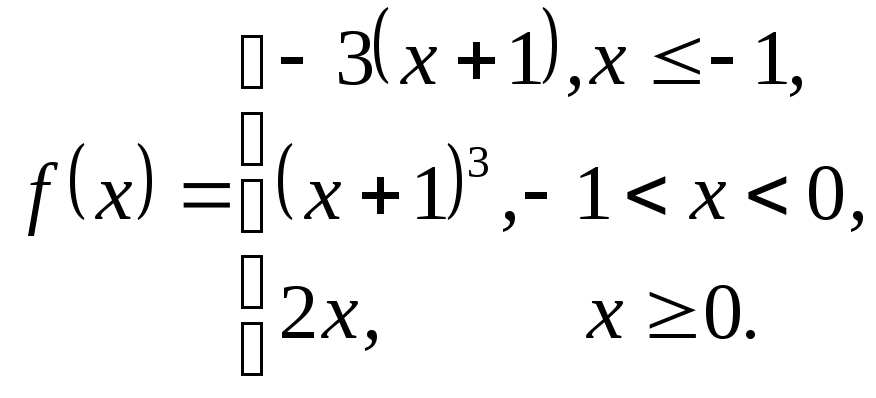
3.21.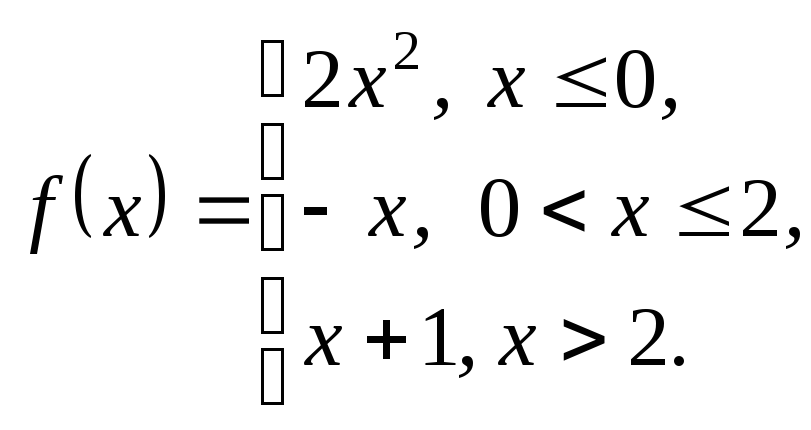 3.22.
3.22.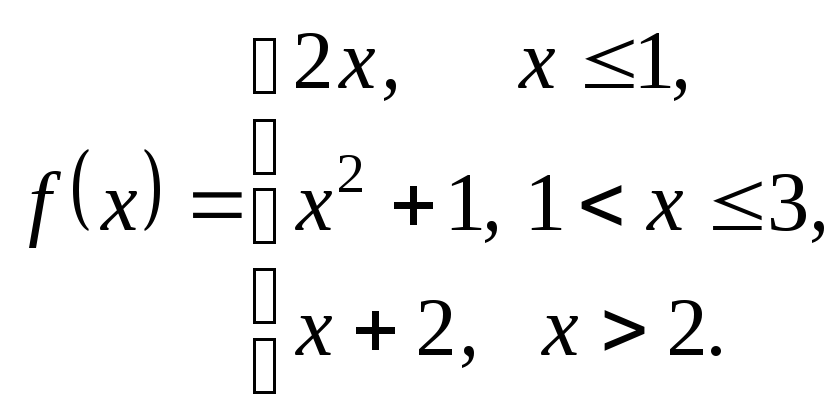
3.23. 3.24.
3.24.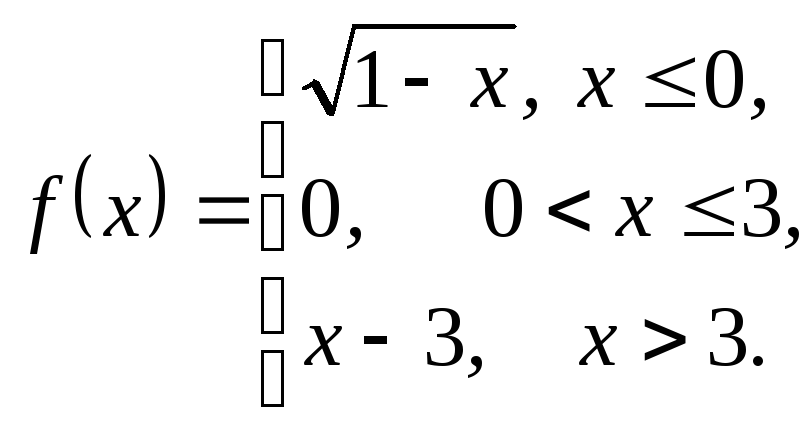
3.25.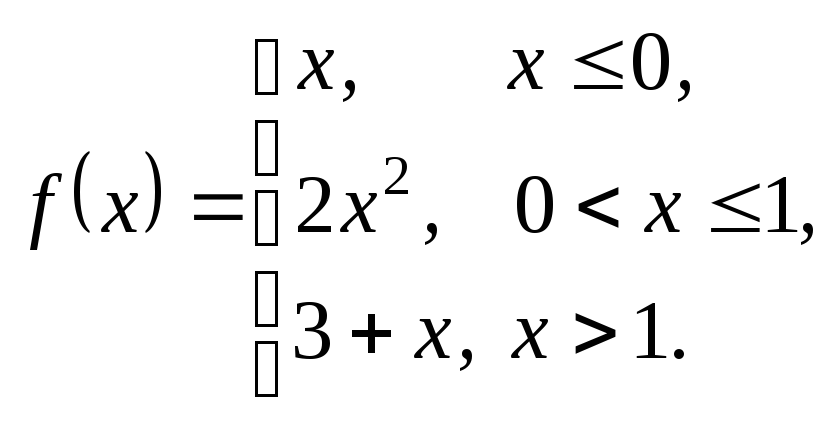 3.26.
3.26.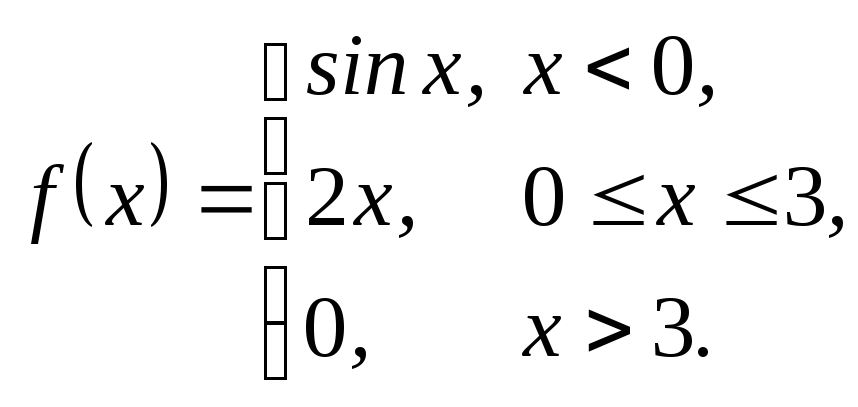
3.27.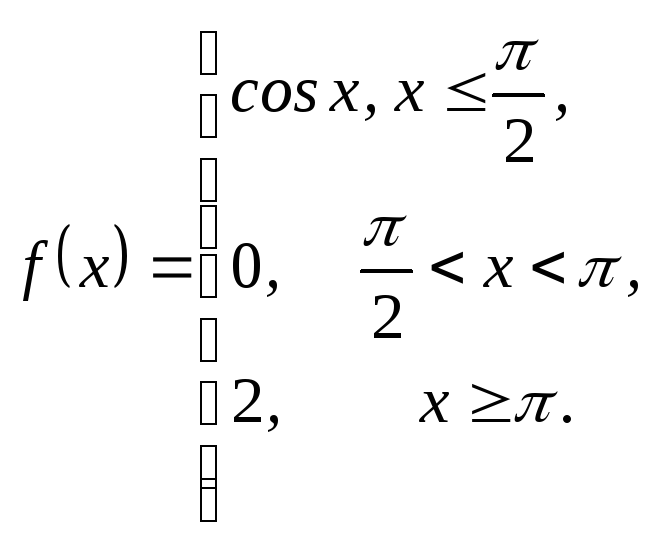 3.28.
3.28.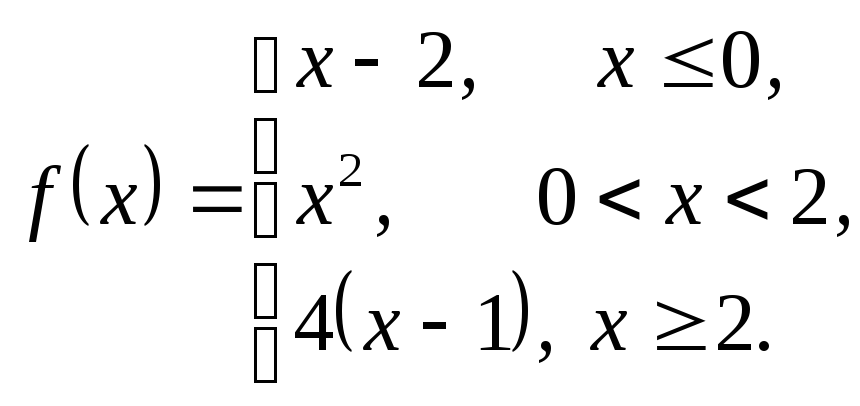
3.29.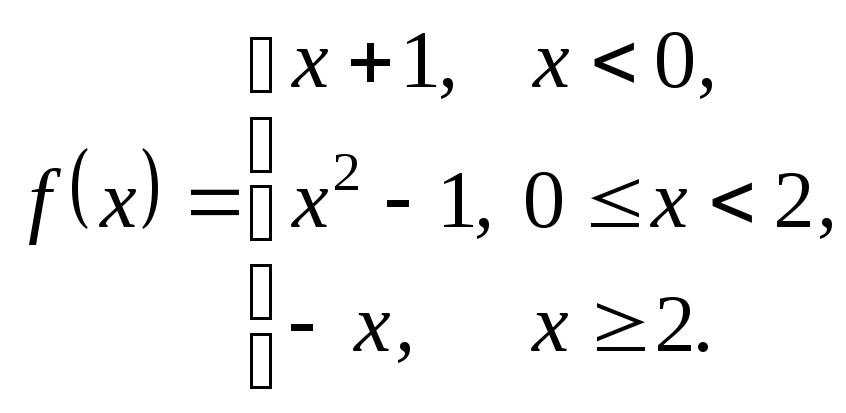 3.30.
3.30.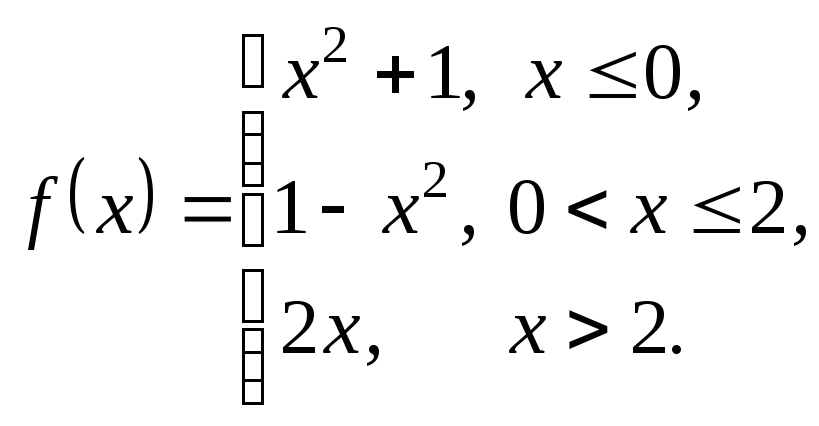
4. Дослідити дані функції на неперервність у вказаних точках.
4.1.
![]()
4.2.
![]()
4.3.
![]()
4.4.
![]()
4.5.
![]()
4.6.
![]()
4.7.
![]()
4.8.
![]()
4.9.
![]()
4.10.
![]()
4.11.
![]()
4.12.
![]()
4.13.
![]()
4.14.
![]()
4.15.
![]()
4.16.
![]()
4.17.
![]()
4.18.
![]()
4.19.
![]()
4.20.
![]()
4.21.
![]()
4.22.
![]()
4.23.
![]()
4.24.
![]()
4.25.
![]()
4.26.
![]()
4.27.
![]()
4.28.
![]()
4.29.
![]()
4.30.
![]()
РОЗВ’ЯЗОК ТИПОВОГО ВАРІАНТА
1.
Довести, що функції
![]() і
і
![]() є нескінченно малими одного порядку
малості.
є нескінченно малими одного порядку
малості.
Знаходимо
![]()
![]()
Оскільки
границя відношення функцій
![]() дорівнює відмінній від нуля сталій, то
у відповідності з означенням дані
функції - нескінченно малі одного порядку
малості.
дорівнює відмінній від нуля сталій, то
у відповідності з означенням дані
функції - нескінченно малі одного порядку
малості.
2. Знайти границю, використовуючи еквівалентні нескінченно малі функції.
Маємо:![]()
3.Дослідити дану функцію на неперервність і побудувати її графік:
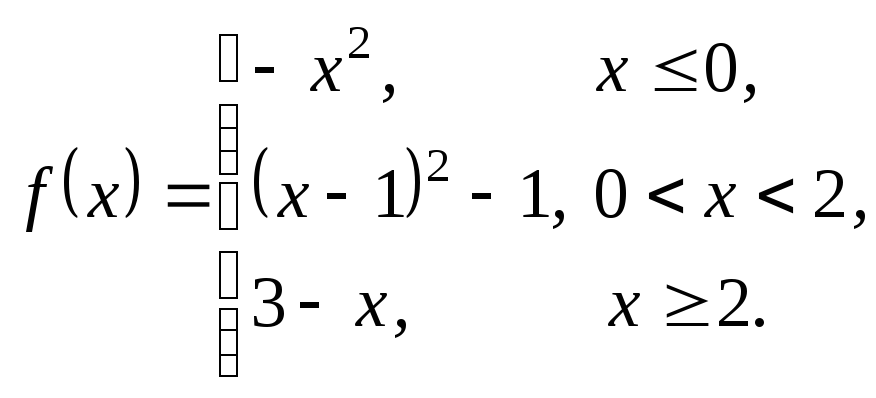
Функція
![]() визначена і неперервна на інтервалах
визначена і неперервна на інтервалах
![]() ,
,
![]() і
і
![]() ,
де вона задана елементарними функціями.
Отже, розрив може бути тільки в точках
,
де вона задана елементарними функціями.
Отже, розрив може бути тільки в точках
![]()
-
Для точки
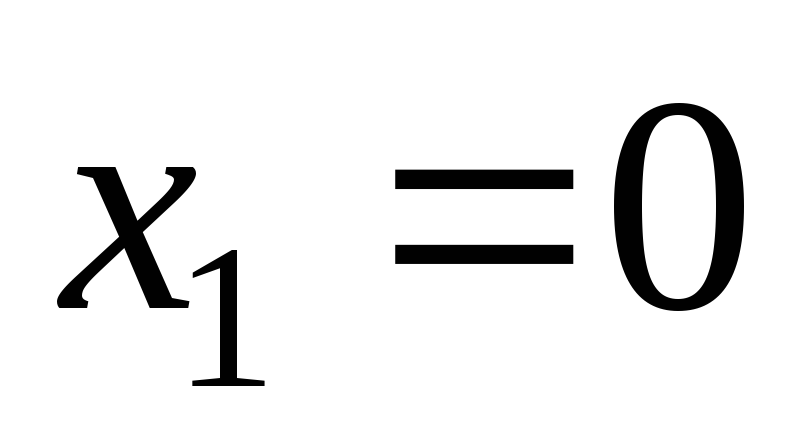 маємо:
маємо:
![]() ,
,
![]() тобто,
функція
тобто,
функція
![]() в точці
в точці
![]() неперервна.
неперервна.
2)Для
точки
![]() знаходимо:
знаходимо:
![]()
![]() тобто,
в точці
тобто,
в точці
![]() функція має розрив
функція має розрив
першого
роду;
виконує «стрибок»,
що дорівнює
![]()
Графік даної функції зображено на рис1.16.
4. Дослідити функцію
![]() на неперервність в точках
на неперервність в точках
![]()
Для точки
![]() маємо:
маємо:
![]()
![]()
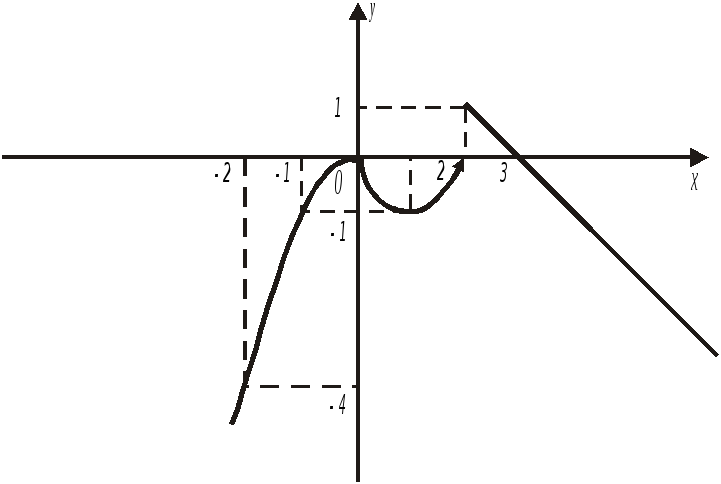
Рис.1.16
тобто, в точці
![]() функція
функція
![]() має нескінченний розрив другого роду.
має нескінченний розрив другого роду.
Для точки
![]() маємо:
маємо:
![]()
![]()
![]()
Отже, в точці
![]() функція
функція
![]() неперервна.
неперервна.
