
Mathcad - ЛР2
.pdf
Введем функцию определения диагонального преобладания:
check_diag_dom(A) := |
m ¬ rows(A) |
|
|
|||
|
answer ¬ "Есть диагональное преобладание!" |
|
|
|||
|
for i Î 1 .. m |
|
|
|||
|
|
row_part_sum ¬ 0 |
|
|
||
|
|
|
|
|||
|
|
for j Î 1 .. m |
|
|
||
|
|
|
|
|
|
|
|
|
row_part_sum ¬ row_part_sum + |
Ai , j |
if |
i ¹ j |
|
|
|
|
|
|||
|
|
answer ¬ "Нет диагонального преобладания..." |
if row_part_sum ³ |
Ai , i |
||
|
answer |
|
|
|||
check_diag_dom(A) = "Есть диагональное преобладание!" - в данном случае итерационный
процесс сойдется к решению.
Введем функции преобразования исходной системы линейных уравнений к виду, пригодному для итераций
get_P(A) := |
m ¬ rows(A) |
get_G(A , B) := |
m ¬ rows(A) |
|||
|
for i Î 1 .. m |
|
for i Î 1 .. m |
|||
|
for j Î 1.. m |
|
Gi ¬ |
Bi |
|
|
|
Pi , j ¬ |
-Ai, j |
if (i ¹ j) |
Ai, i |
||
|
|
|||||
|
Ai , i |
G |
||||
|
P |
|
|
|
|
|
æ |
0 |
ç |
-0.4640625 |
ç |
|
ç |
-0.3413793103 |
P = ç |
0.5555555556 |
ç |
|
ç |
0.11 |
P := |
get_P(A) |
ç
è-0.4569230769
|
G := |
get_G(A , B) |
|
|
|
-0.1346801347 |
-0.101010101 |
0.6666666667 |
-0.0336700337 |
-0.0505050505 ö |
|
0 |
0 |
0.4640625 |
-0.03125 |
-0.03125 |
÷ |
÷ |
|||||
-0.4022988506 |
0 |
-0.2275862069 |
-0.0229885057 |
0 |
÷ |
0.1795735129 |
0.1346801347 |
0 |
0.0897867565 |
0.0336700337 |
÷ |
÷ |
|||||
-0.2777777778 |
-0.1222222222 |
0.44 |
0 |
-0.0444444444 |
÷ |
÷ |
|||||
-0.1076923077 |
-0.1846153846 |
0 |
-0.2461538462 |
0 |
ø |
æ |
1.92592592592593 |
ö |
ç |
-8.5546875 |
÷ |
ç |
÷ |
|
ç |
-0.533333333333333 |
÷ |
G = ç |
-2.29741863075196 |
÷ |
ç |
÷ |
|
ç |
-10.6511111111111 |
÷ |
ç |
÷ |
|
è |
2.07076923076923 |
ø |
Вводим функцию определения наименьшей из норм матрицы P:
min_norm (P) := |
s1 |
← Norm1(P) |
|
Norm1(P) = 1.92792044282346 |
|
s2 |
← Norm2(P) |
|
Norm2(P) = 1.49093514090293 |
|
s3 |
← NormInf(P) |
|
|
|
|
|
||
|
min_norm ← min(s) |
|
NormInf(P) = 0.995384615384615 |
|
|
number_of_min_norm ← 1 |
if |
min_norm = s1 |
|
|
number_of_min_norm ← 2 |
if |
min_norm = s2 |
|
|
number_of_min_norm ← 3 |
if |
min_norm = s3 |
|
|
S1 ← min_norm |
|
|
|
|
S2 ← number_of_min_norm |
|
|
|
|
S |
|
|
|
min_norm (P)1 = 0.995384615384615
min_norm (P)2 = 3
Минимальная из норм < 1 - достаточное
условие сходимости выполняется
Функция, возвращающая выбранную норму:
NormX(P , number_of_norm) := |
res_norm ← Norm1(P) |
if |
number_of_norm = 1 |
|
res_norm ← Norm2(P) |
if |
number_of_norm = 2 |
|
res_norm ← NormInf(P) |
if |
number_of_norm = 3 |
|
res_norm |
|
|
Реализуем функцию итерационного алгоритма нахождения корней системы линейных уравнений методом Якоби:
Jacobi(P , G , p, e) := |
|
min_n_P_val ¬ min_norm (P)1 |
|
|
|
||
|
|
min_n_P_num ¬ min_norm (P)2 |
|
|
|
||
|
|
return |
"Не выполняется достаточное условие сходимости!" if min_n_P_val ³ 1 |
||||
|
|
X1 ¬ G |
|
|
|
||
|
|
X2 ¬ P×X1 + G |
|
|
|
||
|
|
k ¬ 2 |
|
|
|
|
|
|
|
|
|
é |
|
(1 - min_n_P_val) ×e ù |
|
|
|
while |
êNormXëé(Xk - Xk−1), min_n_P_numûù |
³ |
|
ú |
|
|
|
||||||
|
|
|
|
ë |
|
min_n_P_val û |
|
|
|
|
k ¬ k + 1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Xk ¬ P×Xk−1 + G |
|
|
|
|
|
|
X |
if |
p = 0 |
|
|
|
|
|
k |
if |
p = 1 |
|
|
|
JacobiPlus(A , B , p , e) := |
|
if |
check_diag_dom(A) ¹ "Есть диагональное преобладание!" |
||||
|
|||||||
|
|
|
msg ¬ "В матрице A нет диагонального преобладания!" |
||||
|
|
|
|||||
|
|
|
return msg |
|
|
|
|
|
|
P ¬ get_P(A) |
|
|
|
||
|
|
G ¬ get_G(A , B) |
|
|
|
||
|
|
Jacobi(P , G , p , e) |
|
|
|
||
X := JacobiPlus(A , B , 0 , e)
k := JacobiPlus(A , B , 1 , e)
æ0.141414143531829 ö ç-10.3999999977853 ÷
ç 4.80000000125749 ÷ Xk = çç-4.21212121421771 ÷÷
ç -10.399999998345 ÷
ç ÷
è 4.80000000197555 ø
X - двумерный массив, где каждый из его элементов Xk- вектор-столбец, содержащий значения переменных системы, вычисленных на k-ом шаге.
Количество итераций k = 280
Находим вектор невязки:
V := A×Xk - B
æ |
2.43311433223425 |
− 8 |
ö |
ç |
´ 10 |
÷ |
|
ç |
2.74163767244318 |
− 8 |
÷ |
ç |
´ 10 |
÷ |
|
ç |
2.11611075329188 |
´ 10− 8 ÷ |
|
V = ç |
|
− 8 |
÷ |
ç |
|
÷ |
|
ç |
3.61315848351751 |
´ 10− 8 |
÷ |
ç |
2.88109731627628 |
´ 10 |
÷ |
ç |
4.96757870394049 |
− 8 |
÷ |
è |
´ 10 |
ø |
|
Найдем нормы вектора невязки:
Norm1(V) = 1.87526972617036 ´ 10− 7
Norm2(V) = 7.99668814907727 ´ 10− 8
NormInf(V) = 4.96757870394049 ´ 10− 8
Реализуем функцию итерационного алгоритма нахождения корней системы линейных уравнений методом Зейделя:
Zeidel(P , G, p, e) := |
|
min_n_P_val ¬ min_norm (P)1 |
|
|
|
|
|
|||||||||||
|
|
min_n_P_num ¬ min_norm (P)2 |
|
|
|
|
|
|||||||||||
|
|
return |
|
"Не выполняется достаточное условие сходимости!" if min_n_P_val ³ 1 |
||||||||||||||
|
|
X1 ¬ G |
|
|
|
|
|
|
|
|
|
|||||||
|
|
X2 ¬ G |
|
|
|
|
|
|
|
|
|
|||||||
|
|
k ¬ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
m ¬ rows(P) |
|
|
|
|
|
|||||||||||
|
|
for i Î 1 .. m |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
mulsum ¬ 0 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
for |
|
j Î 1 .. m |
|
|
|
|
|
||||||
|
|
|
|
|
|
mulsum ¬ mulsum + Pi , j ×(Xk) |
j |
|
|
|
|
|||||||
|
|
|
|
|
(Xk) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
i |
¬ mulsum + Gi |
|
|
|
|
|
|||||||
|
|
|
|
|
|
é |
|
|
|
|
|
|
|
(1 - min_n_P_val)×e ù |
||||
|
|
while |
|
êNormXëé(Xk - Xk−1), min_n_P_numûù |
³ |
|
ú |
|||||||||||
|
|
min_n_P_val |
||||||||||||||||
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
û |
||||
|
|
|
|
|
k ¬ k + 1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Xk ¬ Xk−1 |
|
|
|
|
|
||||||||
|
|
|
|
|
for |
|
i Î 1 .. m |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
mulsum ¬ 0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
for |
|
j Î 1 .. m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mulsum ¬ mulsum + Pi , j ×(Xk) |
j |
|
|
|
|||
|
|
|
|
|
|
|
|
|
(Xk) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
i |
¬ mulsum + Gi |
|
|
|
|
|
|||
|
|
X |
|
|
if |
p = 0 |
|
|
|
|
|
|
|
|||||
|
|
k |
if |
p = 1 |
|
|
|
|
|
|
|
|||||||
ZeidelPlus(A , B , p, e) := |
|
if |
check_diag_dom(A) ¹ "Есть диагональное преобладание!" |
|
||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
msg ¬ "В матрице A нет диагонального преобладания!" |
|
||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
return msg |
|
|
|
|
|
||||||||
|
|
P ¬ get_P(A) |
|
|
|
|
|
|||||||||||
|
|
G ¬ get_G(A , B) |
|
|
|
|
|
|||||||||||
|
|
Zeidel(P , G, p, e) |
|
|
|
|
|
|||||||||||
X2 := ZeidelPlus(A , B , 0 , e)
k2 := ZeidelPlus(A , B , 1 , e)
æ0.141414142943317 ö ç-10.3999999998001 ÷
ç 4.79999999891466 ÷ X2k2 = çç-4.21212121129192 ÷÷
ç-10.3999999993175 ÷
ç ÷
è 4.79999999931214 ø
æ |
5.23811216623926 |
− 9 |
ö |
ç |
´ 10 |
÷ |
|
ç |
3.35671046514108 |
− 9 |
÷ |
ç |
´ 10 |
÷ |
|
|
´ 10− 9 |
||
ç |
-2.4227686523659 |
÷ |
|
V2 = ç |
-4.62623717112365 ´ 10− 10 |
÷ |
|
ç |
÷ |
||
ç |
|
− 10 |
÷ |
ç |
3.74825503968168 ´ 10 |
÷ |
|
ç |
|
− 14 |
÷ |
è |
-1.06581410364015 ´ 10 |
ø |
|
X - двумерный массив, где каждый из его элементов Xk- вектор-столбец, содержащий значения переменных системы, вычисленных на k-ом шаге.
Количество итераций k2 = 26
Находим вектор невязки:
V2 := A×X2k2 - B
Найдем нормы вектора невязки:
Norm1(V2) = 1.18550511629678 ´ 10− 8
Norm2(V2) = 6.70295807968032 ´ 10− 9
NormInf(V2) = 5.23811216623926 ´ 10− 9
Производим сравнение методов Якоби и Зейделя:
Метод Якоби: |
|
|
Метод Зейделя: |
|
||
k = 280 |
|
|
k2 = 26 |
|
||
æ |
2.43311433223425 |
− 8 |
ö |
æ |
− 9 |
ö |
ç |
´ 10 |
÷ |
ç |
5.23811216623926 ´ 10 |
÷ |
|
ç |
2.74163767244318 |
− 8 |
÷ |
ç |
− 9 |
÷ |
ç |
´ 10 |
÷ |
ç |
3.35671046514108 ´ 10 |
÷ |
|
|
´ 10− 8 |
-2.4227686523659 ´ 10− 9 |
||||
ç |
2.11611075329188 |
÷ |
ç |
÷ |
||
V = ç |
|
´ 10− 8 |
÷ |
V2 = ç |
-4.62623717112365 ´ 10− 10 |
÷ |
ç |
3.61315848351751 |
÷ |
ç |
÷ |
||
ç |
|
− 8 |
÷ |
ç |
− 10 |
÷ |
ç2.88109731627628 |
´ 10 |
÷ |
ç |
3.74825503968168 ´ 10 |
÷ |
|
ç |
|
− 8 |
÷ |
ç |
− 14 |
÷ |
è4.96757870394049 |
´ 10 |
ø |
è |
-1.06581410364015 ´ 10 |
ø |
|
Найдем нормы вектора невязки:
Метод Якоби: |
Метод Зейделя: |
Norm1(V) = 1.87526972617036 ´ 10− 7 |
Norm1(V2) = 1.18550511629678 ´ 10− 8 |
Norm2(V) = 7.99668814907727 ´ 10− 8 |
Norm2(V2) = 6.70295807968032 ´ 10− 9 |
NormInf(V) = 4.96757870394049 ´ 10− 8 |
NormInf(V2) = 5.23811216623926 ´ 10− 9 |
Вывод: Метод Зейделя сходится, в среднем, в два раза быстрее методя Якоби. Но бывают такие входы, на которых метод Зейделя может работать на порядок быстрее (данный вариант), и такие, на которых метод Якоби может быть несколько быстрее метода Зейделя.
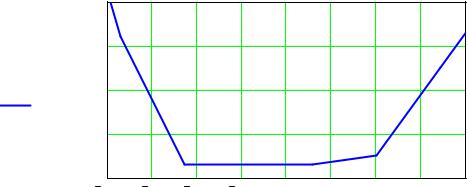
Задача 2.5. Дана система уравнений, представленная в виде Х=PX+G, где P=P(t), t = -1,0.8..0.8,1 -
параметр. Построить график (или гистограмму) зависимости нормы 
 P
P
 C от параметра t. По графику определить, при каких перечисленных выше значениях t выполнено достаточное условие сходимости
C от параметра t. По графику определить, при каких перечисленных выше значениях t выполнено достаточное условие сходимости
итерационных методов. Найти решение системы Х=PX+G методом Якоби с точностью ε =10−5 для наибольшего значения параметра t, при котором выполнено условие сходимости.
Исходные данные:
t := -1 , -0.8 .. 1 Определим диапазон изменения значений t: |
e := 10− 5 |
|
|
|
|
|||||||
|
|
æ0.01 |
0.12 |
0.5 |
-0.1 |
ö |
|
æ3 |
ö |
|||
|
|
ç |
|
|
|
|
÷ |
|
ç |
|
÷ |
|
Определим матрицы P и G: |
P(t) := |
ç-0.1 -0.15 -0.01 |
t2 - 1.5×t ÷ |
G := |
ç |
2 |
÷ |
|||||
ç |
0.15 |
0 |
t |
0.2 |
÷ |
ç |
1 |
÷ |
||||
|
|
|
||||||||||
|
|
ç |
÷ |
|
ç |
|
÷ |
|||||
|
|
è |
0 |
-0.1 |
0.25 |
0.1 |
ø |
|
è0 |
ø |
||
1.1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
NormInf(P(t)) 0.9 |
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
0.70.44 |
0.3 |
0.16 |
0.02 |
0.12 |
0.26 |
0.4 |
0.54 |
|
|
|
|
t |
|
|
|

Определим наибольшее значение параметра t, при котором ещё обеспечивается сходимость итерационного процесса:
t := 0.6 |
|
|
|
X := Jacobi(P(t) , G , 0 , ε) |
æ 5.64141539316748 |
ö |
|
|
|||
|
ç |
0.535589102966324 |
÷ |
|
ç |
÷ |
|
k := Jacobi(P(t) , G , 1 , ε) |
Xk = ç |
5.32541592402732 |
÷ |
|
ç |
|
÷ |
k = 57 |
è |
1.4197721293586 |
ø |
Найдем решение системы для параметра t = 0.2:
t := 0.2 |
|
|
|
|
X := |
Jacobi(P(t) , G , 0 , ε) |
|
|
|
k := |
Jacobi(P(t) , G , 1 , ε) |
æ |
4.2246903036702 |
ö |
ç |
1.24890217604215 |
÷ |
||
|
|
ç |
÷ |
|
k = 19 |
Xk = ç |
2.15724508349516 |
÷ |
|
|
|
ç |
|
÷ |
|
|
è0.460467055240299 |
ø |
|
t =
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Вывод: Если сравнить количество итераций в двух последних проведенных численных экспериментах,то можно сделать вывод, что чем больше значение равномерной нормы матрицы P, тем большее количество итераций требуется для достижения заданной точности.
Задача 2.6. Задана система уравнений AХ=В. Решить систему вручную. Привести данную систему к виду
X=PX+G, готовому для выполнения итерационного процесса. Найти решение системы с заданной
точностью ε =10−6 , используя методы Зейделя и Якоби. Указать количество выполненных итераций для каждого метода. Распечатать промежуточные значения X(k) на промежуточных этапах итерационного процесса. Составить векторы невязки и вычислить их норму. Сделать выводы.
Исходные данные:
|
æ31 |
28 |
19 ö |
|
æ |
2 − N ö |
||
A := |
ç19 |
31 |
21 ÷ |
B := |
ç |
21 |
÷ |
|
|
ç |
|
÷ |
|
ç |
|
|
÷ |
|
è75 |
38 |
48 ø |
|
è |
56 |
ø |
|
|
æ31 |
28 |
19 ö |
|
æ−12 ö |
|
||
A = |
ç19 |
31 |
21 ÷ |
B = |
ç |
21 |
÷ |
|
|
ç |
|
÷ |
|
ç |
|
÷ |
|
|
è75 |
38 |
48 ø |
|
è |
56 |
ø |
|
Найдём точное решение системы средствами целочисленной арифметики, используя метод Гаусса - такой способ решения аналогичен нахождению решения вручную:
A1 := augment(A , B)
|
æ31 |
28 |
19 |
-12 ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
A1 = |
ç19 |
31 |
21 |
21 |
÷ |
|
Расширенная матрица |
|
|
||||||||||||||
|
ç |
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è75 |
38 |
48 |
56 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
get_NOD(a, b) := |
|
NOD ¬ min( |
a |
, |
b |
) |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
while NOD > 1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
break |
if (mod(a, NOD) = 0) Ù (mod(b, NOD) = 0) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
NOD ¬ NOD - 1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
NOD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
GetResultRow (A , n) := |
|
|
for |
j Î 1 .. |
n |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
for i Î 1 .. n |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
C2× j-1, i ¬ Aj+1, i ×A1, 1 - Aj+1, 1×A1, i |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
C2× j, i ¬ A1, 1 if i ¹ 1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ0 |
429 290 |
879 ö |
числитель первой "уничтоженной" строки |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
÷ |
|
C3 := GetResultRow (A1 , 4) |
|
C3 = |
ç0 |
31 |
31 |
31 |
÷ |
общий знаменатель |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ç0 |
-922 |
63 |
2636 ÷ |
числитель второй "уничтоженной" строки |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è0 |
31 |
31 |
31 |
ø |
общий знаменатель |
|
|
æC31, 2 |
C31, 3 |
C31, 4 ö |
|
A2 = |
æ 429 |
290 |
879 ö |
|
|
|||||||||||||
A2 := ç |
|
|
|
|
|
÷ |
|
ç |
|
|
|
÷ |
|
|
|||||||||
|
èC33, 2 |
C33, 3 |
C33, 4 ø |
|
|
|
|
|
|
è-922 |
63 |
2636 ø |
|
|
|||||||||
C2 := GetResultRow (A2 , 3) |
|
C2 = |
æ0 |
294407 |
1941282 ö |
x_NOD3 := C32, 2 x_NOD3 = 31 |
|||||||||||||||||
|
ç |
|
429 |
|
429 |
÷ |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è0 |
|
|
ø |
|
||
|
æ C21, 3 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ç |
|
|
|
÷ |
|
|
æ62622 ö |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
ç x_NOD3 ÷ |
|
|
|
|
|
|
|
|
|
|
||||||||||||
X3 := |
ç C21, 2 |
÷ |
|
|
|
X3 = è 9497 ø |
|
|
|
|
|
|
|
||||||||||
|
ç |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
è x_NOD3 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
æA21, 3×X32 - A21, 2×X31 ö |
x_NOD2 := C22, 2 |
|
x_NOD2 = 429 |
||||||||||||||||||
X2_1 := ç |
|
|
X32×A21, 1 |
÷ |
|
|
|
|
|
||||||||||||||
|
è |
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
æ X2_11 |
ö |
|
|
|
|
|
ç |
|
÷ |
æ-22873 ö |
|
|
X2 := |
x_NOD2 |
|
||||
ç |
|
÷ |
X2 = ç |
÷ |
|
|
|
ç X2_12 |
÷ |
è |
9497 ø |
|
|
|
ç |
|
÷ |
|
|
|
|
|
|
|
|
||
|
è x_NOD2 |
ø |
|
|
|
|
|
|
æA11, 4×X22 |
- A1, 2 X21 |
- A1, 3×X31 |
ö |
|
X1_1 := ç |
|
A1, 1×X22 |
|
÷ |
||
|
è |
|
|
ø |
||
|
æ X1_11 |
ö |
|
|
|
|
|
ç |
|
÷ |
|
|
|
|
|
|
|
|
||
X1 := |
ç x_NOD1 |
÷ |
|
|
|
|
ç X1_12 |
÷ |
|
|
|
||
|
ç |
|
÷ |
|
|
|
|
|
|
|
|
||
|
è x_NOD1 |
ø |
|
|
|
|
æ0 ö
X := ç ÷
è0 ø
æ-21398 ö
ОТВЕТ: X1 = ç ÷
è 9497 ø
X1 := |
X11 |
|
|
|
|
X12 |
|
|
|
||
|
|
|
|
||
|
æ31 |
28 |
19 ö |
||
ПРОВЕРКА: |
A = ç |
19 |
31 |
21 ÷ |
|
|
ç |
|
|
÷ |
|
|
è75 |
38 |
48 ø |
||
V_Gauss := A×X - B
x_NOD1 := A1, 1 |
x_NOD1 = 31 |
æ-22873 |
ö |
æ62622 |
ö |
||
X2 = ç |
9497 |
÷ |
X3 = ç |
9497 |
÷ |
è |
ø |
è |
ø |
||
X2 := |
X21 |
|
X3 := |
X31 |
||||
X22 |
X32 |
|||||||
|
|
|
|
|||||
|
æ-12 ö |
|
æ-2.25313256817943 ö |
|||||
B = |
ç |
21 ÷ |
|
X = ç-2.40844477203327 |
÷ |
|||
|
ç |
÷ |
|
ç |
|
÷ |
||
|
è |
56 ø |
|
è 6.59387174897336 |
ø |
|||
|
|
æ |
− 15 |
ö |
||||
|
|
|
|
|
-3.5527136788005 ´ 10 |
|
|
|
|
|
ç |
− 15 |
÷ |
||||
V_Gauss = ç |
-3.5527136788005 ´ 10 |
|
÷ |
|||||
|
|
ç |
− 14 |
÷ |
||||
|
|
è |
-1.4210854715202 ´ 10 |
|
ø |
|||
Найдем нормы вектора невязки:
Norm1(V_Gauss) = 2.1316282072803 ´ 10− 14
Norm2(V_Gauss) = 1.50728876033642 ´ 10− 14
NormInf(V_Gauss) = 1.4210854715202 ´ 10− 14
