Mathcad - ЛР4-1

Министерство образования Российской Федерации Санкт - Петербургский государственный политехнический университет

Институт менеджмента и информационных технологий

Кафедра ПО ВТ и АС

Лабораторный практикум по курсу вычислительной математики

ОТЧЕТ

по лабораторной работе №4 (Часть I)

Тема:

ПРИБЛИЖЕНИЕ ФУНКЦИЙ

Выполнил: _______________

Группа: _____

Вариант: 14

Проверил: Царев В.А.

Отметка о зачете __________________

" ___ " ______________ 2006 г.

Череповец

2006

Задача 4.1. Функция y=f(x). Приблизить f(x) на отрезке [a,b] интерполяционными многочленами (в форме Лагранжа и Ньютона) степени n по значениям в заданных n+1 узлах: a £ x0 < x1 < ... < xn £ b . Оценить

погрешность приближения. Решить задачу интерполяции и экстраполяции в заданных узлах xint и xextr .

Найти абсолютную и относительную ошибку интерполяции и экстраполяции. Порядок решения задачи:

1.Найти значения функции в заданных узлах (x0 , f (x0 )),(x1 , f (x1 )),...,(xn , f (xn )) . Составить программу, возвращающую значения интерполяционного многочлена (отдельно для формы Лагранжа Ln (x) и для формы Ньютона Hn (x) ) по полученной таблице.

2. Вывести на один чертеж графики функций f (x) , Ln (x) и Hn (x) .

3.Оценить погрешность приближения функции Dn ( f (x)) интерполяционным многочленом. Для этого построить график абсолютной ошибки ε(x) = f (x) - Ln (x) на отрезке [a,b] и оценить по

графику Dn ( f (x)) = max ε (x) .

x [a,b]

4.Вычислить значения многочлена Ньютона Hn (x) в заданных точках xint и xextr . Приняв значение

многочлена Лагранжа за приближенное значение функции рассчитать абсолютную и относительную погрешность интерполяции и экстраполяции по сравнению с точным значением функции f (x) в этих точках. Определить количество верных цифр в полученных приближениях.

Исходные данные:

f(x) := x− 3 ex

n := 5

i := 0.. n

æ 0.5 ö

æ 13.189770165601 ö

ç

0.75

÷

ç

5.01807411345227

÷

ç

1

÷

yi := f(xi)

ç

2.71828182845905

÷

ç

÷

ç

÷

x := ç

1.25

÷

y =

ç

1.78705559422046

÷

ç

÷

ç

÷

ç

1.3

÷

ç

1.67013958471518

÷

è 1.4 ø

è1.47784255351482 ø

Решение задачи:

N(x, y,n, t) :=

for

i Î 0.. n

fi , 0 ¬ yi

L(x,y, n,t) :=

s ¬ 0

for

kÎ 1.. n

for i Î 0.. n - k

for i Î 0.. n

(fi+1, k−1 - fi , k−1)

p ¬ 1

fi , k ¬

- xi

for j Î 0.. n

xi+k

p ¬ p ×

t - xj

if j ¹ i

s ¬ y0

x

- x

j

for

kÎ 1.. n

i

r ¬ 1

s ¬ s + p × yi

for i Î 0.. k - 1

s

r ¬ r × (t - xi)

s ¬ f0, k × r + s

s

Вычисление значений интерполяционного многочлена в точках tk на отрезке
[a,b]:		b := 1.5
a :=	0.5
			b - a					:= L(x,y, n,tk)
k :=	0.. 100	tk := a +	100 × k	LAGRANGEk
				NEWTON		k	:=	N(x, y, n, t )
								k
График интерполяционного многочленa и точечный график исходной функции:
		10							10
LAGRANGEk								NEWTONk
yi								yi
		5							5
		0.5		1				1.5	0.5	1	1.5
				tk, xi						tk, xi
		e(z) :=	f(z) - L(x, y,n, z)		e1k := e(tk)
	ε(z)	0			D := max(e1)
		0.5	1	1.5
			z
Максимальная абсолютная погрешность приближения:									D = 0.228189032193789
Значение интерполяционного многочлена в форме Ньютона в точках xint и xext:

N(x, y,n, 1.2) = 1.92384456759507

N(x, y,n, 1.45) = 1.38422235818436

Значения функции f в этих точках:

f(1.2) = 1.92136395991698

f(1.45) = 1.39837287799215

true_digits(True, Current) :=

D ¬

True - Current

Temp ¬

Current

Current ¬

Current

k ¬ 10

i ¬ 0

while Temp ³ 0.1

if Temp ³ 1

k

i ¬ i + 1

k ¬ k × 10

Temp ¬ Current - floor(Temp)

Temp2 ¬ Temp

j ¬ 0

while floor(Temp) ¹ Temp2

Temp ¬ Temp × 10

Temp2 ¬ Temp2 × 10

j ¬ j + 1

m ¬ 0

Digit ¬ 10i−1

for p Î 0.. i - 1

m ¬ m + 1

if

Digit > D

2

Digit ¬ Digit

10

n ¬ 0

Digit ¬ 0.1

for p Î 0.. j

n ¬ n + 1

if

Digit > D

2

Digit ¬ Digit

10

m + n

D(True, Current) :=

True - Current

Абсолютная погрешность

d(Current, D) :=

D

Относительная погрешность

Current

Погрешности многочлена Лагранжа в точках xint и xext:

D(f(1.2) , L(x, y,n, 1.2)) = 0.002480607678091 d(L(x, y,n, 1.2) ,D(f(1.2) , L(x, y,n, 1.2))) = 0.001289401295653

D(f(1.45) , L(x, y, n, 1.45)) = 0.014150519807784 d(L(x, y,n, 1.2) ,D(f(1.2) , L(x, y,n, 1.2))) = 0.001289401295653 true_digits(f(1.2) , L(x, y, n, 1.2)) = 3

true_digits(f(1.45) ,L(x,y, n,1.45)) = 2

Вывод: Погрешность интерполяции и экстраполяции, выполненных в конце данного задания достаточно низка, что объясняется достаточно простым поведением

приближаемой функции и незначительынм удалением узла экстраполяции от отрезка приближения. Многочлены в форме Лагранжа и Ньютона совпали, что подверждает правильность выполнения задачи интерполяции.

Задача 4.2. Функция f (x) задана табличным образом

(x0 , f (x0 )),(x1 , f (x1 )),...,(xn , f (xn )) .

Одно значение			f (xi ) для точки xi		упущено. Восстановить это значение при помощи интерполяционного
многочлена P(x) минимально возможной степени (в форме Лагранжа или Ньютона).
Исходные данные:
æ	-3	ö	æ	0.262	ö
ç	-2.55	÷	ç	-1.032	÷
ç		÷	ç		÷
ç	-2.1	÷	ç	-1.747	÷
ç		÷	ç		÷
ç	-1.65	÷	ç	-1.981	÷
ç	-1.2 ÷		ç	-0.564 ÷
ç	-0.75	÷	ç	0.774	÷
x := ç	-0.3	÷	y := ç	2.400	÷
ç		÷	ç		÷
ç 0.15 ÷			ç	2.131	÷
ç	0.6	÷	ç	2.2	÷
ç	1.05	÷	ç	-0.393	÷
ç		÷	ç		÷
ç	1.95	÷	ç	-0.788	÷
ç		÷	ç		÷
è	2.4	ø	è	8.030 ø

Решение задачи:

n := 11
a := -3	b := 2.4			i := 0.. n
k := 0.. 400	tk := a +	b - a	× k	LAGRANGEk := L(x,y, n,tk)
		400

[a,b]

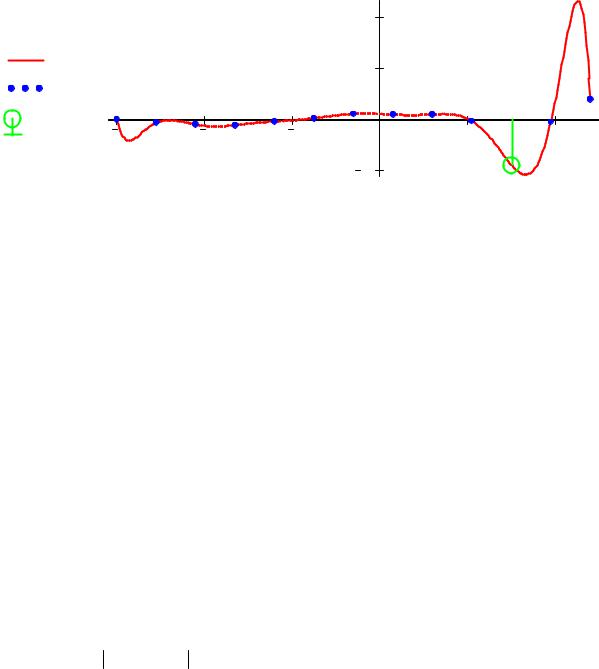
График интерполяционного многочленa и точечный график исходной функции:

			40
LAGRANGEk
yi			20
L(x, y, n, 1.5)
3	2	1	0	1	2

20

tk, xi, 1.5

L(x,y, n,1.5) = −17.6328787878788 Искомое значение в точке х11

Вывод: Минимально-возможная степень многочлена Лагранжа достигается при использовании всех представленных значений неизвестной функции, т.к. при использовании не всех представленных узлов (например, двух) степень интерполируемой функции не будет отражена вообще.

Задача 4.3. Функция f (x) задана на отрезке [a,b]. Построить интерполяционные многочлены Pk (x) ,

k =1,2,3,4 (в форме Лагранжа или Ньютона), по равноотстоящим узлам для различных шагов

дискретизации hk . Для каждого варианта приближения функции

f (x)

оценить погрешность приближения.

Порядок решения задачи:

b - a

b - a

b - a

1)

Для каждого значения h

k

,

k =1,2,3,4 , где h

= b - a ,

h

=

, h

=

,

h

=

.

2

3

4

1

2

3

4

А) Определить интерполяционные узлы a £ x0

< x1 < ... < xn

£ b , где n = k +1,

xi

= a + hk ×i ,

i = 0..n .

В) Составить таблицу (x0 , f (x0 )),(x1 , f (x1 )),...,(xn , f (xn )) .

С) По таблице построить интерполяционный многочлен Pk (x)

(в форме Лагранжа или Ньютона).

2)

Вывести на одном чертеже график функции f (x) и графики всех интерполяционных многочленов

Pk (x) , k =1,2,3,4 .

3)Вывести на другом чертеже графики функций погрешностей приближения

εk (x) = f (x) - Pk (x) . Графически оценить максимальные погрешности приближения каждого

многочлена в пределах заданного отрезка по формуле

Dk	( f (x)) = max ε k	(x) = max		f (x) - Pk (x)		.
	x [a,b]	x [a,b]

Исходные данные:

x := 0 y := 0

a := 0	b := 2	Концы отрезка
f(x) := x + e− x2

Решение задачи:

Определяем узлы интерполяции, строим таблицу значений функции:

k := 1

hk :=

b - a

i := 0.. k

xi := a + hk × i

yi := f(xi)

k

æ

0

ö

æ

1

ö

F

:= x

F

:= y

x = ç ÷

y = ç

÷

è

2

ø

è2.01831563888873

ø

i , 0

i

i , 1

i

F =

0

1

0

0

1

1

2

2.018

Определяем погрешность:

e1(z) :=

f(z) - L(x, y, 1, z)

k := 2

hk :=

b - a

i := 0.. k

xi := a + hk × i yi := f(xi)

k

æ0 ö

æ

1

ö

x = ç

1 ÷

y = ç

1.36787944117144

÷

F

0

:= x

F

1

:= y

ç ÷

ç

÷

i ,

i

i ,

i

è

2 ø

è

2.01831563888873 ø

0

1

F =

0

0

1

1

1

1.368

2

2

2.018

e2(z) :=

f(z) - L(x, y, 2, z)

k := 3

hk :=

b - a

i := 0.. k

xi := a + hk × i

yi := f(xi)

k

æ

0

ö

æ

1

ö

ç

0.666666666666667

÷

ç

1.30784705509662

÷

x =

ç

÷

ç

÷

F

:= x

F

:= y

ç

y =

ç

÷

1.33333333333333

÷

1.5023466487394

i , 0

i

i , 1

i

ç

÷

ç

÷

è

2

ø

è2.01831563888873 ø

0

1

0

0

1

F =

1

0.667

1.308

2

1.333

1.502

3

2

2.018

e3(z) :=

f(z) - L(x, y, 3, z)

k := 4

	h :=	b - a
		k
	k

æ 0 ö

ç ÷

ç0.5 ÷ x = ç 1 ÷

çç1.5 ÷÷

è 2 ø

i := 0.. k xi := a + hk × i			yi := f(xi)
æ	1	ö
ç	1.2788007830714	÷
ç		÷
y = ç	1.36787944117144	÷	F	:= x	F	:= y
ç	1.60539922456186	÷	i , 0	i	i , 1	i
ç	2.01831563888873	÷
è		ø

			0		1
	0		0		1
F =	1		0.5		1.279
	2		1		1.368
	3		1.5		1.605
	4		2		2.018
e4(z) :=				f(z) - L(x, y, 4, z)

Вычисление значений интерполяционного многочлена в точках tk: на отрезке

	[a,b]:		b - a
	j := 0.. 100	tj := a +		× j
			100

q1j := L(x, y, 1,tj) q2j := L(x, y, 2,tj) q3j := L(x, y, 3,tj) q4j := L(x, y, 4,tj)

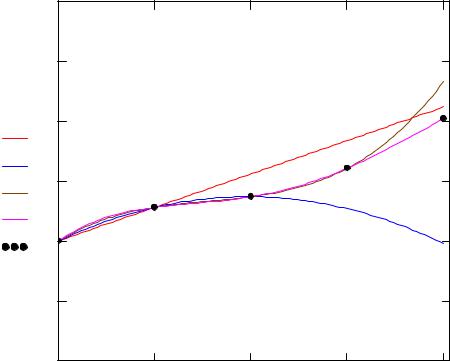
	3
	2.5
q1j	2
q2j
q3j	1.5
q4j
yi	1
	0.5
	0 0	0.5	1	1.5	2
			t j, t j, t j , t j , xi

Графики интерполяционных многочленов и график исходной функции

Вычисление погрешностей интерполяционного многочлена в точках tk: на отрезке

	[a,b]:		b - a
	j := 0.. 100	tj := a +		× j
			100

e1j := e1(tj)

e2j := e2(tj)

e3j := e3(tj)

e4j := e4(tj)

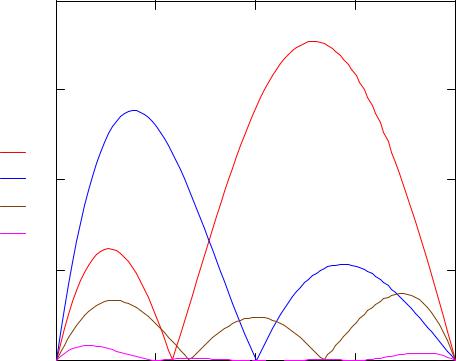
0.15
e1 j
e2 j
0.1
e3 j
e4 j
0.05
0 0	0.5	1	1.5	2
		t j, t j , t j , t j

Графики погрешностей

Максимальные погрешности приближения:

1 := max(e1)	1	= 0.177431350103302
2 := max(e2)	2	= 0.139032460497719
3 := max(e3)	3	= 0.037340835076735
4 := max(e4)	4	= 8.44077455073133 × 10− 3

Вывод: Как видно из результатов вычислительного эксперимента, наименьшая

погрешность интерполяции достигается при использовании наибольшего возможного количества узлов.