§2. Построение эмпирических моделей по данным пассивного эксперимента

Оглавление

2.1. Определение вида приближённого уравнения регрессии

В общем случае необходимо анализировать графики зависимостей экспериментальных данных выходных переменных y от входных x и по их виду выбирать конкретную форму функциональной зависимости (3).

Преобразование системы координат y – x даёт возможность выбрать оптимальный вид функциональной зависимости (3).

Для случая одной входной переменной х по опытным данным рекомендуется построить эмпирическую линию регрессии (рис.1) и с её помощью выбирать конкретный вид функции (3).

Изображение эмпирической линии регрессии:

При этом весь диапазон изменения x (рис.1) разбивается на s равных интервалов Δx. Все точки, попавшие в данный интервал Δx_j , относят к его середине x_j^* . После этого подсчитывают частные средние y_j^* для каждого интервала:

где n_j – число точек в интервале Δx_j.

В результате объём выборки определяется по формуле:

Эмпирическая линия регрессии y по x получается в виде ломанной линии путём последовательного соединения отрезками прямой линии точек:

При выборе вида функции (3) для случая нескольких входных переменных

может быть применён метод Брандона, который здесь не рассматривается.

В общем случае различают два вида уравнений регрессии (эмпирических моделей) – нелинейные по параметрам , статистический анализ которых осуществляется методом «нелинейной регрессии» и линейные по параметрам , статистический анализ которых проводится методом «линейной регрессии».

Линейные по параметрам модели могут быть представлены в следующем виде:

где - линейные или нелинейные функции входных переменных ().

Определение параметров (коэффициентов) линейных моделей и их регрессионный анализ существенно проще, чем для нелинейных моделей.

Поэтому нелинейные модели, по возможности, стараются линеаризовать и привести к виду (6).

Частными случаями уравнения линейной регрессии являются:

• полиномиальная регрессия, когда

и её разновидности – линейная регрессия от одной переменной ( m=1 ):

и параболическая регрессия ( m=2 ):

• трансцендентная регрессия и её разновидности в виде зависимости показательного типа:

которая линеаризуется логарифмически:

и дробно-показательного типа:

которая также линеаризуется логарифмически:

• множественная регрессия, когда число входных переменных больше 1:

Оглавление

2.2. Определение коэффициентов регрессии – параметров эмпирических моделей (выполнение первого этапа регрессионного анализа).

В соответствии с методологией регрессионного анализа в этом случае решается задача аппроксимации экспериментальных данных методом наименьших квадратов (МНК).

На рисунке приведена графическая интерпретация МНК для случая регрессии от одной переменной х ( * - экспериментальные данные, - расчётные данные по уравнению регрессии):

При этом эксперимент проводится с использованием следующей таблицы:

Вид функции одной переменной может быть выбран (решение задачи структурной идентификации) путём преобразования осей координат у – х как показано ниже.

В результате преобразованная функция у становится линейной не только по коэффициентам регрессии, но и по преобразованной переменной х .

Преобразования к линейному виду функций одной переменной.

Уравнение	Координаты прямой		Уравнение прямой	Замечания
	ось x	ось y
	x			Асимптоты:
		y		Асимптоты:
				Асимптоты:
или
или
	x	где - любая точка на экспериментальной кривой		Асимптоты: Та же кривая, что и в 3), сдвинутая вверх или вниз на расстояние .
	log x	log y		Если , кривая имеет вид параболы и проходит через начало координат и точку . Если , кривая является гиперболой с осями координат в качестве асимптот и проходит через точку .
	log x			Сначала аппроксимируют по формуле , где , а - экспериментальные точки.
	log x			После логарифмирования исходного уравнения поступают, как в п. 4а)
	x	log y		Кривая проходит через точку .

Критерий МНК имеет вид:

где и рассчитываются при одном и том же значении элементов вектора

n – общее число опытов или объём выборки.

Согласно уравнению (3) и поэтому критерий Cr также является функцией многих переменных от параметров :

Для определения (подгонки) коэффициентов (параметров) модели (3) необходимо, чтобы критерий Cr стал наименьшим, т.е. чтобы сумма квадратов вертикальных отрезков на рисунке стала наименьшей:

Поэтому задача определения коэффициентов модели (3) сводится к реализации одного из алгоритмов оптимизации для определения минимума критерия (15) и (16):

- допустимая область изменения параметров - ограничения первого рода.

Именно так решается задача параметрической идентификации для нелинейных моделей.

Конечно, в данном случае возможно также воспользоваться необходимым условием экстремума функции многих переменных (16):

Для определения искомых коэффициентов система в общем случае нелинейных уравнений (18) должна быть решена относительно коэффициентов a₀, a₁,…a_m.

Однако, как показывает практика, решение систем нелинейных уравнений ничуть не проще, чем прямое решение задачи оптимизации (17).

Определение выборочных (эмпирических) коэффициентов регрессии

для линейных по параметрам моделей (произвольное число входных переменных

Таблица проведения экспериментальных исследований в этом случае имеет вид:

Для линейных или линеаризованных по параметрам моделей необходимо выражение (6) подставить в критерий МНК (15):

и, воспользовавшись необходимым условием экстремума функции многих переменных (18), решать полученную систему линейных алгебраических уравнений (СЛАУ):

Перегруппировав члены в системе уравнений (20), можно записать СЛАУ в виде:

И если ввести в рассмотрение информационную матрицу :

то она окажется квадратной, симметричной и значения её элементов зависят только от входных переменных и конкретного вида функций .

В матричном виде информационную матрицу можно представить в виде произведения трансформированной и исходной матрицы входных переменных :

Матрица, зависящая от входных переменных, имеет вид:

Соответственно правую часть СЛАУ (21) можно записать:

или в матричном виде:

В результате СЛАУ (21), решаемая для определения коэффициентов эмпирической модели, может быть представлена:

или в матричном виде:

Если для определения коэффициентов использовать метод обратной матрицы, то получится:

и так как произведение равно единичной матрице , т.е.

то

или

Матричная формула для определения коэффициентов линейной регрессии (параметров эмпирической модели) получается после подстановки в (32) матричных равенств (23) и (26):

Таким образом для определения коэффициентов линейной или линеаризованной регрессионной модели необходимо выполнить следующую последовательность действий:

• сформировать вектор наблюдений 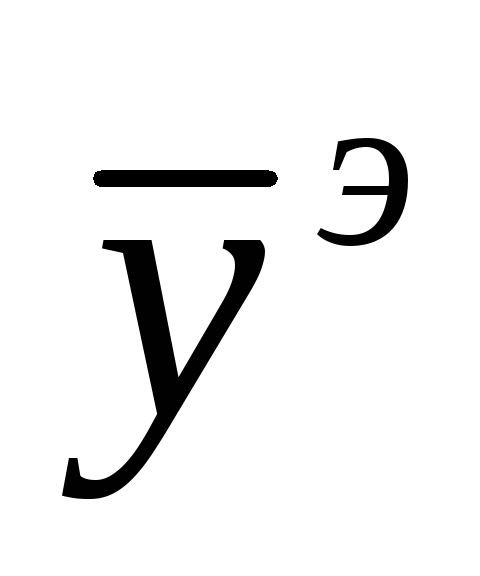и вычислить его компоненты (только для линеаризованных моделей);

• сформировать и рассчитать компоненты матрицы, зависящей от входных переменных;

• транспонировать матрицу ;

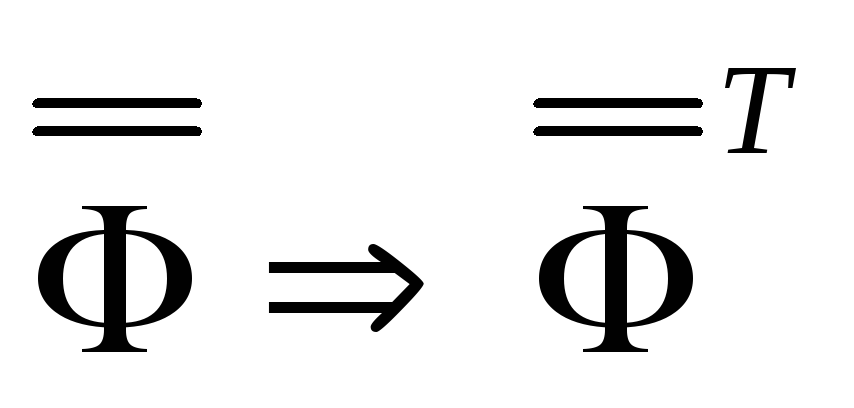• перемножить транспонированную матрицу на исходную матрицу ;

• выполнить обращение информационной матрицы - ;

• умножить полученную обратную матрицу на матрицу ;

• умножить полученный результат на вектор наблюдений и получить выборочные коэффициенты регрессии (33).

Оглавление

Продолжение Темы 07

Вернуться к списку лекций