Разностные схемы

второго и выше порядков аппроксимации. Схемы первого порядка обладают аппроксимационной вязкостью, которая порождается самой структурой разностной схемы.

Рассмотрим включение искусственной вязкости в схему Лакса-Вендроффа. В простейшем случае можно положить B(s)=I и для сохранения второго порядка аппроксимации μ=μa(t)h2. Тогда вязкостный член примет вид

μa (t)h2 ∂2 s .

∂x2

Аналогичные выражения описывают вязкие силы при движении вязкой жидкости, но в отличии от реальной вязкости, искусственная вязкость исчезает при h→0. Аппроксимируя вторую производную в момент времени tk, получим схему Лакса-Вендроффа для системы

(6.8):

snk +1 = snk − τk ( fnk++1/1/22 − fnk−+1/1/22 )+ μak τk (snk+1 − 2snk + snk−1 ),

(6.9)

h

n=1, …, N-1

где

ν = μkaτk

постоянный малый параметр. Величина параметра ν подбирается экспериментально, так как она зависит от конкретной задачи и шага разностной сетки.

Введение искусственной вязкости иногда бывает необходимым для получения устойчивого процесса вычислений. Дело в том, что анализ устойчивости схемы (6.3) проводился для уравнений линеаризованных в окрестности течения с постоянными параметрами и не учитывал нелинейных эффектов, которые в ряде случаев являются источником неустойчивости. Такая неустойчивость называется нелинейной. Для предотвращения этого явления в некоторых задачах оказалось необходимым введение в

разностную схему дополнительных слагаемых, определяющих искусственную вязкость. Так нетрудно получить, что схема (6.9) требует более строгого ограничения на шаг по времени:

τk ≤ τmax 1 − 2ν .

Вообще говоря, включение искусственной вязкости в неустойчивую схему может сделать эту схему устойчивой.

101

_____________________________________________________________________________

Пример 6.2. (схема Лакса-Вендроффа с искусственной вязкостью)

Рассмотрим задачу Сода с начальными условиями (6.7). Только теперь для решения этой задачи применим схему (6.9). Результаты расчётов показаны на рисунках 6.5-6.8.

Эти результаты показывают, что введение искусственной вязкости позволяет подавлять нефизические осцилляции приближённого решения, хотя это достигается за счёт некоторого размазывания разрывов.

Рисунок 6.5. Пространственное распределение плотности в момент времени t=0.5046 ; -

точное решение, - приближённое решение (схема Лакса-Вендроффа, h=0.02, ν=0.06).

________________________________________________________________________________

6.3. Задача о распаде разрыва.

В Главе 5 мы рассмотрели задачу о распаде разрыва для уравнений акустики, которая имеет довольно простое решение. Аналогичная задача может быть сформулирована и для уравнений газовой динамики. Однако, даже в случае простейшего уравнения состояния идеального газа (который мы рассмотрим), аналитическое решение не всегда может быть получено.

Течение газа определяется тремя независимыми переменными

ρ w = u

p

102

и постоянной γ, которая характеризует конкретный газ. Тогда задачу о распаде разрыва можно сформулировать следующим образом: пусть в момент времени t=0 распределение газодинамических величин имеет вид

w ( x,0 ) = wL , x ≤ 0 ,

wR , x > 0

где

		ρL
wL =			и wR
	uL
		pL

ρR

=uR

pR

постоянные векторы. При t>0 это состояние распадается на две волны, которые разделены контактной поверхностью. В зависимости от начальных данных могут возникать либо ударные волны либо волны разрежения. Возможные комбинации показаны на рисунке 6.9, где отмечены положения фронта волны или контактного разрыва на (x,t) диаграмме. Задача Сода, расмотренная в примере 6.1, является примером конфигурации 2 и на рисунках 6.1-6.4 показано распределение газодинамических величин при распространении волны разрежения, ударной волны и контактного разрыва. Следует заметить, что кофигурация 5 теоретически возможна для идеального газа, но в такой ситуации сама модель идеального газа не применима. Поэтому в реальности такая конфигурация осуществиться не может.

103

Рисунок 6.9. Пять возможных кофигураций решения задачи о распаде разрыва; S – обозначает ударную волну; R - волну разрежения; C - контактный разрыв.

Для решения задачи о распаде разрыва необходимо определить шесть неизвестных величин

		ρOL
wOL =				и wOR
	uOL
		p
		OL

ρOR

=uOR

pOR

по обе стороны от контактного разрыва. Эти величины выражаются через известные состояния wL и wR либо через соотношения Ренкина-Гюгонио для ударной волны, либо через изэнтропические характеристические уравнения для волны разрежения. Учитывая, что только плотность претерпевает разрыв на контактной поверхности, а скорость и давление непрерывны, то есть uOL=uOR=uO и pOL=pOR=pO, уравнения описывающие решение задачи о распаде разрыва сводятся к одному нелинейному алгебраическому уравнению. В общем случае это уравнение может быть решено итерационным методом. Только в случае однокомпонентной среды кофигурация 4 допускает аналитическое решение. Более подробное описание процедуры решения задачи о распаде разрыва приведено в Приложении

B.

В последующих параграфах решение задачи о распаде разрыва будет использоваться для построения численных схем расчёта газодинамических течений. Так в схеме С. К. Годунова используется только решение в точке x=0. В методе взвешенного усреднённого потока используется также информация и о структуре течения, возникающего после распада разрыва.

104

6.4.Схема С. К. Годунова.

Впараграфе 5.6 мы рассмотрели схему С. К. Годунова для уравнений акустики. Аналогичные принципы могут быть использованы и для построения разностной схемы для уравнений газовой динамики.

Введём разностную сетку с узлами (xn, tk), где xn=nh, n=0, 1, … Интегрирование уравнений (6.1) по разностной ячейке даёт следующую схему

sk +1	− sk	+1/ 2 +		f (snk+1 )− f (snk )	= o .
n+1/ 2	n
	τk			h

и tk+1=tk+τk.

(6.10)

n=0, …, N-1

Полуцелые индексы обозначают средние на интервале значения, которые определяют приближённое решение в виде кусочно-постоянной функции (рисунок 5.10). В момент времени tk такая функция известна. За время порядка τk≤τmax поведение этой системы также известно: каждый разрыв немедленно распадается с образованием ударных волн или волн разрежения, как показано на рисунке 6.9. Тогда полагая

w = wk−1/ 2 и w = wk+1/ 2 , n

R

n

L

из решения задачи о распаде разрыва мы получим

wnk = w (0,τk )

в каждом узле xn. Так как s выражается через w, то величины

f (snk ), n=0, …, N (6.11)

определяются из соотношений (6.2). Вычисление одного шага по времени завершается определением решения в момент времени tk+1 из схемы (6.10). Анализ аппроксимации показывает, что эта схема аппроксимирует уравнения (6.1) с первым порядком по h и τ. Шаг по времени задаётся соотношением (6.6).

Граничные условия учитываются при расчёте величин (6.11) при n=0 и n=N. Мы рассмотрим два типа граничных условий: твёрдая стенка (или ось симметрии) и открытая граница расчётной области. В качестве примера рассмотрим расчёт этих условий на левой границе расчётной области при x=0. Для этого введём фиктивный слой с некоторым состоянием w-1/2. Для граничного условия на твёрдой стенке u(0,t)=0 это фиктивное состояние определяется из известного состояния в соседней правой ячейке следующим образом

105

		ρ		k		ρk
							1/ 2
wk	= u				=		−uk
−1/ 2							1/ 2
		p					pk
			−1/ 2				1/ 2

После решения задачи о распаде разрыва с

wL = w−k1/ 2 и wR

k=0, 1, … .

= w1/k 2

мы получим решение в граничном узле. В случае открытой границы, когда газ истекает из области, можно положить

w−k1/ 2 = w1/k 2 ,

что даёт тривиальное решение и никаких волн, которые могли бы исказить решение внутри области, не возникает.

________________________________________________________________________________

Пример 6.3. (схема С. К. Годунова)

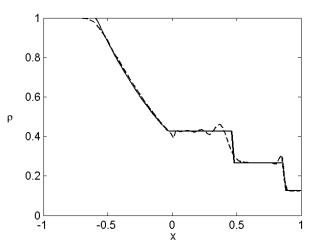
Применим схему (6.10) к задаче Сода с начальными условиями (6.7). Результаты расчета показаны на рисунках 6.10-6.13.

Рисунок 6.10. Пространственное распределение плотности в момент времени t=0.5027 ;

- точное решение, - приближённое решение (схема С. К. Годунова, h=0.02).

Так как схема С. К. Годунова является схемой первого порядка аппроксимации, то в областях непрерывного течения она даёт менее точное решение по сравнению, например, со схемой Лакса-Вендроффа. В области ударного скачка решение имеет довольно крутой профиль и колебаний за фронтом скачка не возникает. Поэтому этот метод успешно применяется для расчёта сильных ударных волн.

________________________________________________________________________________

106

6.5. Метод взвешенного усреднённого потока.

Метод взвешенного усреднённого потока (WAF, Weighted Average Flux) представляет собой один из способов модификации метода С. К. Годунова для того, чтобы получит схему второго порядка точности. Основная идея этого метода, по сути дела, была рассмотрена в пункте 5.6.2 применительно к уравнениям акустики. Рассмотрим теперь реализацию этого подхода в случае уравнений газовой динамики. Основная схема метода WAF по своей структуре совпадает со схемой (6.10):

sk +1

− sk

−

f (snk+1 )− f (snk )

= o ,

n+1/ 2

n+1/ 2

τk

h

n=0, …, N-1,

где

k

k

k

1 xn +h / 2

sn

= s(wn

),

wn

=

∫ w(x,tk + 0.5τk ) dx .

h

xn −h / 2

(6.12)

(6.13)

Здесь w(x,t) обозначает решение задачи о распаде разрыва с начальными данными

(wk− , wk+ ).

n 1/ 2 n 1/ 2

Так как при распаде разрыва образуется одна из четырёх конфигураций течения, то вычисления интеграла (6.13) имеет ряд особенностей для каждой из этих конфигураций. Поэтому мы рассмотрим подробно два случая, а затем получим общую формулу.

В случае кофигурации 1 (две ударные волны) решение имеет вид показанный на рисунке 6.14 (здесь и далее используются обозначения введённые в Приложении B) и интеграл (6.13) легко вычисляется:

wnk = 1h (| d1 − d2 | wL + | d2 − d3 | wOL + | d3 − d4 | wOR + ,

| d4 − d5 | wR )

где координаты dp (p=1, …, 5) отсчитываются от точки xn и равны

d1 = −12 h , d2 = 12 c1τk , d3 = 12 c3τk , d4 = 12 c5τk , d5 = 12 h .

107

Рисунок 6.14. Схематическое представление решения задачи о распаде разрыва в случае конфигурации 1; c1, c5 – скорости ударных волн, c3 – скорость контактного разрыва. Для более компактной записи введём следующие обозначения

w(1)=wL , w(2)=wOL , w(3)=wOR , w(4)=wR ,

и запишем предыдущую формулу в виде

k		1	4	( p)
wn	=		∑αp w		,	(6.14)
		2 p=1

где коэффициенты αp выражаются следующим образом

	α1 =1 +		c1τk			=1 + β1 ,
				h
α	2	= τk (c		− c			) = β	2	−β	,	(6.15)
		h	3	1					1
α3 =		τk (c5 − c3 ) = β3 −β2 ,
		h

α4 =1 − c5hτk =1 −β3 .

Для конфигурации 2 (волна разрежения-ударная волна) решение имеет вид показанный на рисунке 6.15. Вычисление интеграла (6.13) в этом случае требует интегрирования решения вдоль волны разрежения. В приципе, это можно сделать точно, так как решение wFL(x,t) известно (смотри (В.8) в Приложении B).

108

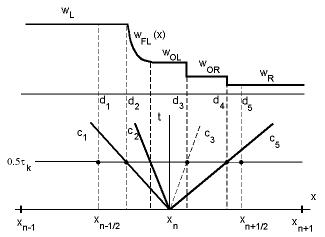
Рисунок 6.15. Схематическое представление решения задачи о распаде разрыва в случае конфигурации 2.

Для упрощения вычислений и уменьшения числа операций обычно прибегают к приближённой оценке интеграла по области содержащей волну разрежения. Так интеграл по отрезку [d2, d3] вычисляется следующим образом:

d3		wOL , c2 < 0
∫ w(x,tk + 0.5τk ) dx =| d2	− d3			.
		|
d2		wFL (0,t), c2	> 0

Вычисление остальных частей интеграла (6.13) производится также как и в предыдущем случае и окончательный результат можно представить в виде (6.14), где

w(2)	wOL , c2 < 0		.
	=	> 0
	wFL (0,t), c2

Общая формула для вычисления усреднённого значения имеет вид (6.14), только компоненты w(p) определяются в зависимости от конфигурации решения. Компоненты w(1) и w(4) одинаковы для всех кофигураций:

w(1)=wL , w(4)=wR ,

а компоненты w(2) и w(3) определяются следующим образом: 1) конфигурация 1

		w(2)=wOL , w(3)=wOR ;
2) конфигурация 2
w(2)		wOL , c2	< 0		(3)
		=		, w =wOR;
		wFL (0,t), c2 > 0
3) конфигурация 3
w	(2)		wOR , c4		> 0	;
	=wOL , w(3)		=
			wFR (0,t), c4 < 0

4) конфигурация 4

109

w(2)	wOL , c2 < 0		, w(3)	wOR , c4 > 0		.
	=	> 0		=	< 0
	wFL (0,t), c2			wFR (0,t), c4

Коэффициенты αp (p=1, …, 4) определяются выражениями (6.15), только скорости c1 и c5 имеют разный смысл для различных кофигураций (смотри Приложение B).

Представленная схема метода WAF аппроксимирует уравнения (6.1) со вторым порядком по h и τ. Шаг по времени выбирается из условия (6.6). Для расчёта граничных условий применяется такой же подход, что и в схеме С. К. Годунова.

________________________________________________________________________________

Пример 6.4 (схема метода WAF)

Применим схему (6.12) к задаче Сода с начальными условиями (6.7). Результаты расчета показаны на рисунках 6.16-6.19.

Как и следовало ожидать, эти результаты напоминают приближённое решение полученное с помощью схемы Лакса-Вендроффа. Обе схемы имеют второй порядок аппроксимации, поэтому в областях, где точное решение изменяется непрерывным образом, приближённое решение вычисляется достаточно точно. В областях, где точное решение изменяется резко, приближённое решение проявляет осциллирующий характер.

Рисунок 6.16. Пространственное распределение плотности в момент времени t=0.501; -

точное решение, - приближённое решение (схема метода WAF, h=0.02).

________________________________________________________________________________

Флуктуации приближённого решения в методе WAF не только ухудшают качество этого решения, но могут приводить к более серьёзным последствиям. Например, на каком-то этапе вычислений может возникнуть такая комбинация газодинамических величин, при

110