Разностные схемы

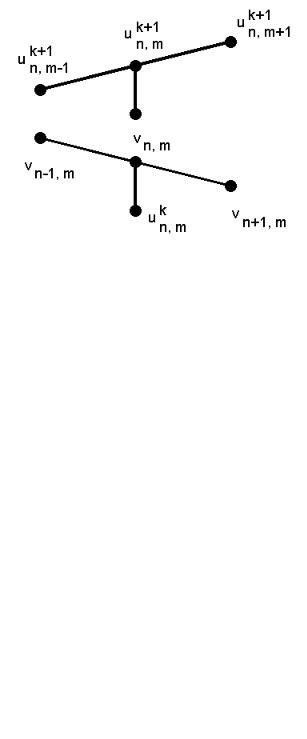
Рисунок 11.13. Шаблон для схемы (11.43).

Если γ>0, то схема (11.26) неявная; для каждого значения k необходимо решать разностное уравнение вида

uk+1	+ κγτ(	x	uk+1	+	y	uk+1) = d	n,m
n,m			n,m			n,m

относительно неизвестных значений в момент времени tk+1. Эффективное решение такого уравнения возможно только для довольно узкого класса задач (смотри параграф 11.3). С другой стороны, явная схема (11.43) имеет довольно сильное ограничение на шаг по времени (для квадратной сетки β≤1/4), что также может потребовать большого объёма вычислений. Поэтому мы не будем останавливаться на подробном анализе этой схемы, а перейдём к рассмотрению более экономичных разностных схем построенных на основе метода расщепления.

Существуют различные способы построения разностных схем, основанных на уравнениях (11.40) и (11.41). Мы рассмотрим лишь несколько примеров. Если использовать явную схему (11.20) для решения задач (11.40) и (11.41), то получим явную схему расщепления

v

n,m

−uk

n,m

= κ

uk

+ f

(x

,y

,t

) ,

x

n

m

τ

n,m

s

k

n=1, …, N-1; m=ms, …, me,

(11.44)

uk+1 −v

n,m τ n,m = κ yvn,m ,

n=ns, …, ne; m=1, …, M-1, un0,m = g(xn ,ym ),

+ разностная форма граничных условий,

31

которая представляется в виде шаблона, показанного на рис 11.14.

	Рисунок 11.14. Шаблон для схемы (11.44).
При записи этой схемы мы ввели обозначения wk		≡ v	n,m	и wk+1	≡ uk+1			. Параметры n , n ,
	n,m			n,m	n,m						s e
ms, me зависят от типа граничных условий:
	1 , для граничных условий 1-го рода при x =					0
ns							,
	=	2-го рода при x =				0
	0 , для граничных условий
	N −1 , для граничных условий 1-го рода при x = l								x
											,
n =
e					= lx
	N , для граничных условий 2-го рода при x
	1 , для граничных условий 1-го рода при y =					0
ms							,
	=	2-го рода при y =				0
	0 , для граничных условий
	M −1 , для граничных условий 1-го рода при y = l									y
											.
m =
e					= ly
	M , для граничных условий 2-го рода при y

Вычисления по схеме (11.44) производятся следующим образом. На первом шаге, при каждом значении m, решаются одномерные задачи по x, что даёт промежуточное решение v={vn,m}. Затем, решая, при каждом значении n, одномерные задачи по y, мы получаем сеточную функцию uk+1, которая и считается приближённым решением в момент времени

tk+1.

Для анализа аппроксимации запишем сначала схему (11.44) в виде одного уравнения. Для этого выразим vn,m из первого уравнения и подставим это выражение во второе уравнение. В результате получим

32

unk,+m1 −unk,m

= κ(

xunk,m + yunk,m )+

τ

(11.45)

τκ2

+

τ

) + f (x

uk

f (x

n

,y

m

,t

n

,y

m

,t

k

).

y x

n,m

y s

k

s

Подставляя в это выражение точное решение,

и учитывая,

что операторы xun,m и yun,m

аппроксимируют вторые производные по x и y (смотри (11.11)), приходим к

дифференциальному приближению в точке (xn, ym, tk)

∂u

(x

,y

,t ) +

1 τ

∂2u

(x

,y

,t ) +O(τ2 ) =

∂t

n

m

k

2

∂t2

n

m

k

2

2

κ

∂ u

(xn ,ym ,tk ) +

∂ u

+ fs (xn ,ym ,tk ) +

2

2 (xn ,ym ,tk )

∂x

∂y

κh

2

4

u

4

2

4

∂

∂ u

τκ

∂ u

4

(xn ,ym ,tk ) +

4

(xn ,ym ,tk ) +

(xn ,ym ,tk ) +

2 2

∂x

∂y

∂x ∂y

12

τ∂2 fs (xn ,ym ,tk ) +O(h4 ).

∂y2

Поэтому схема (11.44) аппроксимирует дифференциальную задачу (11.42) с первым порядком по τ и со вторым порядком по h.

Процедура исследования устойчивости схемы (11.44) аналогична процедуре, которую мы использовали для анализа одномерных задач. Только в двумерном случае мы зададим

решение в виде
unk,m = λk exp(iα1n + iα2m).	(11.46)

Подставим это решение в (11.45) и получим (функция fs(…) при этом не учитывается, так как она не влияет на устойчивость):

λ −1	= −	4κ sin2	(	1	α1 )−	4κ sin2	(	1	α2 )+	16κ2τ2	sin2 (	1	α1 )sin2 (	1	α2 ).
τ				2				2		h4		2		2
		h2				h2

Решение этого уравнения относительно λ даёт выражение для собственного значения

оператора перехода на один шаг по времени:

λ(α1, α2 ) = (1 −4β sin2 (12 α1 ))(1 −4β sin2 (21 α2 )),

β =	κτ	,
		,
	h2

0≤α1,α2≤2π,

Поэтому

0 ≤ λ(α1, α2 ) ≤(1 −4β)2

33

и для выполнения критерия фон Неймана необходимо |1-4β|≤1, откуда следует условие устойчивости β≤1/2. Это говорит о том, что мы можем выбрать вдвое больший шаг по времени по сравнению с явной схемой (11.43).

Если мы используем для решения задач (11.40) и (11.41) неявную схему (11.21) с γ=1, то получим неявную схему расщепления

v −uk

n,m τ n,m = κ xvn,m + fs (xn ,ym ,tk ),

n=1, …, N-1; m=ms, …, me,

(11.47)

uk+1	−v	n,m
n,m			= κ	yunk,+m1 ,
	τ

n=ns, …, ne; m=1, …, M-1, un0,m = g(xn ,ym ),

+ разностная форма граничных условий,

которая представляется в виде шаблона, показанного на рис. 11.15.

Для последовательного вычисления решения по схеме (11.47) на первом шаге, при

каждом значении m, решаются системы уравнений вида (11.28), где

w = (v0,m ,...,vN ,m )T , d = (u0,k m + τfs (x0,ym ,tk ),...,uNk ,m + τfs (xN ,ym ,tk ))T .

Затем, при каждом значении n, решаются системы уравнений вида (11.28), где

w= (unk,0+1,...,unk,+M1 )T , d = (vn,0,...,vn,M )T .

Врезультате мы получаем требуемое решение в момент времени tk+1.

34

Рисунок 11.15. Шаблон для схемы (11.47).

Для нахождения порядка аппроксимации выразим vn,m из второго уравнения и подставим результат в первое уравнение. Это даёт следующее разностное уравнение:

unk,+m1 −unk,m

= κ( xunk,+m1 + yunk,+m1 )+

τ

.

(11.48)

uk+1

+ f

τκ2

x

(x

n

,y

m

,t

).

y

n,m

s

k

Анализ этого уравнения показывает, что схема расщепления (11.47) аппроксимирует дифференциальную задачу (11.42) с точностью до членов O(τ+h2). Подстановка решения (11.46) в уравнение (11.48) даёт следующее выражение для собственных значений оператора перехода:

λ(α1, α2 ) =						1					.
	1	+ 4β sin2	(	1	α )	1	+ 4β sin2	(	1	α )
				2					2
(					1 )(					2 )

Тогда |λ(α1,α2)|≤1 для всех значений α1,α2 и значит схема (11.47) устойчива при любых значениях β>0.

Вообще говоря, рассмотренный нами способ расщепления не является единственно возможным. Например, уравнение (11.38) можно представить в следующей форме

∂u			2			2					2			2
	=	κ	∂ u		+	∂ u			+	κ	∂ u		+	∂ u
				2			2					2			2	.
∂t			∂x			∂y					∂x			∂y
		2								2

На основе такого расщепления можно записать следующую схему:

	vn,m −unk,m		κ		k	1
		=		( xvn,m +	yun,m )+		fs (xn ,ym ,tk ) ,	(11.49)
	τ		2			2

n=1, …, N-1; m=ms, …, me,

	unk,+m1 −vn,m		κ		k+1	1
		=		( xvn,m +	yun,m )+		fs (xn ,ym ,tk ),
	τ		2			2

n=ns, …, ne; m=1, …, M-1, un0,m = g(xn ,ym ),

+ разностная форма граничных условий, которая имеет шаблон, показанный на рис. 11.16.

35

Рисунок 11.16. Шаблон для схемы (11.49).

Эта схема получила название метод переменных направлений (ADI, Alternating Direction Implicit). Так как эта схема является неявной, то процедура расчёта по этой схеме аналогична процедуре расчёта по неявной схеме расщепления (11.49). Более подробная запись, анализ аппроксимации и устойчивости схемы (11.49) оставляется читателю в качестве упражнения.

В заключении, обсудим расчёт граничных условий. Разностная форма граничных условий первого рода практически одинакова для всех рассмотренных нами схем. Например, условие u(0,y,t)=f(y,t) в случае явной схемы (11.26) записывается как

uk+1	= f (y	,t	k+1	) , m = 1,...,M −1.
0,m	m

Вслучае схем расщепления (11.44) и (11.48) граничное условие имеет вид

v0,m = f (ym ,tk+1) , m = 1,...,M −1 .

и, так как на втором шаге расчёта по этим схемам это значение не изменяется, то можно положить u0,k+m1 = v0,m . В случае граничных условий второго рода, их разностная форма зависит от вида основной разностной схемы. В качестве примера рассмотрим граничное условие

a ∂∂ux (0,y,t) = f (y,t) .

Для явной схемы (11.43) применение метода фиктивных областей даёт следующую разностную форму этого граничного условия

36

uk+1 = (1 −2β)uk + 2βuk + β(uk + −2uk + uk − )+

0, 0, 1, 0, 1 0, 0, 1 m

m

m

m

m

m

2βh f (y		,t ) + τf (x			,y		,
	m			0		m	,t ),
a		k	s				k

m=1, …, M-1.

Представление граничных условий для схем расщепления (11.44) и (11.47) непосредственно следует из выражения (11.26). Поэтому для схемы (11.44) можно записать

v0,m = (1 −2β)u0,k m + 2βu1,km + 2βah f (ym ,tk ) + τfs (x0,ym ,tk ), m=ms, …, me.

Аналогично, для схемы (11.47) получим

(1 + 2β)v0,m −2βv1,m = u0,k m + 2βah f (ym ,tk ) + τfs (x0,ym ,tk ), m=ms, …, me.

________________________________________________________________________________

Пример 11.3 (нагрев пластины при воздействии на неё теплового потока)

Рассмотрим квадратную пластину размером l и толщиной d. Пусть при z=0 она теплоизолирована, а при z=d на неё воздействует распределённый тепловой поток вида g(x,y,t)=16f0(x/l)(1-x/l)(y/l)(1-y/l)exp(-ct). В начальный момент времени t=0 пластина имеет температуру u0. Края пластины теплоизолированы. Тогда распределение температуры

в пластине подчиняется уравнению (11.25) с fs(x,y,t)=g(x,y,t) и условиям u(x,y, 0) = u0 ,

∂u	(0,y,t) =	∂u	(l,y,t) = 0 ,	(11.50)
∂x		∂x

∂∂uy (x, 0,t) = ∂∂uy (x,l,t) = 0 .

Здесь под u(x,y,t) понимается средняя по толщине пластины температура.

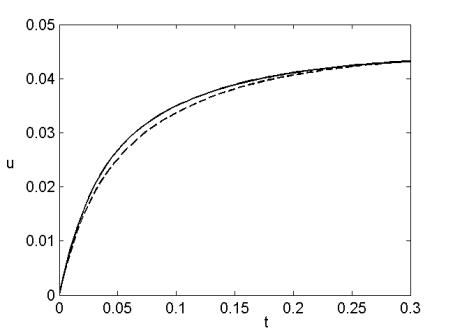
На рисунке 11.11 показана зависимость температуры в центре пластины от времени, при κ=1, l=1, f0=1, c=10 и u0=0. Точное решение этой задачи имеет вид

u(x,y,t) = f0 ∑∑∞ ∞ Un,m γn,m (t)sin πmyl sin πnxl ,

n=0 m=0

где

37

		4 / 9 , n = m = 0
				16
		−		2			2 (1 + cos(πm)) , n = 0,m ≠ 0
				3π m
U								,
	n,m	=		16
								(1 + cos(πn)) , n ≠ 0,m = 0
		−
				2		2
				3π n
				64
							(1 + cos(πn))(1 + cos(πm)) , n ≠ 0,m ≠ 0
			4 2		2
			π n m

γn,m (t) =	exp(−bn,mt)−exp(−ct)			κπ2	(n	2	2	).
			, bn,m =	l2			+ m
	c −b
	n,m

Приближённое решение вычисляется с помощью явной схемы расщепления (11.44).

Рисунок 11.11. Решение уравнения (11.42) с условиями (11.50) ; - точное решение,

- приближённое решение (h=0.1, τ=0.005).

________________________________________________________________________________

11.3.Распространение акустических волн

Вэтой главе мы обсудим численные методы решения задач распространения волн малой амплитуды. Необходимость решения таких задач возникает в самых различных областях, например:

1) аэроакустика (снижение шума)

2) распространение электромагнитных волн (микроэлектроника)

3) волны в твёрдых телах (методы неразрушающего контроля, динамика конструкций,

сейсморазведка)

38

4)методы медицинской диагностики

5)предсказание прихода волны цунами

Мы начнём наше обсуждение с простейшего уравнения колебаний.

11.3.1.Разностная схема для уравнения колебаний.

Водномерном случае, колебания однородной среды в отсутствии внешнего

воздействия описываются уравнением
∂2u = c2		∂2u		,	(11.51)
∂t2		∂x2
0 ≤ x ≤ l, 0 ≤ t ≤ T,
с начальными условиями
u(x,0) = g1(x) ,	∂u (x,0) = g2 (x) ,
		∂t
и граничными условиями
	∂u				= f1(t) ,
α1u(0,t) + α2 ∂x			(0,t)
α3u(l,t) + α4	∂u		(l,t) = f2 (t) .
	∂x

Здесь u обозначает либо скорость частиц среды, либо давление и c – скорость звука. Введём разностную сетку с шагами τ и h=l/(N-1), где N – количество узлов разностной сетки. Используем разностное выражение для второй производной и применим его для аппроксимации производной по времени в точке xn и производной по пространству в момент времени tk. В результате получим разностную схему

uk+1	−2uk	+ uk−1	= c2	uk	−2uk	+ uk
n	n	n		n+1	n	n−1	,	(11.52)
					h2
	τ2

n=1, …, N-1; k=1, 2, … ,

которая приводит к вычислительной формуле

uk+1 = 2uk −uk−1 + r2(uk+ −2uk + uk− ),

n n n n 1 n n 1

n=1, …, N-1; k=1, 2, … ,

где r=cτ/h – безразмерный параметр, называемый параметром Куранта. Шаблон для схемы (11.52) показан на рис. 11.12, поэтому её часто называют схемой «крест».

39

Рисунок 11.12. Шаблон схемы «крест».

Значения приближённого решения при k=0 и k=1 вычисляются из начальных условий, а значения при n=0 и n=N вычисляются из граничных условий. В случае граничных

условий первого рода (α2=α4=0,α1=α3=1) формулы имеют простой вид: u0k = f1(tk ) , uNk = f2(tk ),

k=1, 2, … .

Для аппроксимации граничных условий второго рода (α2=α4=1,α1=α3=0) следует использовать метод фиктивных областей. Рассмотрим эту процедуру на примере граничного условия заданного в точке x=0. Введём фиктивный слой с координатами (x-1,tk), тогда можно аппроксимировать производную в граничной точке со вторым порядком по h, используя центральную разность

uk −uk

1 2h −1 = f (tk ),

k=1, 2, ….

В дополнение, запишем схему (11.2) при n=0

uk+1	−2uk	+ uk−1	= c2	uk −2uk		+ uk
0	0	0		1	0	−1	,
	τ2				h2

k=1, 2, … .

Исключая фиктивное значение из последнего выражения, мы получим формулу для вычисления приближённого решения в граничной точке

40