Разностные схемы

ГЛАВА 11

Численные методы решения задач математической физики

Математические модели различных физических явлений часто формулируются в виде краевых задач для дифференциальных уравнений в частных производных, и изучение таких моделей требует решения этих уравнений. Мы рассмотрим методы, основанные на конечных разностях. Основная идея этих методов состоит в том, что приближённое решение определяется на некотором множестве точек, обычно называемом сеткой. Для вычисления этого приближенного решения используются конечноразностные уравнения, которые приближают и заменяют дифференциальное уравнение.

11.1. Основные методы построения и анализа разностных схем

11.1.1. Обсуждение основных понятий на примере уравнения переноса.

Рассмотрим основные идеи на примере численного решения задачи Коши для уравнения переноса. Если u(x,t) обозначает амплитуду малого возмущения в точке x в момент времени t, то распространение этого возмущения в бесконечной среде описывается следующим уравнением:

	∂u	+ c	∂u	= 0 , -∞ ≤ x ≤ ∞, t ≥ 0,	(11.1)
	∂t		∂x

u(x, 0) = g(x), -∞ ≤ x ≤ ∞,

где c=const – скорость волны, которую для определённости мы будем считать положительной. Эта задача является линейной и имеет решение u(x,t)=g(x-ct), t>0, то есть начальное состояние просто смещается вправо со скоростью c. Предположим, что функция g(x) равна нулю при x≤0 и мы будем рассматривать решение при x>0.

Вначале мы должны задать разностную сетку. Для одномерных нестационарных уравнений она определяется узлами (xn,tk) как показано на рисунке 11.1, где xn=nh, n=0,1,… и tk=kτ, k=0,1,…. Параметры h=xn+1-xn и τ=tk+1-tk называются соответственно шагами по пространству и времени.

1

Рисунок 11.1. Разностная сетка на плоскости (x,t).

Приближённое решение уравнения (11.1) определяется в узлах сетки, то есть оно

представляет собой множество значений

uk = {unk = u(a)(xn ,tk )} , n=0,1,…; k=0,1,… .

Такое множество часто называют сеточной функцией. Теперь нам нужно заменить производные некоторыми разностными операторами, определёнными на сетке. Такие операторы были введены в главе 7. Применяя разность вперёд для приближения производной по времени в точке xn и разность назад для приближения производной по пространству в момент времени tk, мы получим, вместо дифференциального уравнения (11.1), разностное уравнение в каждом узле сетки:

uk+1 −uk		uk	−uk
n	n + c	n	n−1	= 0 , n=0, 1, …; k=0, 1, …	(11.2)
			h
	τ

un0 = g(xn ), n=0, 1, ….

Набор разностных уравнений определённых на некоторой сетке называется конечноразностной схемой (или просто разностной схемой). Для вычисления приближённого решения, перепишем разностную схему (11.2) в виде

unk+1 = unk	−cτ	(unk	−unk−1) , n=0, 1, …; k=0, 1, …	(11.3)
	h
un0	= g(xn ), n=0, 1, ….

2

Из начального условия u(x,0)=g(x) следует, что значения un0 = g(xn ), известны для каждого n=0,1,…. Поэтому, из формулы (11.3) можно вычислить значения un1 для каждого n=0,1,… . Повторяя эту процедуру, после того как значение u1 определено, можно последовательно вычислить значения u2, u3, …. Разностные схемы, которые позволяют непосредственно вычислять решение в момент времени tk+1 через известное решение в момент времени tk, называются явными (схема (11.2) является примером такой схемы).

Вообще говоря, можно построить бесконечное количество разностных схем для данного дифференциального уравнения. Например, модифицируем схему (11.2), приближая производную по пространству не в момент времени tk, а в момент времени tk+1. В результате мы получим следующую разностную схему для уравнения (11.1):

uk+1 −uk		+ c	uk+1 −uk+1		= 0 , n=0, 1, …; k=0, 1, …	(11.4)
n	n		n	n−1
	τ			h
	un0	= g(xn ), n=0, 1, ….

Это выражение является примером неявной схемы. В общем случае, такие схемы не позволяют непосредственно вычислить решение в момент времени tk+1 через известное решение в момент времени tk, так как они образуют некоторую систему уравнений (для данной задачи мы предположили, что g(x)=0 при x≤0, поэтому unk−+11 = 0 и вычисления могут быть организованы явным образом). Применяя разность вперёд для приближения

производной по пространству в момент времени tk, мы получим ещё одну схему:
uk+1 −uk		+ c	uk	−uk	= 0 , n=0, 1, …; k=0,1,…	(11.5)
n	n		n+1	n
				h
	τ

un0 = g(xn ), n=0, 1, ….

Естественно, что все эти схемы имеют разные свойства. Эти различия показаны на рисунках 11.2-11.4, которые представляют результаты вычислений для разностных схем (11.2), (11.4) и (11.5), вместе с точным решением уравнения (11.1) u(x,t)=g(x-ct) при c=1 и

0 , x < 0

g(x) = x(2 −x) , 0 ≤ x ≤ 2 .

0 , x > 2

3

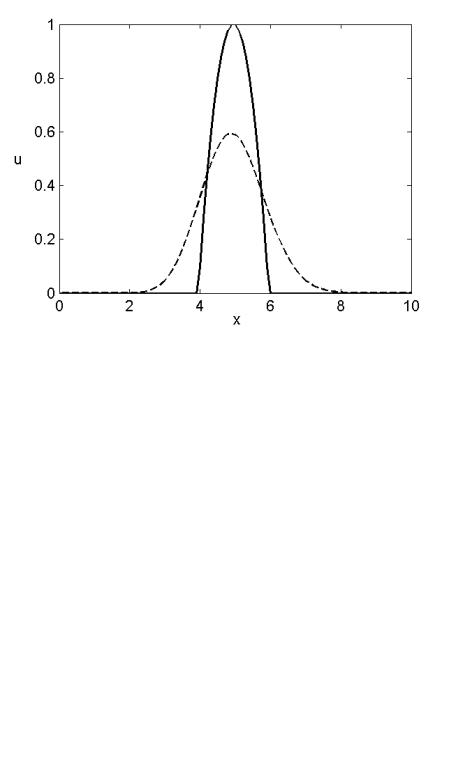
Рисунок 11.2 Решение задачи (11.1); - точное решение , - приближённое решение (разностная схема (11.2), t=4, h=0.1, τ=0.05).

Рисунок 11.3 Решение задачи (11.1); - точное решение , - приближённое решение (разностная схема (11.4), t=4, h=0.1, τ=0.05).

4

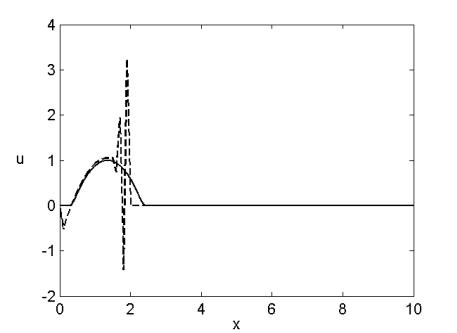
Рисунок 11.4 Решение задачи (11.1); - точное решение , - приближённое решение (разностная схема (11.5), t=0.4, h=0.1, τ=0.05).

Сравнение результатов показывает, что при вычислении по схеме (11.5) погрешность быстро накапливается и после небольшого числа шагов увеличивается до неприемлемой величины. Это явление называется неустойчивостью, и оно является внутренним свойством самой системы разностных уравнений (11.5).

Этот пример демонстрирует, что построение разностных схем и решение дифференциальных уравнений с помощью этих схем не совсем простая задача. Часто возникают ситуации когда, казалось бы, схема должна давать достоверный результат, а мы получаем приближённое решение, которое не имеет ничего общего с точным решением. Поэтому, прежде чем рассматривать методы построения разностных схем, мы должны познакомиться с требованиями, выполнение которых обязательно для любой практически пригодной схемы.

Основные свойства, которым должна удовлетворять разностная схема есть свойства аппроксимации и устойчивости. Определения этих свойств были приведены в главе 7. Здесь мы кратко рассмотрим анализ аппроксимации и устойчивости разностных схем для уравнений математической физики на примере разностных схем для задачи (11.1).

5

Разностную схему можно записать в символическом виде Dhu=f. Если подставить точное решение задачи u(e) = {u(xn ,tk )} в разностную схему, то мы не получим точного равенства, то есть возникает некоторый вектор невязки:

Dhu(e)=f+δf.

Мы будем говорить, что разностная схема аппроксимирует дифференциальную задачу на решении u(x,t) если ||δf||→0 когда h→0 и τ→0. В дополнение, если выполняется неравенство

||δf||≤C1hp+C2τq,

(11.6)

где константы C1>0, C2>0, p>0, q>0, тогда мы будем говорить, что имеет место аппроксимация порядка p по h и порядка q по τ.

Рассмотрим возмущённую разностную схему
Dhz=f+ε,	(11.7)

которая получается из разностной схемы путём добавления в правую часть возмущения ε. Мы будем называть разностную схему устойчивой, если существуют числа τ0>0 и δ>0, такие что для любого τ<τ0 и ||ε||<δ разностная задача (11.7) имеет единственное решение z и это решение отличается от u на сеточную функцию z u, которая удовлетворяет оценке ||z- u||≤C||ε||, где константа C не зависит от h и τ. Это неравенство означает, что малое возмущение правой части разностной схемы приводит к малому возмущению решения. В случае линейной дифференциальной задачи, следующее определение эквивалентно данному выше определению. Мы будем называть разностную схему устойчивой, если для любой правой части f разностная задача Dhu=f имеет единственное решение u и выполняется

оценка
||u||≤C||f||,	(11.8)

где константа C не зависит от h и τ.

Основной вопрос, который возникает при практических вычислениях - насколько полученное приближённое решение отличается от точного решения и как сделать это отклонение достаточно малым. Предположим, что разностная схема аппроксимирует задачу на решении u(x,t) и устойчива. Тогда приближённое решение u сходится к точному решению u(e), то есть ||u(e)-u||→0 когда h→0 и τ→0. Если при этом выполняется неравенство (11.6), то в этом случае мы будем говорить, что имеет место сходимость порядка O(hp+τq) или, что разностная схема (11.8) имеет точность порядка p по h и порядка q по τ. Понятно, что чем

6

больше значения p и q (выше порядок аппроксимации), тем быстрее приближённое решение стремится к точному решению по мере уменьшения шагов сетки. Однако, сравнение схем по порядку точности имеет смысл проводить лишь при достаточно малых шагах расчётной сетки h и τ , при этом главный член ошибки аппроксимации зависит не только от шагов сетки, но и от производных решения (смотри параграф 11.1.2). Практически же используются достаточно крупные расчётные сетки, на которых асимптотические оценки могут быть несостоятельны. Таким образом, может оказаться, что схема первого порядка точности на реальных сетках точнее схемы второго порядка точности и т. д. Наличие сходимости является основным требованием, предъявляемым к разностным схемам, так как только в этом случае мы можем аппроксимировать точное решение u(e) с любой точностью, в пределах машинной арифметики, выбирая шаги по пространству и времени достаточно малыми.

11.1.2. Анализ аппроксимации.

Так как точное решение исходной задачи нам неизвестно, мы можем сделать только оценку невязки. Далее мы рассмотрим пример, который демонстрирует общепринятый метод исследования аппроксимации.

Рассмотрим разностную схему (11.2) для задачи (11.1). Если вместо сеточной функции u подставить точное решение u(x,t), то выражение (11.8) примет вид

	u(xn ,tk+1) −u(xn ,tk )		+ c	u(xn ,tk ) −u(xn−1,tk )	= 0 ,	(11.9)
	τ			h

n=1,2,…; k=0,1, … .

Исследуем аппроксимацию в точке (xn,tk). Предположим что все частные производные функции u(x,t), до второго порядка включительно, непрерывны и ограничены. Тогда мы можем разложить u(xn-1,tk)=u(xn-h,tk) и u(xn,tk+1)=u(xn,tk+τ) в окрестности точки (xn,tk) по степеням h и τ, используя формулу Тейлора:

u(x

−h,t

) = u(x

,t

) −h

∂u

(x

,t

) +

1 h2

∂2u

(x

,t ) +O(h3 )

∂x

n

k

n

k

n

k

2 ∂x2

n

k

и

u(x

,t

+ τ) = u(x

,t

) + τ

∂u

(x

,t

) +

1

τ2 ∂2u

(x

,t ) +O(τ3 ) .

∂t

2

n

k

n

k

n

k

∂t2

n

k

Подставляя эти разложения в (11.9), получим

7

∂u

(x

,t ) + c

∂u

(x

,t

) = −

1

τ

∂2u

(x

,t ) +

1 ch

∂2u

(x

,t ) +O(h2

+ τ2 ),

(11.10)

∂t

n

k

∂x

n

k

2

∂t2

n

k

2

∂x2

n

k

n=1,2,…; k=0,1,… .

Выражения такого вида называются дифференциальными приближениями разностного уравнения. По своей сути они занимают промежуточное место между исходным дифференциальным уравнением и аппроксимирующей его разностной схемой. Дифференциальное приближение имеет структуру дифференциального уравнения, но его коэффициенты зависят от параметров рассматриваемой схемы , что облегчает аналитическое исследование её свойств.

Выражение в правой части (11.10) представляет собой невязку, так как начальное условие задаётся точно. Оценка нормы невязки даёт

1

2

1

2

∂ u

∂ u

|| δf

|| = max max

− τ

2

(xn ,tk ) +

ch

2

(xn ,tk )

≤

k

n

2

∂t

2

∂x

1

∂

2

2

∂ u

c

u

max max

max max

τ

(x

,t

)

+ h

(x

,t )

= C h +C

τ,

k

n

2

n

k

k

n

2

n

k

1

2

2

∂t

2

∂x

то есть разностная схема (11.2), в общем случае, аппроксимирует задачу (11.1) с первым порядком по h и τ. Анализ аппроксимации иногда позволяет получить условия на параметры сетки, при которых сходимость разностной схемы значительно ускоряется. В случае разностной схемы (11.2) для задачи (11.1) такая возможность существует. Из уравнения (11.1) следует, что

∂2u

= c2

∂2u

,

∂3u

= −c3

∂3u

.

∂t2

∂x2

∂t3

∂x 3

Тогда выражение (11.10) можно записать в виде

∂u

(x

,t

) + c

∂u

(x

,t

) = −1 c(h −cτ)

∂2u

(x

,t

) −

1 c(h2

−c2τ2 )

∂3u

(x

,t )+ ... ,

∂t

∂x

∂x 3

n

k

n

k

2

∂x2

n

k

6

n

k

n=1, 2, …; k=0, 1, … .

Если мы выберем τ=h/c, то невязка равна нулю и разностная схема будет давать точное решение в пределах погрешности вычислений.

Погрешность аппроксимации разностной схемы возникает, в основном, при замене дифференциальных операторов на разностные операторы. Применяя рассмотренный выше

8

подход, получим следующие выражения для главного члена ошибки аппроксимации часто

используемых разностных отношений:

∂u

u(s

n

+ s) −u(s

)

=

(sn ) +

1

s

∂2u

(sn ) +O (( s)2 ),

n

∂s2

s

∂s

2

u(s

) −u(s

− s)

=

∂u

(sn ) −

1

s

∂2u

(sn ) +O (( s)2 ),

(11.11)

n

sn

2

∂s2

∂s

u(s

+ s) −u(s

− s)

∂u

1

∂3u

n

2 s

n

=

(sn )

+

6

(

s)2

∂s3 (sn ) +O (( s)4 ),

∂s

u(sn + s) −2u(sn ) + u(sn − s)

=

∂2u

(sn ) +

1

2 ∂4u

(sn ) +O ((

4

),

∂s

2

(

s)

∂s

4

s)

2

12

( s)

где s обозначает пространственные переменные или время и, соответственно,

s обозначает

шаг по пространству или по времени. В дальнейшем, мы будем использовать эти готовые выражения для анализа различных разностных схем. При этом мы будем подразумевать, что решение обладает достаточной гладкостью и все необходимые нам для анализа производные существуют и ограничены.

11.1.3.Критерий фон Неймана для анализа устойчивости разностных схем.

Вэтом параграфе мы рассмотрим критерий фон Неймана, который широко используется для анализа устойчивости разностных схем. Он применим для исследования устойчивости разностных схем в случае однородной задачи Коши. Вначале мы ограничимся случаем задачи с постоянными коэффициентами, а в следующем параграфе расширим наши результаты на случай переменных коэффициентов.

Выведем критерий фон Неймана на примере разностной схемы (11.2) для задачи (11.1). Для разностной схемы, записанной в виде Dhu=f (11.8) мы имеем следующий критерий

устойчивости

||u)||≤C||f||.

Учитывая, что в нашем случае

0

f = , n=1, 2, …

g(x )

n

и определяя нормы как

9

|| u ||= max(max | unk			|) , || f ||= max | g(xn ) | ,
	k	n		n
условие устойчивости примет вид
max(max | unk		|) ≤C max | g(xn ) |= C max | un0 |.
k	n		n	n

Тогда, если будет выполняться условие

max | unk	|≤C max | un0 | , k=0, 1, …	(11.12)
n	n

то приведённое выше условие также выполнится. Для анализа устойчивости выберем

un0 = exp(iωxn ) = exp(iωnh) = exp(iαn) ,

(11.13)

где α-вещественный параметр. Тогда сеточное решение, определяемое разностной схемой (11.2) имеет вид (смысл параметра λ мы обсудим ниже):

unk = λk (α)exp(iαn) , 0 ≤ α ≤ 2π ,

(11.14)

где λ(α) в общем случае комплексный параметр. Тогда условие устойчивости (11.12) принимает вид

max | unk	|=| λk (α) | max | exp(iαn) |≤C max | exp(iαn) | ,
n	n	n

k=0,1,…

и окончательно

| λ(α) |k ≤C , k=0,1,…

Это условие выполнится для любых значений k, если

| λ(α) | ≤1 , 0 ≤ α ≤ 2π ,

(11.15)

Это и есть спектральный критерий устойчивости фон Неймана. Обсудим теперь возникновение и смысл параметра λ. Запишем разностную схему (11.2) для одного шага по времени и подставим туда начальное условие вида (11.13). В результате получим

un1

−exp(iαn)

+ c

exp(iαn) −exp(iα(n −1))

= 0 .

τ

h

Выразим u1

из этого соотношения:

n

1

= exp(iαn) −

cτ

(1

−

cτ

un

−exp(−iα))exp(iαn) = 1

(1 −exp(−iα)) exp(iαn) =

h

h

.

λ(α)exp(iαn) = λ(α)un0

Таким образом, λ представляет собой собственное значение оператора перехода на один шаг по времени (в данном случае собственное значение совпадает с оператором перехода, в

10