§ 4. Комбінації

Означення. Будь-яка підмножина з k елементів даної множини, яка містіть п елементів, називається комбінацією з п елементів по k.

З одного елемента можна утворити тільки одну комбінацію. З двох елементів а і b можна утворити дві комбінації по одному елементу і тільки одну комбінацію з двох елементів.

З трьох елементів a, b, c можна утворити такі комбінації:

{a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}.

Комбінації з п елементів даної множини по k можна також розгля­дати як розміщення з п елементів по k, які відрізняються принаймні одним елементом. Виникає запитання, як визначити кількість комбінацій з n елементів по k. Число комбінацій з п по k позначається С^k_n . Доведемо, що

. (1)

Розглянемо множину, яка складається з п елементів, і комбінації, які складаються з k елементів. Всього комбінацій С^k_n. Якщо з кожної такої комбінації утворити всі можливі перестановки (їх буде Р_k = k!), то діс­танемо всі можливі розміщення з п елементів по к, тобто число А^k_n. Отже,

А^k_n = Р_k •С^k_n , (2)

звідки

Зауважимо, що за означенням покладають 0! = 1. Тому неважко помі­тити, що С¹₁=1 і Сⁿ_n = 1.

Приклад. Збори з 30 осіб вибирають трьох делегатів на конферен­цію. Скількома способами це можна зробити?

Із множини у 30 осіб треба вибрати підмножину з трьох осіб. Це можна зробити способами .

§ 5. Властивості комбінацій

Числа і т.д. зручно записати у вигляді такої трикутної таблиці:

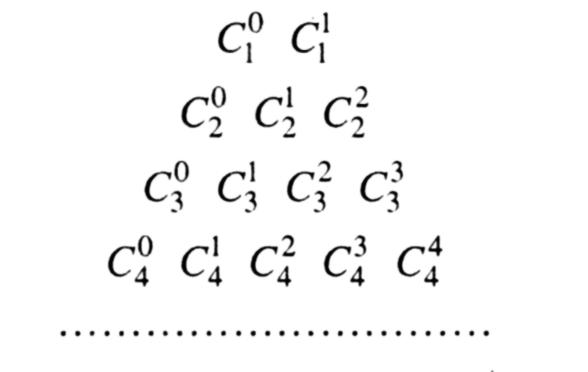
Обчисливши значення кожного символу, дістанемо

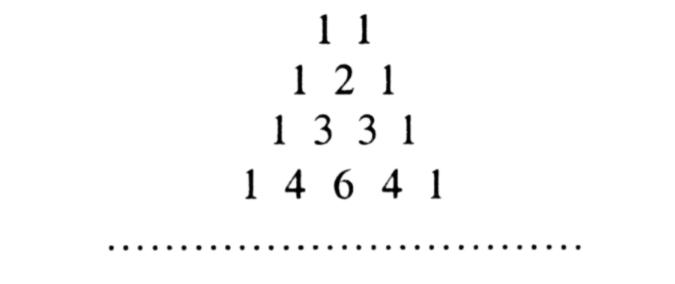
Таку таблицю називають трикутником Паскаля. На «бічних сторонах» цього трикутника стоять одиниці, а "всередині", за властивістю 2, кожне число дорівнює сумі двох чисел, що стоять над ним: 2=1+1; 3=1+2; 4=1+3; 6=3+3 і т.д. Ця властивість дає можливість виписувати послі­довно рядки трикутника Паскаля, не обчислюючи перед цим значення символів .

§ 6. Біном Ньютона

З алгебри відомо формули скороченого множення:

(a + b)² =a² +2ab + b²,

(а + b)³= а³ + 3a²b + 3ab² + b².

Коефіцієнти в правих частинах цих формул збігаються відповідно з другим і третім рядками трикутника Паскаля. Чи буде зберігатись ця закономірність для 4-го, 5-го і т.д. степеня суми?

Щоб відповісти на це запитання, розглянемо вираз (1 + х)^п , де п -натуральне число. Запишемо цей вираз як добуток співмножників:

Розкривши у правій частині дужки, дістанемо многочлен, який можна розмістити за степенями букви х. До цього многочлена ввійдуть усі степені х з показниками від 0 (вільний член) до п. Щоб записати цей многочлен, треба знайти його коефіцієнти. Нехай ціле число k задоволь­няє нерівності 0 < k < n. З'ясуємо, який коефіцієнт має степінь х^к. Цей коефіцієнт дорівнює кількості подібних членів виду х^k, які дістанемо, роз­кривши дужки. Щоб дістати х^k, беремо в k дужках другий доданок, а в інших п - k дужках перший доданок, і перемножуємо їх. Такий вибір можна здійснити С^k_п способами. Отже, розкривши дужки, матимемо С^k_п подібних членів виду х^k. Після зведення подібних членів дістанемо від­повідний член С^k_п x^k. Залишається надати k всіх можливих значень k = 0, 1, 2, ..., п, і члени додати. Таким чином, можна записати:

або, використовуючи символ суми,

Нарешті, розглянемо вираз (а + b)^п . Подамо його у вигляді

Якщо позначити =х, то за формулою (2) дістанемо

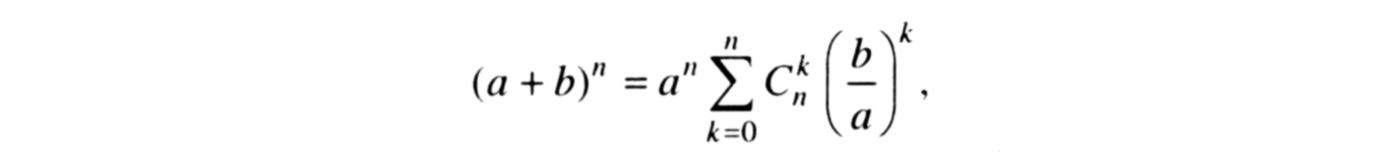
або

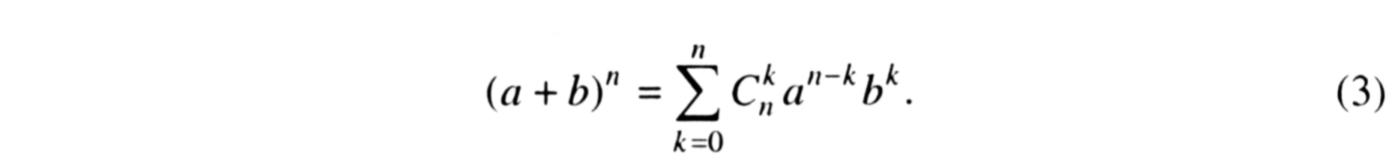
Формула (3) називається формулою бінома Ньютона.

Розгорнутий вигляд формули (3):

З формули (4) видно, що її коефіцієнти - це рядки трикутника Паскаля.

Поклавши у формулі (4) а = b = 1, дістанемо

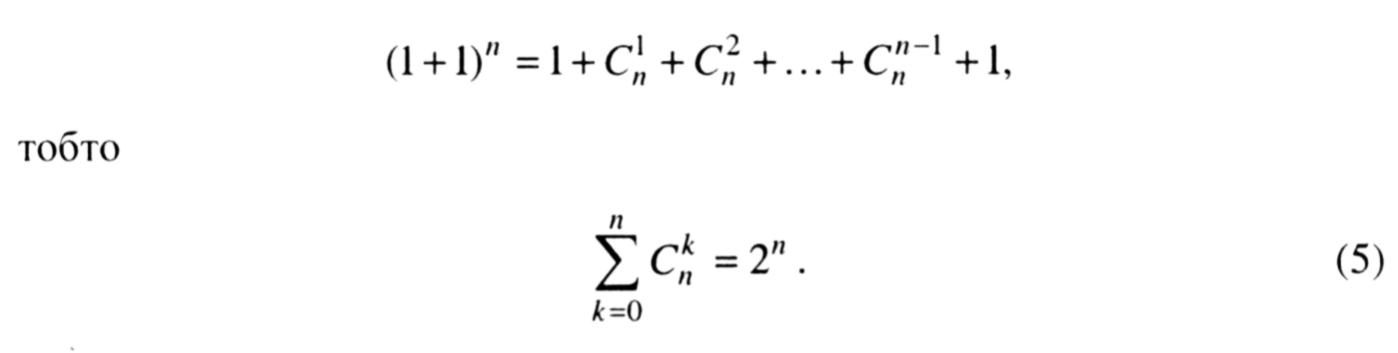
Нехай маємо скінченну множину, яка містить п елементів. Тоді кіль­кість підмножин цієї множини дорівнює 2ⁿ. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}.

ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ