Teoreticheskaya_mehanika._Kinematikastatika._Uch._metod._posobie

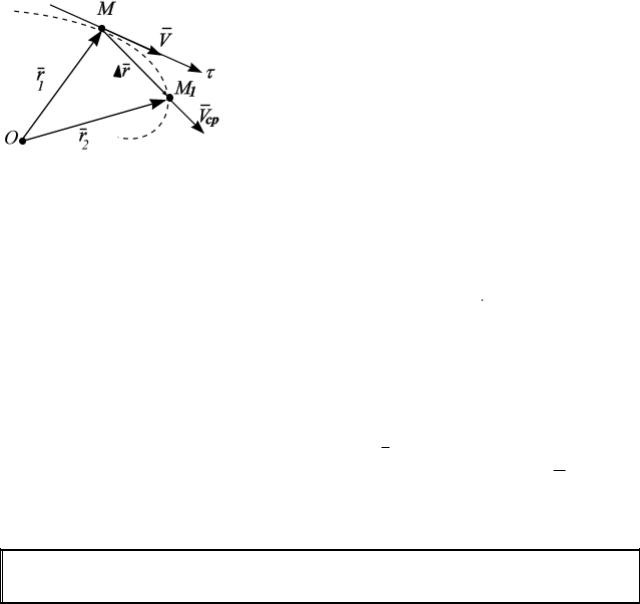
31

2.КИНЕМАТИКА

2.1.Траектория, скорость, ускорение материальной точки

Траектория точки. Геометрическое место последовательных положений движущейся точки называется ее траекторией. Если в интервале времени t1 t t2 траектория прямая линия, то движение в этом интервале называется прямолинейным, в противном случае движение называется криво-

линейным.

Скорость точки. Пусть положение дви-

жущейся точки М относительно произвольно

выбранного неподвижного центра О определя-

ется в

момент времени

t

радиус-вектором

r1 r (t) , который соединяет движущуюся точку

М с центром О (рис. 2.1).

За время

t t2 t1

радиус-вектор изме-

Рис. 2.1

нится на

r r2

r1 r (t t) r (t) .

Мгновенная скорость точки V

в момент времени t определяется как

предел средней скорости при t → 0,

т. е.

lim r

dr

r .

V

limV

cp

(2.1)

t 0

t 0 t

dt

Производная по времени от функций обозначается точкой над символом этой функции, а вторая производная – двумя точками.

Вектор скорости приложен в точке М, направлен в сторону ее движения по предельному направлению вектора r → 0, т. е. совпадает с каса-

тельной к траектории в точке М. Размерность скорости в СИ: V = дли-

на/время = м/с. Часто скорость выражают в км/ч = 0,28 м/с.

Скорость – это векторная величина, характеризующая быстроту и направление движения точки

32

Ускорение точки. Пусть движущаяся точка М в момент времени t

имеет скорость V (рис. 2.2). В момент времени t1 = t +

t эта точка занимает

положение M1 , имея скорость V1 . Чтобы изобразить приращение скорости

V

за время t, перенесем вектор скорости V1

параллельно самому себе в

точку М, тогда V

V1 V .

Ускорением точки a в момент времени t

называют предел, к которо-

му стремится среднее ускорение при t → 0, т. е.

a lim

V

dV

V

r .

(2.2)

t

dt

t 0

Вектор

ускорения a

всегда направлен

внутрь вогнутости под любым углом к касательной к траектории движения (рис. 2.2). Размерность ускорения в СИ: а = длина/время2 = м/с2.

Рис. 2.2

Ускорение – это векторная величина, характеризующая быстроту изменения модуля и направления вектора скорости.

Движение точки на плоскости

Координатный способ задания движения точки. Зададим радиус-

вектор r1 r (t) в декартовой системе координат Оху:

r (t) x A (t) i y A (t) j .

Тогда движение точки можно задать уравне-

ниями
x x(t), y y(t).	(2.3)

Рис. 2.3

t 0 .

33

Уравнения (2.3) являются уравнениями движения точки, а также уравнениями траектории точки, заданными параметрически. Уравнение траектории в системе координат Oxy будет иметь вид функции y y(x) (рис. 2.3). Для получения этой зависимости следует из уравнений (2.3) исключить параметр t . Уравнение траектории в явном виде будет иметь вид функции y y(x).

Скорость и ускорение точки по модулю и направлению вычисляются по формулам:

)

x

V

x 2 y 2 V

2

V

2

;

V

, cos(V

i

x

y

V

a a x2 y 2 ax2 a2y , cos(a i ) ax .

Содержание контрольных работ для студентов на тему «кинематика точки» дано в приложении (контрольная работа 1, задача 1).

Пример 2.1. Движение точки M по плоскости Оху задано уравнениями движения

x 2sin 2t ,	y 4cos 2t .							(а)
Значения х и у – в метрах. Построить траекторию движущейся точки,
вычислить скорость и ускорение точки в моменты времени t				и t			5	.
		1			2
			4			8

Решение. Для построения траектории движущейся точки в декартовой системе координат определим область, в которой движется точка, т. е. об-

ласть значений x(t) и y(t) .1 Так как		sin (2t)		1 и		cos(2t)		1, получаем:

1 В теории функций одной переменной эта процедура определяет область задания (существования) функций х(t) и y(t).Область определения функций в классической кинематике всегда определена –

34

2 x 2;

4 y 4.

Выделяем область, ограниченную полученными неравенствами, за эту область точка при движении не выходит (рис. 2.4) Исключим параметр t из уравнений движения (a). Для этого делим первое уравнение на 2, второе – на 4, возводим их в квадрат и складываем между собой:

	x			2	sin		2		2t
	2
				2
	y				cos			2		2t .
	4
	x			2	y		2					2	2t cos	2	2t
											sin
	2				4

Учитывая, что sin2 2t cos2 2t 1 , получим:

x		2	y			2
						1.	(б)
2				4

Траекторией движущейся точки является эллипс (рис. 2.4). Подставляя в (а) значение t 0 , находим:

x t 0 2sin(0) 0 ; y t 0 4cos(0) 4 м.

Точка в начальный момент времени занимает положение M 0 (0, 4) .

Определим направление движения точки. Уравнения движения (а) заданы возрастающей функцией x 2sin 2t и убывающей функцией y 4cos 2t , поэтому при увеличении t координата «х» возрастает, а «у» убывает, следовательно, точка движется по эллипсу по часовой стрелке.

35

Определим модуль и направление вектора скорости точки М. Имеем:

Vx x 2 2cos(2t) 4cos(2t),

Vy y 4 2sin(2t) 8sin(2t),

(в)

4cos(2t) 2 8sin(2t) 2 ,

V V 2 V 2

x

y

4cos(2t)

cos(V , x)

.

4cos(2t) 2 8sin(2t) 2

Рис.2.4

Определим модуль и направление вектора

ускорения точки М. Имеем:

ax x Vx 4 2sin(2t) 8sin 2t, ay y Vy 8 2cos(2t) 16cos(2t).

8sin 2t

a

8sin(2t) 2 16cos(2t) 2 ,

cos(a, x)

.

(г)

8sin(2t) 2 16cos(2t) 2

При t1

из (а)

получаем, что точка М имеет координаты х1

= 2,

4

у1 = 0, т. е. занимает положение (рис. 2.4) М1. Подставляя

в (в) и (г) время

t1

, получим

4

V1x 4cos 2t t 4cos(2 ) 0, V1y

8sin 2t t 8sin(2 ) 8

м

,

4

м

4

0

4

4

c

V V 2 V 2

8

cos

, x )

0; 90

,

cos(V

1

1x

1y

c

1

1

8

1

a1x 8sin 2t

8sin(2 ) 8

м

,

t

c2

4

4

a1y 16cos 2t t 16cos(2 ) 0,

4м

4

,

cos cos(a , x ) 8 1,

a

a2

a2

8

180 .

1

1x

1y

c2

1

1

8

1

36

Откладываем значение скорости (рис. 2.5, а) и ускорения (рис. 2.5, б) точки М1 на траектории.

При

t

5

из

(а)

получаем,

координаты

точки

2

8

M 2 : x2

2 1, 41 м;

y2 2

2 2,83 м .

Вычислим, используя (в) и (г), модуль и направление векторов скорости и ускорения.

а

б

Рис. 2.5

Имеем:

V2x 4cos 2t t													м	; V2 y 8sin 2t t																								м
					5		2			2																				5		4 2							;
																																						c
			8										c																	8
																													6,3					м	,
			V 2			V 2
V												8 32							40 2							10
2				2x			2 y																											c
												V2x			2
			, x) cos																	2					5			;					116,6
cos(V									2																						2
2													V2 2				10								5

для ускорения

a2x 8sin 2t			5 4						м	; a2 y 16cos 2t										8					м
							2											5					2			;
									с2																с2
		t	8														t	8
																					м	,
	a2	a2
a						32 128						160 4			10 12,6
2	2x	2 y																			c2

37

cos(a		, x) cos			a2x		4	2			5	,	2	63,4 .
	2		2
					a2		4 10				5

Откладываем значение скорости (рис. 2.5, а) и ускорения (рис. 2.5, б) точки M 2 на траектории.

Вектор скорости точки совпадает по направлению с касательной к траектории в точках M1 и M 2 , а вектор ускорения в точках M1 и M 2 направлен

во внутрь вогнутости траектории (к центру О).

Ответ: V1= 8 м/с, a1= 8 м/с2; V2= 6,3 м/с, a2= 12,6 м/с2.

Естественный способ задания движения точки.

При естественном способе задания движения точки задаются (рис. 2.6):

–траектория движения точки;

–начало и направление увеличения дуговой координаты S ;

–уравнение движения точки по траектории, как функция времени: S S(t), где S – дуговая ко-

ордината, отчитываемая от начала движения.

Рис. 2.6 Примером естественного способа задания движения является движение

поезда: траектория и направление движения определены рельсами, а уравнение движения задано таблицей – расписанием движения поезда.

Движение точки рассматривается в координатах M n . Единичный вектор направлен по вектору скорости, единичный вектор n перпендикулярен вектору , направлен по главной нормали кривой в сторону ее вогнутости

(рис. 2.6).

Скорость точки M направлена по касательной и равна

V S V .

38

Ускорение a точки M при естественном способе задания движения раскладывается на два – касательное ускорение a S V , и нормальное

ускорение a

n

S 2

n

V 2

n :

a a an .

Касательное ускорение a

характеризует изменение величины скоро-

сти, нормальное an – изменение направления вектора скорости.

Естественный способ задания движения это: S(t) + траектория

S V .

V

a a an , a S V

– касательное ускорение;

a

n

S 2

V 2

– нормальное ускорение;

tg

.

a

a a

2

a 2 ,

n

an

Связь координатного и естественного способов заданий движения точки

Рис. 2.7

Известно, что если точка движется в плоскости О xy , элемент дугиS связан с приращениями координат теоремой Пифагора (рис. 2.7):

39

S ( x) 2 ( y) 2 .

При t 0 имеем

S dS, x dx, y dx ,

тогда дифференциал дуги dS(t)

связан с дифференциалами функций dx(t) и

dy(t) (рис.2.7):

dS (dx) 2 (dy) 2 .

a

xx yy

x

2

y

2

x

2

y

2

x x(t), y t(t)

V

yx xy

,

2

2

a

x

y

an

x

2

y

2

t

t

S S0 V (t)dt S 0 Vx2 (t) V y2 (t) dt

o

o

(знак + или совпадает со знаком V , так как V Vx2 Vy2 ).

Пример 2.2.

Точка движется в плоскости Oxy . Уравнение движения точки задано

координатами x x t ,	y y t , где x и y		выражены в см, t		в с.
		t	(см);	t
Исходные данные: x 2 3cos				y 2sin	(см).
		3		6

Требуется:

1.Записать уравнение траектории в явном виде: y f x (или x f y ).

2.Построить траекторию.

3.Определить положение точки в начальный момент времени t 0 0 и мо-

мент времени t 1 1 с, направление движения точки по траектории.

4. Вычислить вектор скорости V и вектор ускорения a точки в начальный ( t 0 0 ) и конечный ( t 1 1 с) моменты времени.

40

5. Задать движение точки естественным способом (вывести закон S t ).

6. Геометрически и аналитически определить нормальную an и касательную

a составляющие ускорения точки в начальный и конечный моменты времени.

7.Найти радиус кривизны траектории в начальный и конечный моменты времени.

Решение

1.Выводим уравнение траектории в явном виде.

	3cos			t		см;
x 2
					3
		t
y 2sin					см;
		6

1			1		1 x 5;
	cos	t
	3
1			1		2 y 2.
	sin	t
	6

Из первого уравнения системы:		2sin	2
	x 2 3 1				t ; из второго
				6

	y
уравнения системы:		sin		t
	2		6

y2		2
	sin			t . Получаем:
4			6

y

2

x 2

;

3 1 2

4

x 2 31 0,5y2 ;

x 2 3 1,5y2 ;

x 1,5y2 1,

или

y

2x 2

.

3

Таким образом, получаем уравнение параболы x 1,5y2 1.

2. Строим траекторию в масштабе 1:1 (рис. 2.8).

Ветви параболы вытянуты вдоль

оси

x .

Вершина параболы: y 0;

x 1см С (−1;0).

y , см

± 1

± 2

x , см

0,5

5

3. Определяем положение точки в заданные моменты времени.