М4 дифуры

	33
ln 1 u2	ln x ln C

Или	x(1 u2 )	C C .
		1

Исключая вспомогательную функцию u (u=y/x), окончательно получаем

x(1	y2	) C ; y2	x2	C x.
	x2	1		1
		Ответ:		y2	x2	C x.
						1

ЗАДАНИЕ 3.

Найти частное решение дифференциального уравнения.

y	y ctgx	sin x,	y 0	0.
Решение.
Это	линейное уравнение			первого	порядка, т.е	уравнение вида
y	p(x) y	g(x),	p(x)	ctg(x),	q(x) sin(x) .

Решим его по методу И.Бернулли:

1.Решение дифференциального уравнения будем искать в виде произведения двух других функций, т.е. с помощью подстановки y=uv, где

u=u(x), v=v(x).	Тогда	y’=u’v+v’u.
Подставляя выражения y		и y’ в исходное уравнение, получаем:

(u 'v	v 'u)	uv ctgx	sin x.
2. Сгруппируем уравнение	относительно функции u(x)
u 'v	u(v '	v ctgx)	sin x.

3. Найдем частное решение по v так, чтобы выражение в скобках было

34

равно нулю

	v '	v ctgx 0;	dv	v ctgx;	dv	ctgx dx;	dv	ctgx dx;
			dx		v		v
	ln v	ln sin x; v	sin x.

4.Найдем общее решение по u, подставляя найденную функцию v в уравнение в пункте 2:

u 'sin x sin x; du dx; u x C.

5. Зная u и v, находим искомую функцию y: y uv (x C)sin x.

6.Решаем задачу Коши, т.е. подставляя начальные данные x=0 и y=0 в общий интеграл дифференциального уравнения, находим частный интеграл:

0 (0 C)sin 0;		С 0;
y	x sin x.
Ответ:	y	x sin x.

ЗАДАНИЕ 4.

		y			2 y		y2 x
	Найти общее решение уравнения.
					x
	Решение.
	Это уравнение Я.Бернулли, т.е уравнение вида y p(x) y yn g(x), p(x)							2	, q(x) x.
								x
	Решим его по методу И.Бернулли:
	1. Подстановка y=uv, y’=u’v+v’u.
	(u 'v v 'u)	2uv		(uv)2 x.
		x

35

2. Сгруппируем уравнение относительно функции u(x)

u 'v u(v '

2v

) (uv)2 x.

x

3. Найдем частное решение по v

так, чтобы выражение в скобках было

равно нулю

v '

2v

0;

dv

2v

;

dv

2dx

;

dv

2dx

;

v

x

x

dx

x

v

x

ln v

2ln x; v x 2

1

.

x2

4.Найдем общее решение по u, подставляя найденную функцию v в уравнение в пункте 2:

u '

u

2

(

1

)

2

x;

du

dx

;

1

ln

Cx

; u

1

.

x2

x2

u2

x

u

ln

Cx

5. Зная u и v,

находим искомую функцию y:

y uv

1

.

ln

Cx

y

1

.

Ответ:

ln

Cx

ЗАДАНИЕ 5.

Найти линию, проходящую через точку М0 для которой площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная и равная a2 .

М0 (1;9), a=3.

36

Решение.

Рис.1.

Как видно из рисунка 1, площадь указанного треугольника равна

S

1

NK

y.

2

Поскольку

tgα=y’ ( это вытекает из геометрического смысла производной),

y

y

y2

tg

y ',

NK

,

S

,

y ' 0.

NK

y '

2 y '

Таким образом, имеем дифференциальное уравнение

y2

a2 ,

y2

a2 y '.

2 y '

2

Считая y≠0 и разделяя переменные, получаем

2dy

dx

2

x

C

,

y2

a2

y

a2

y

2a2

.

Отсюда находим

Ca2

x

S

y2

a2 .

Если y’<0,

см рисунок 2,

то

2 y '

37

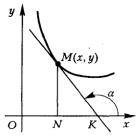Рис.2

y

2a2

.

Интегрируя это уравнение, получаем

x

Ca2

Наконец, обозначив —Ca2=С*, оба ответа объединяем в один

y

2a2

.

С *

x

Решаем задачу Коши. Если а=3, а координаты точки

М0(1;9), можно вычис-

лить константу С*:

9=18/(С*±1), С*=1

или 3.

y

18

,

y

18

.

Ответ :

1 x

3 x

ЗАДАНИЕ 6.

Найти частное решение дифференциального уравнения и вычислить значение

полученной функции при x			x0 с точностью до двух знаков после запятой.
y	1	, x 1, y 1	1, y 1 2, y 1	2.
	x	0

Решение.

38

Это задача Коши для дифференциального уравнения третьего порядка с начальными условиями. Частное решение уравнения будет иметь вид:

x

x

x

y''

(x x )2

' (x x ) y .

у

dx dx f (x)dx

0

y

2!

0

0

0

0

x0

x0

x0

Выполним трижды интегрирование функции

каждый раз в пределах от 1 до

x (x0=1).

Первое интегрирование :

x 1

dx

ln x

x

ln x.

1 x

Второе интегрирование:

1

x

u

ln x,

dv

dx

x

x

ln xdx

du

dx

,

v

x

x ln x

dx

x ln x

(x

1).

1

1

x

1

Третье интегрирование:

x

x

x

u

ln x,

dv

xdx

(x ln x (x

1))dx

(x

1)dx

x ln xdx

dx

x

2

du

,

v

1

1

1

x

2

x2

x

1

x

x

x2

1

2

x

(x 1)2

x

ln x

xdx

(x

1)dx

ln x

x

2

2

2

4

1

2

1

1

1

1

x2

1

2

1 (x 1)2

x2

3

2

1

ln x

x

ln x

x

x

.

2

4

4

2

2

4

4

Используем начальные условия

x0

1,

y0

1, y0

2,

y0

2.

x2

3

2

1

2

y

ln x

x

x

(x

1)

2(x 1)

1.

2

4

4

39

Раскрывая скобки и делая приведение подобных членов, получим

y	x2	ln x	7	x	2	5x	9	.
	2		4				4
									x2		7		2		9
							Ответ: y			ln x		x		5x		.
									2		4				4

ЗАДАНИЕ 7.

Найти общее решение дифференциального уравнения, допускающего понижение порядка.

(x 3) y y 0

Решение.

Данное уравнение 2-го порядка не содержит явно функции y. Полагая y’=p, dp

получим y и после подстановки данное уравнение обращается в dx

уравнение 1-го порядка:

(x 3) dpdx p 0.

Разделяя переменные и интегрируя, найдем

dp

dx

0; ln

p

ln

x 3

ln C; p(x 3)

C C1.

p

(x 3)

Заменяя

(x

					dy
	вспомогательную переменную p через				,	получим уравнение
		dy			dx
	3)		C1,	решая которое найдем искомый интеграл:
		dx

dy

C1dx

; y C1 ln

x 3

C2 .

(x

3)

y C1 ln

x 3

C2 .

Ответ:

40

ЗАДАНИЕ 8

Найти общее решение однородного дифференциального уравнения.

а) y 5 y 6 y 0 ; б) y ''' 6 y '' 13y 0 ;

в) y '' 4 y ' 4 y 0

Решение.

а) y 5 y 6 y 0

Заменим в этом уравнении функцию y единицей, а ее производные соответствующими степенями λ. Его характеристическое уравнение

2 5 6 0.

Корни этого уравнения λ1=6, λ2=-1 действительны и различны. Поэтому, согласно правилу 1) приложения 2, искомый общий интеграл уравнения будет y C1e6 x C2e x .

Ответ: y C1e6 x C2e x .

б) y ''' 6 y '' 13y 0

Составим характеристическое уравнение

3 6 2 13

0.

Оно имеет один действительный однократный корень λ1=0 и пару комплексных сопряженных корней λ2,3=3±2i. Согласно правилам 1) и 2) приложения 2 общий интеграл дифференциального уравнения равен

y C	e3x (C cos 2x	C sin 2x).
1	2	3

Ответ: y C1 e3x (C2 cos 2x C3 sin 2x).

41
в) y '' 4 y ' 4 y 0
Написав характеристическое уравнение	2	4 4 0, находим, что оно

имеет равные действительные корни λ1= λ2=-2.		Согласно правилу 3) прило-
жения 2, общий интеграл данного уравнения y		e 2 x (C	C x).
		1	2
Ответ: y e 2 x (C	C x).
1	2

ЗАДАНИЕ 9.

Найти частное решение линейного однородного дифференциального уравнения.

y '' 4y 5y 0, y 0

3, y 0 0.

Решение.

Найдем вначале общий интеграл данного уравнения. Его характеристиче-

ское уравнение	2	4	5 0	имеет корни		λ1,2=-2±i. Поэтому, согласно
правилу 2) приложения 2 общий интеграл y						e 2x (C1 cos x C2 sin x).
Далее, используя начальные условия, определим значения С1 и С2.
Подставляя в общий интеграл заданные значения x=0,							y=-3 ( первое началь-
ное условие), получим
		3	e0 (C cos 0 C sin 0);			3 C .
			1	2		1
Дифференцируем общий интеграл как произведение:
y ' e 2x (		2)(C cos x		C sin x)	e 2x	( C sin x	C cos x);
			1	2		1	2
	y '	e	2x ((C	2C ) cos x	(C	2C )sin x).
			2	1	1	2

42

Подставим заданные значения x=0, y’=0 ( второе начальное условие), получим второе уравнение с неизвестными С1 и С2.

0 e0 ((C	2C ) cos 0	(C	2C )sin 0);	C	2C 0.
2	1	1	2	2	1

Решим полученные уравнения как систему

C2	2C1	0,
C1	3.	С2=-6.

Подставляя значения С1 и С2 в общий интеграл, получим искомый частный интеграл данного уравнения, удовлетворяющий данным начальным условиям:

y	3e 2x (cos x 2sin x).
Ответ: y		3e 2x (cos x 2sin x).

ЗАДАНИЕ 10.

Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.

y 2 y 3y e4 x , y 0 1, y 0 0.

Решение.

1. Найдем сначала общее решение однородного уравнения, соответствующего

данному неоднородному, т.е. уравнения	y		2 y	3y	0.
Корни его характеристического уравнения		2	2	3	0 равны λ1=-1,

λ2=3, и указанное общее решение, согласно п.1) приложения 2, можно записать в виде: y C1e x C2e3x .

2.Частное решение неоднородного уравнения будем искать по форме правой части. Поскольку правая часть уравнения f (x) e4x и число γ=4 не совпа-