Тема II. Аналитическая геометрия
Основные понятия
Аналитической геометрией называется раздел математики, в котором геометрические задачи решаются алгебраическими методами. Основой аналитической геометрии является метод координат, который ввёл французский математик Рене Декарт.
Декартову систему
координат на плоскости образуют две
взаимоперпендикулярные прямые с
заданными началом отсчёта, направлениями,
единицами длины. Данные прямые называются
осями координат: горизонтальная – осью
абсцисс (обозначается
),
вертикальная – осью ординат (обозначается
).
Каждой точке плоскости ставится в
соответствие упорядоченная пара чисел
(координаты точки) и наоборот.
Напомним основные формулы аналитической геометрии, известные из школьного курса элементарной математики:
1. Расстояние между
точками
и
вычисляется по формуле
.
2. Координаты точки
,
делящей отрезок
в заданном отношении
,
вычисляются по формуле
,
.
Определение 2.1. Линия – это геометрическое место точек (ГМТ), обладающих определённым свойством. Так, например, геометрическим местом точек, равноудалённых от данной точки, является окружность; геометрическим местом точек, равноудалённых от двух данных точек, является срединный перпендикуляр.
Определение 2.2.
Уравнением линии (кривой) на плоскости
называется уравнение вида
(или
),
которому удовлетворяют координаты
и
каждой точки, лежащей на данной линии,
и не удовлетворяют координаты любой
точки, не лежащей на данной линии.
Задачи аналитической геометрии.
1. По уравнению линии построить соответствующий геометрический образ (по точкам или после проведения полного исследования).
Пример 2.1.
Построить линии, заданные уравнениями
,
,
.
2. По линии, как по геометрическому месту точек, обладающих определённым свойством, составить уравнение данной линии.
Пример 2.2.
Составить уравнение окружности, если
точки
и
являются концами её диаметра.
3. По линии, как по геометрическому образу, составить соответствующее уравнение (от графика к таблице, от таблицы к аналитической зависимости) – выходит за рамки данного курса.
4. По уравнениям двух линий найти координаты их точек пересечения.
Пример 2.3.
Найти точки пересечения линий, заданных
уравнениями
и
.
Кривые спроса и предложения.
Пусть
– цена на некоторый товар (price),
а
– количество товара, проданного по
данной цене (quantity).
Функция
(
–
demand
– спрос), которая показывает зависимость
величины спроса потребителей от цены
на товар, называется функцией спроса.
Функция
(
–
supply
– предложение), которая показывает
зависимость величины предложения
поставщиков от цены на товар, называется
функцией предложения.
p
p0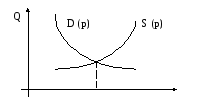
Точка пересечения
графиков данных функций называется
точкой равновесия спроса и предложения
(при фиксированном уровне дохода на
душу населения), а соответствующее
значение аргумента
– равновесной ценой. Например, равновесная
цена 10 гривен за билет в кино означает,
что при стоимости билета более 10 гривен
в зале будут пустые места (предложение
превышает спрос), менее 10 гривен – не
все желающие попадут на сеанс (спрос
превышает предложение). Ситуация, когда
спрос превышает предложение, называется
дефицитом; она возникает, если
;
в качестве ещё одного примера можно
привести периодическое исчезновение
бензина на заправках при ограничении
цены на него. Ситуация, когда предложение
превышает спрос, называется
перепроизводством; она возникает, когда
;
в качестве ещё одного примера можно
привести ситуацию со стоимостью общежития
в 2009 году, когда после резкого повышения
стоимости многие предпочитали снимать
комнаты.
Пример 2.4. Найти точку равновесия, если функции спроса и предложения заданы уравнениями
и
соответственно.
Решение.
Из соотношения
находим
,
то есть при цене 10 денежных единиц за
единицу товара спрос на данный товар
будет совпадать с его предложением.
Уравнение прямой на плоскости
Теорема 2.1.
Уравнение прямой, проходящей через
точку
на оси ординат и образующей с осью
угол
,
имеет вид
,
(2.1)
где
– угловой коэффициент прямой. Уравнение
(2.1) называется уравнением прямой с
угловым коэффициентом.
Доказательство.
Возьмём на данной прямой произвольную
точку
.
Из треугольника
по определению тангенса получим
,
или, с учётом обозначения
,
.
Замечание.
Уравнение (2.1) остаётся справедливым и
при
,
а если
,
то
и уравнение (2.1) примет вид
– уравнение прямой, параллельной оси
.
Однако с помощью уравнения (2.1) нельзя
описать прямую, перпендикулярную оси
,
поскольку в данном случае
и
не существует. Такая прямая описывается
уравнением
,
где
– абсцисса точки пересечения прямой с
осью
.
Теорема 2.2.
Уравнение прямой, проходящей через
заданную точку
и образующей с осью
угол
,
имеет вид
(2.2)
Доказательство.
Уравнение искомой прямой имеет вид
(2.1), в котором
,
– неизвестный параметр. Поскольку точка
лежит на прямой, то её координаты
удовлетворяют уравнению (2.1):
.
Вычитая данное соотношение из (2.1),
получаем уравнение (2.2).
Теорема 2.3.
Уравнение прямой, проходящей через две
заданные точки
и
,
имеет вид
.
(2.3)
Доказательство.
В предположении, что искомая прямая не
является вертикальной, её уравнение
имеет вид (2.2), в котором
– неизвестный параметр. Поскольку точка
лежит на прямой, то её координаты
удовлетворяют уравнению (2.2):
.
Подставив значение
в уравнение (2.2), получим
.
Замечание.
Если
,
то уравнение (2.3) определяет горизонтальную
прямую
;
если
,
то вертикальную прямую
.
Это непосредственно вытекает из формулы
(2.3).
Теорема 2.4.
Уравнение прямой, пересекающей оси
координат в точках
и
,
имеет вид
.
(2.4)
Доказательство.
Подставив координаты точек
и
в уравнение (2.3), получим
.
Теорема 2.5. Произвольное уравнение первой степени с двумя неизвестными
(2.5)
определяет на координатной плоскости прямую. Уравнение (2.5) называется общим уравнением прямой.
Доказательство.
Пусть
,
тогда уравнение (2.5) можно переписать в
виде
– уравнение прямой с угловым коэффициентом.
Если же
,
то обязательно
(иначе уравнение (2.5) не будет уравнением
первой степени) и
– уравнение прямой, перпендикулярной
оси
.
Теорема 2.6.
Угол
между двумя прямыми, заданными уравнениями
и
,
вычисляется по формуле
,
(2.6)
причём угол
откладывается против часовой стрелки
от положительного направления оси
.