Функция одной переменной

Определение 3.8.Функциейназывается правило, по которому каждому значению переменнойиз множестваставится в соответствие единственное значение переменной. При этомназывается независимой переменной (аргументом функции),- зависимой переменной (значением функции),- областью определения функции (обозначается).

Определение 3.9.Пусть переменнаяпринимает все значения из, тогда множествоназывается областью значения функции, а множество точек декартовой плоскости с координатами- графиком функции.

Способы задания функции

1. Аналитический – с помощью формулы , где- выражение, содержащее переменную

Пример 3.3.а),,; б),,; в),,; г),,.

2) Табличный (таблицы Брадиса, табель, расписание). Область определения должна состоять из конечного числа элементов. Применяется при проведении различных исследований, при этом важна возможность взаимоперехода между табличным и аналитическим способами задания.

3) Графический (кардиограмма). Применяется при проведении физических (или иных) опытов с помощью приборов – самописцев.

Виды функций

Определение 3.10.Функцияназывается возрастающей (убывающей, неубывающей, невозрастающей) на промежутке, еслитаких, что, имеет место неравенство(,,соответственно). Общее название таких функций – монотонные.

Определение 3.11.Пусть даны функциии, причём. Тогда функцияназывается сложной функцией (суперпозицией двух функций),- внутренней функцией,- внешней функцией.

Пример 3.4.- сложная функция, у которой- внутренняя функция,- внешняя функция.- сложная функция, у которой- внутренняя функция,- внешняя функция.

Определение 3.12.Пусть дана функция, причём каждому значениюсоответствует единственное значение. Тогда на множествеопределена функциятакая, что. Функцияназывается обратной к

Пример 3.5.Пусть, тогда, посколькуна. Обратными являются такжеипри,ипри. Графики прямой и обратной функции симметричны относительно биссектрисы первой и третьей координатных четвертей.

Определение 3.13.Основными элементарными функциями называются: степенная, показательная, логарифмическая, тригонометрические(,,), обратные тригонометрические(,,).

Определение 3.14.Элементарными функциями называются функции, получаемые из основных элементарных с помощью конечного числа алгебраических действий и суперпозиций

.

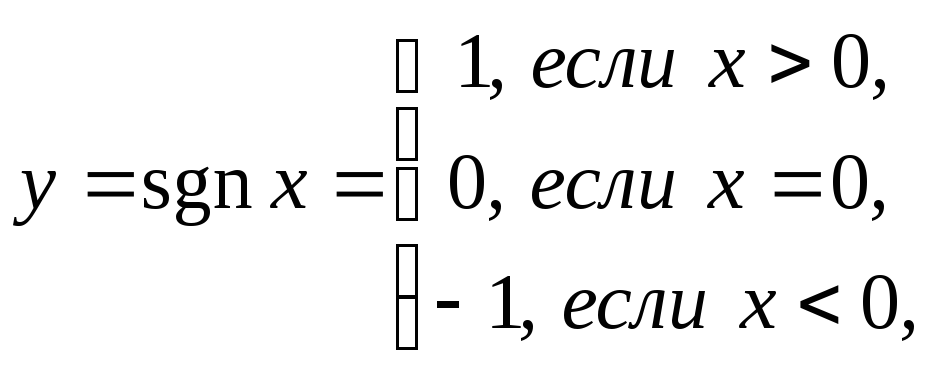
Примерами неэлементарных функций могут служить ,- целая часть числа (ставит в соответствие действительному числу наибольшее целое число, не превосходящее его:) .

Предел функции. Односторонние пределы.

Пусть функция определена в некоторой окрестности точки, за исключением, возможно, самой точки.

Определение 3.15(по Гейне).Числоназывается пределом функциив точке, если для любой последовательностиимеет место соотношение. Обозначаем

.

Число называется пределом функциина бесконечности, если для любой бесконечно большой последовательностиимеет место соотношение.

Определение 3.16 (по Коши).Числоназывается пределом функциив точке, если

(прочитать эту символьную запись словами и изобразить на координатной плоскости).

Определение 3.17.Числоназывается пределом слева функциив точке, если для любой последовательностиимеет место соотношение. Обозначаем

.

Теорема 3.7.Для существования предела функции в точке необходимо и достаточно, чтобы существовали и совпадали односторонние пределы.

Пример 3.6.Показать по определению, что.

Решение. Другими словами, необходимо в определении предела по Коши указать значение:. То есть- утверждение доказано.

Замечание.Если у функции существует предел, то для неё имеют место все свойства сходящихся последовательностей. Поэтому предел можно вычислять, применяя арифметические свойства пределов, а так же свойства бесконечно малых и бесконечно больших величин.

Пример 3.7.Найти.

Решение..

Исходя из свойств бесконечно малых и бесконечно больших величин, имеют место соотношения

(в пределе).

Если же при нахождении пределов получаются соотношения вида которые называютсянеопределённостями, необходимо провести преобразование функции.

Пример 3.8.а)====1;

б) =.

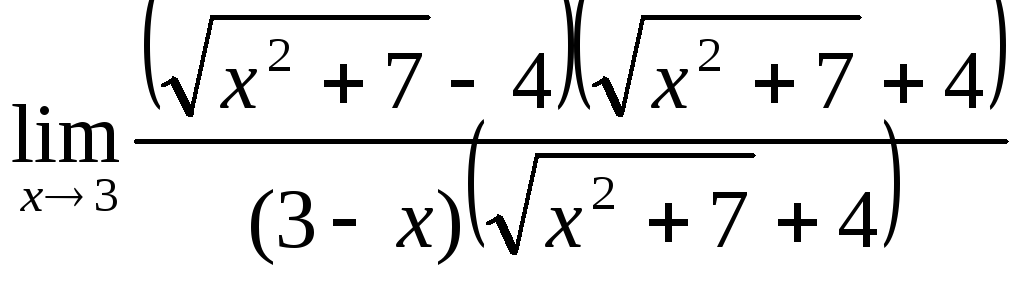
Если функция содержит тригонометрическое выражение, то для раскрытия неопределённости вида применяется «1 – ый замечательный» предел

и следствия из него

.

Пример 3.9.=

=.

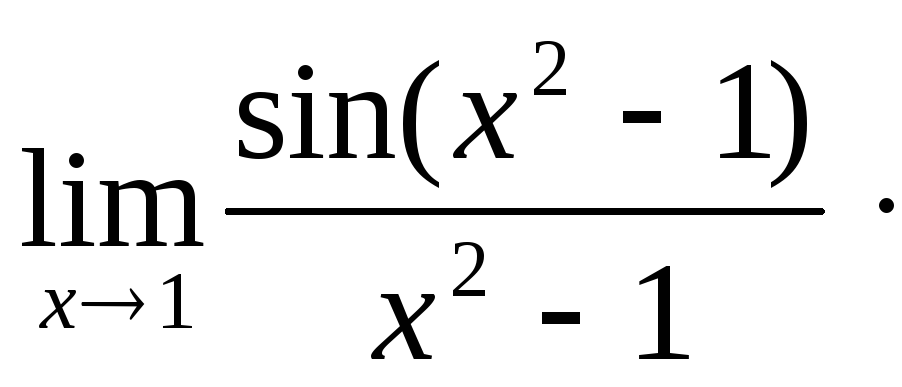
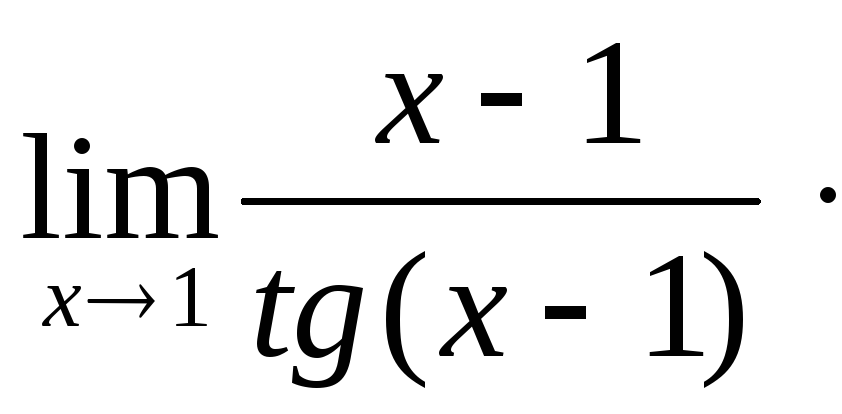
Для раскрытия неопределённостей вида применяется «2 – ой замечательный» предел

(где- число Эйлера)

или следствие из него

.

Пример 3.10.Найти.

Решение.Поскольку, а, то по следствию из «2 – го замечательного» предела получаем.

Пример 3.11.Найти==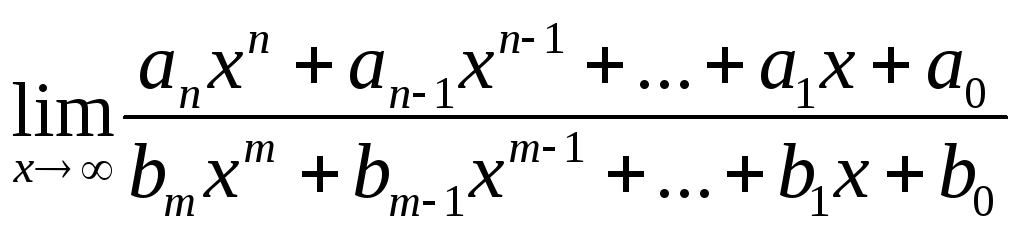

=

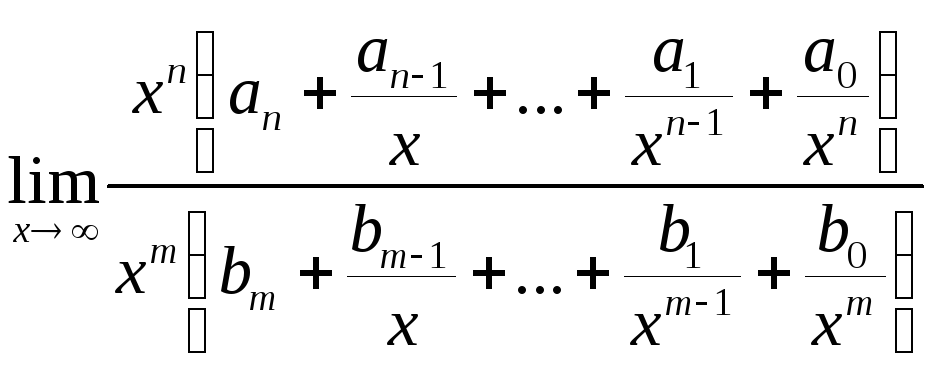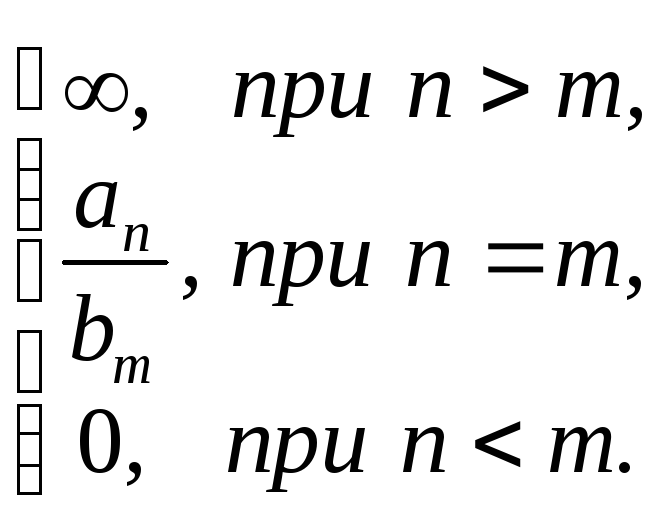
Аналогичный приём используется при нахождении предела на бесконечности для иррациональных и смешанных выражений.