Непрерывность функции

Определение 3.18.Функцияназывается непрерывной в точке, если выполняются следующие условия: 1) функция определена в точке; 2) существует конечный предел; 3) имеет место равенство.

Теорема 3.8. Элементарные функции непрерывны в каждой точке своей области определения.

Замечание.Из условия 2) непрерывности функциив точкеследует, чтоопределена в двусторонней окрестности.

Следствие 1.Функцияявляется непрерывной в точке, если выполняется предельное соотношение.

Следствие 2.Функцияявляется непрерывной в точке, если выполняется предельное соотношение.

Теорема 3.9.Пусть функцииинепрерывны в точке, тогда непрерывными в данной точке будут сумма, произведениеи частное(при условии) данных функций (справедливость данной теоремы вытекает из определения непрерывности и арифметических свойств предела функции).

С геометрической точки зрения непрерывность функции в точке означает, что график данной функции можно провести через данную точку, не отрывая карандаша от бумаги. Так, например, функция является непрерывной в точке, а функция- разрывной в точке(но непрерывной во всех остальных точках числовой прямой).

Определение 3.19.Функцияназывается разрывной в точке, если она определена в двусторонней окрестности, но при этом не выполняется хотя бы одно из условий 1) – 3) непрерывности. Точканазывается точкой разрыва функции.

Замечание.Из данного определения и теоремы 3.8 следует, что точки разрыва функции необходимо искать либо среди точек, не входящих в область определения, либо среди точек смены аналитической зависимости.

Определение 3.20.Точканазывается точкой устранимого разрыва функции, если выполняется условие 2) непрерывности функции, но при этом либо, либо.

Пример 3.12.Исследовать на непрерывность функцию.

Решение.Поскольку данная функция является элементарной, то единственно возможными точками разрыва являются точки, не входящие в область определения:. Таким образом, нам необходимо исследовать поведение функции в точке:. Так как у функции существует конечный предел в данной точке, но в самой точке функция неопределенна, то эта точка является точкой устранимого разрыва.

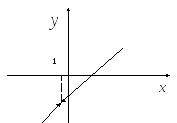
Ответ.Искомая функция является непрерывной во всех точках действительной оси, кроме точки. Данная точка является точкой устранимого разрыва.

Определение 3.21.Точканазывается точкой разрываI– го рода функции, если не выполняется условие 2) непрерывности, а именно: существуют конечные, но не равные между собой односторонние пределы:.

Пример 3.13.Исследовать на непрерывность функцию.

Решение.Перепишем исходную функцию в видеЕдинственно возможной точкой разрыва является точка, в которой функция не определена. Найдём односторонние пределы:,. Поскольку они конечные, но не равные между собой, то точкаявляется точкой разрываI– го рода.

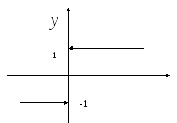
Ответ.Искомая функция является непрерывной во всех точках действительной оси, кроме точки. Данная точка является точкой разрываI– го рода.

Определение 3.22.Точканазывается точкой разрываII– го рода функции, если не выполняется условие 2) непрерывности, а именно: хотя бы один из односторонних пределов равен бесконечности или не существует.

Пример 3.14.Исследовать на непрерывность функцию.

Решение.Поскольку данная функция является элементарной, то единственно возможными точками разрыва являются точки, не входящие в область определения:. Таким образом, нам необходимо исследовать поведение функции в точке:– этого достаточно для того, чтобы данная точка была точкой разрываII– го рода.

Ответ.Искомая функция является непрерывной во всех точках действительной оси, кроме точки. Данная точка является точкой разрываII– го рода.

Определение 3.23.Точки разрываI– го иII– го рода называются точками неустранимого разрыва. Таким образом, при классификации точек разрыва определяющим является условие 2) непрерывности.

Пример 3.15.Для функции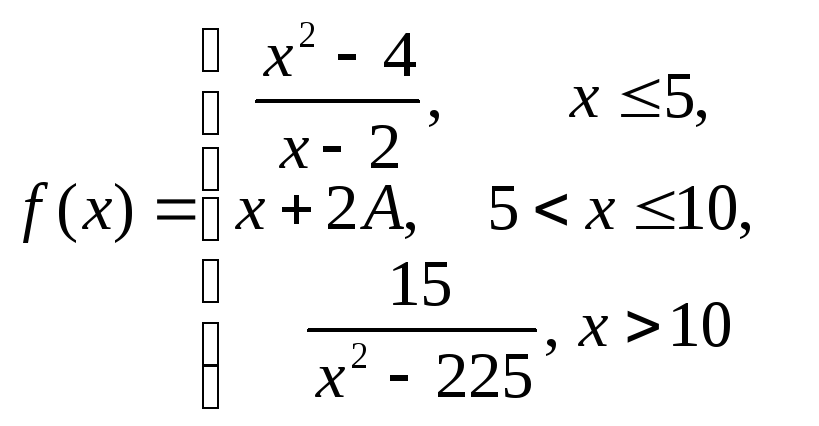необходимо: 1) найти значение параметраиз условия непрерывности функции в точке; 2) исследовать полученную функцию на непрерывность.

Решение.1) Воспользуемся определением 3.18 непрерывности: поскольку,и, то из равенстванаходим. Перепишем исходную функцию в виде

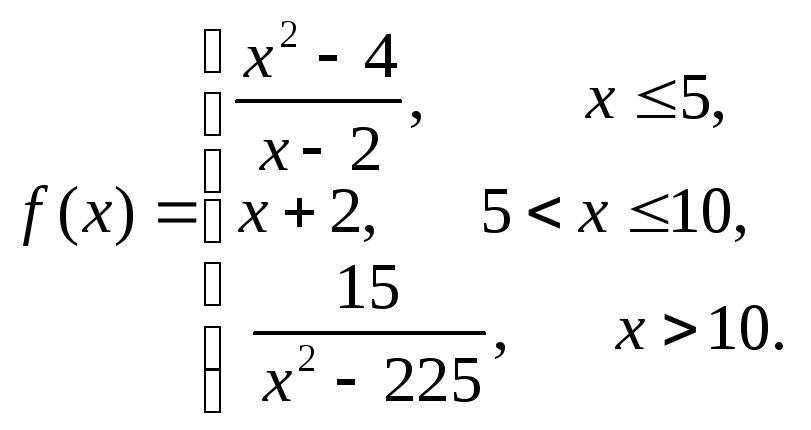
2) Шаг1.– отметим, что мы не стали исключать точку, поскольку она не удовлетворяет условию.Шаг2. Точкииявляются точно точки разрыва, поскольку в них функция не определена (осталось только их классифицировать); кроме того, необходимо исследовать поведение функции в– точке смены аналитической зависимости.Шаг3.:поэтому данная точка является точкой устранимого разрыва.Шаг4.:,поэтому данная точка является точкой разрываI– го рода (односторонние пределы конечны, но не равны между собой).Шаг5.:поэтому данная точка является точкой разрываII– го рода (как минимум один односторонний предел равен бесконечности).

Ответ.Функция является непрерывной на всей числовой оси за исключением точек(точка устранимого разрыва),(точка разрываI– го рода),(точка разрываII– го рода).

Определение 3.24.Функция называется непрерывной на интервале, если она непрерывна в каждой точке данного интервала. Функция называется непрерывной на отрезке, если она непрерывна на интервале, непрерывна справа в точкеи непрерывна слева в точке.

Теорема 3.10.Элементарные функции непрерывны на области определения.Без доказательства. Для неэлементарных функций подобное утверждение неверно. Например, функцияопределена на всей числовой примой и при этом разрывная при всех целых значениях.

Теорема 3.11.(свойства функции, непрерывной на отрезке). Пусть функциянепрерывна на отрезке, тогда она: 1) ограничена на этом отрезке; 2) достигает на этом отрезке своих наибольшего значенияи наименьшего значения; 3)- функция принимает все возможные значения из промежутка