
Лисенко В.І.
«Вища математика»
І КУРС
Опорні конспекти лекцій
Лекція №17-18. Границя та неперервність.
Література:
-
Гусак А.А. Высшая математика: учебник для студентов вузов. В 2 т. Т.1. – Минск: ТетраСистемс, 2007 – 544с. (76-91 с.).
-
Каплан И.А., Пустынников В.И. Практикум по высшей математике: в 2.Т., Т.1.: – М.: Эксмо, 2008. – 576 с. (с. 213-219, 293-315).
-
Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч.І. – К.: Кондор, 2006. –588с. (с. 278 - 329).
-
Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум: Навчальний посібник: К.: Центр навч. Літератури, 2005 – 536с. (с. 137-160).
Основні теоретичні положення
-
Функція.
Нехай
задані дві непорожні множини
![]() та
та
![]() .
.
Озн.1.
Якщо
кожному значенню змінної
![]() ,
ставиться у відповідність за деяким
законом єдине значення
,
ставиться у відповідність за деяким
законом єдине значення
![]() ,
то кажуть, що на множині
,
то кажуть, що на множині
![]() задана функція
задана функція
![]() (1).
(1).
Функція
задана формулою (1) називається явною,
а функція задана формулою
![]() (2) називається неявною (рівняння не
розв’язане відносно у).
(2) називається неявною (рівняння не
розв’язане відносно у).
Множина
Х називається областю визначення функції
і позначається
![]() .
Множина
.
Множина
![]() всіх значень у, які
всіх значень у, які
![]() приймає при
приймає при
![]() ,
називається областю (множиною) значень
функції і позначається
,
називається областю (множиною) значень
функції і позначається
![]() .
При цьому х називається незалежною
змінною або аргументом, а у – функцією.
.
При цьому х називається незалежною
змінною або аргументом, а у – функцією.
-
Деякі класи функцій.
Обмежені
функції.
Функція
![]() ,
визначена на множині Х,
називається обмеженою, якщо існує таке
число
,
визначена на множині Х,
називається обмеженою, якщо існує таке
число
![]() ,
що для всіх
,
що для всіх
![]() виконується нерівність
виконується нерівність
![]() .
Наприклад:
.
Наприклад:
![]() ,
,
![]() .
.
Монотонні
функції.
Функцію називають зростаючою на проміжку
![]() ,
якщо більшому значенню аргумента з
цього проміжку відповідає більше
значення функції. Записують:
,
якщо більшому значенню аргумента з
цього проміжку відповідає більше
значення функції. Записують:
![]() ,
,
![]() ,
тоді
,
тоді
![]() і навпаки. Наприклад
і навпаки. Наприклад
![]() зростає при
зростає при
![]() .
.
Якщо
ж при
![]()
![]() ,
то функцію називають неспадною.
,
то функцію називають неспадною.
Парні та непарні функц1ї.
Функція
![]() називається парною (непарною), якщо її
область визначення симетрична відносно
точки
називається парною (непарною), якщо її
область визначення симетрична відносно
точки
![]() і
і
![]() (
(![]() ).
Наприклад
).
Наприклад
![]() ,
,
![]() – парні, а
– парні, а
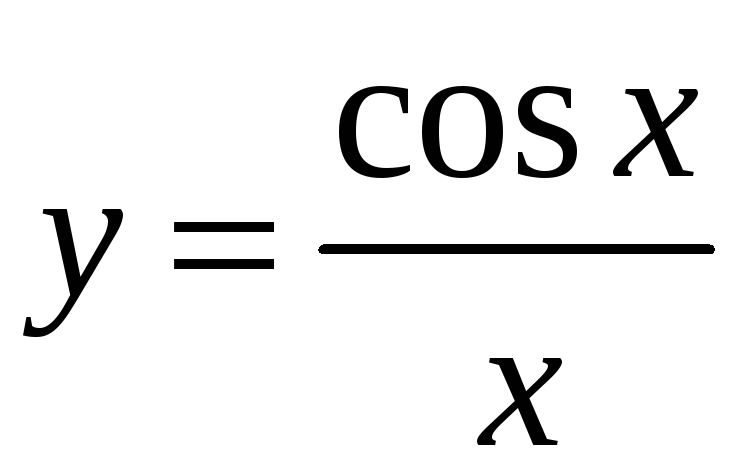 ,
,
![]() –
непарні.
–
непарні.
Періодичні функції
Функція
називається періодичною, якщо існує
таке число
![]() ,
що для всіх
,
що для всіх
![]() виконується умова
виконується умова
![]() .
Наприклад
.
Наприклад
![]() ;
;
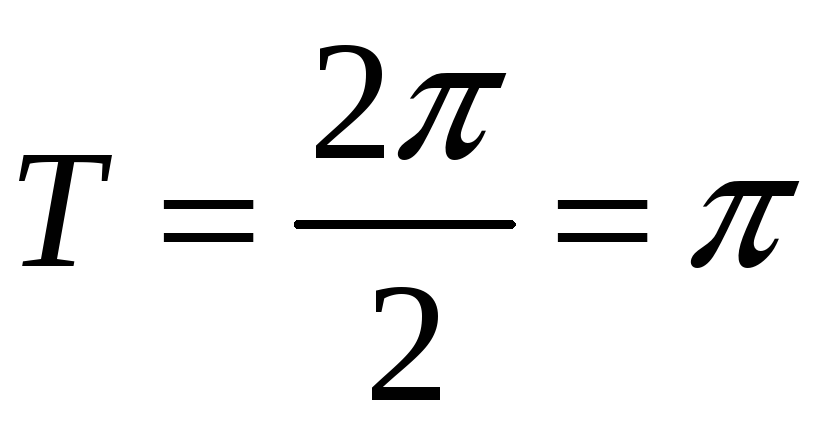 – найменший період.
– найменший період.
![]() –загальний період.
–загальний період.
-
Основні елементарні функції.
-
Степенева функція:
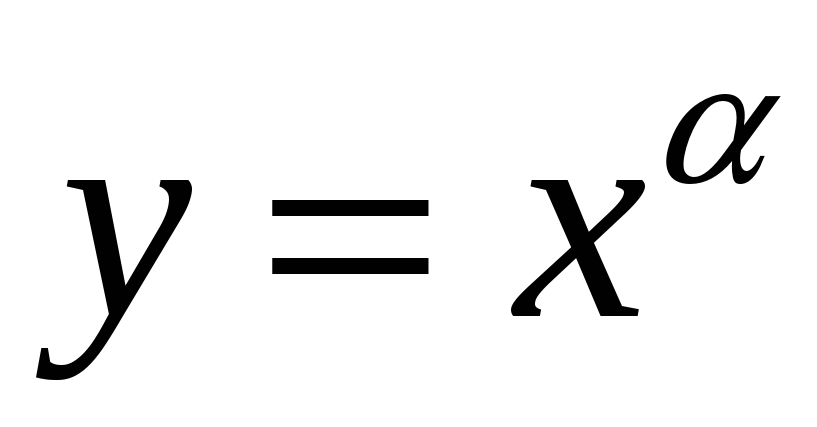 ,
,
 .
. -
Показникова функція:
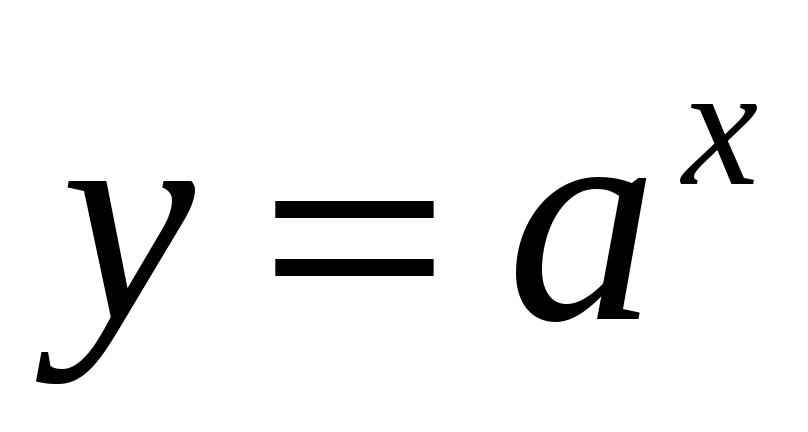 ,
,
 ,
,
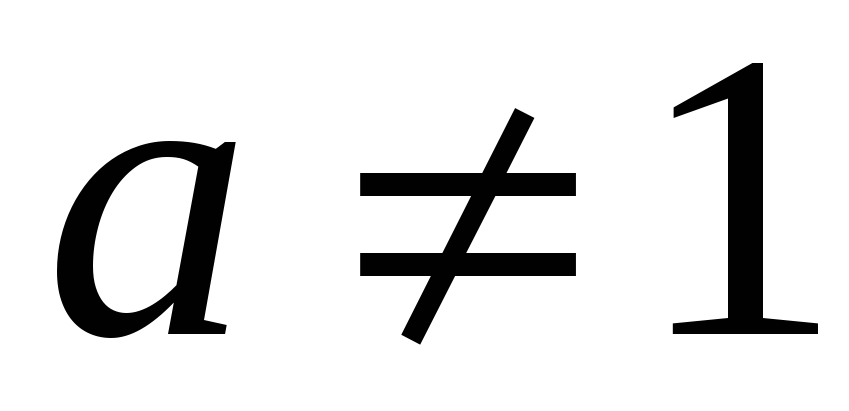 .
. -
Логарифмічна функція:
 ,
,
 ,
,
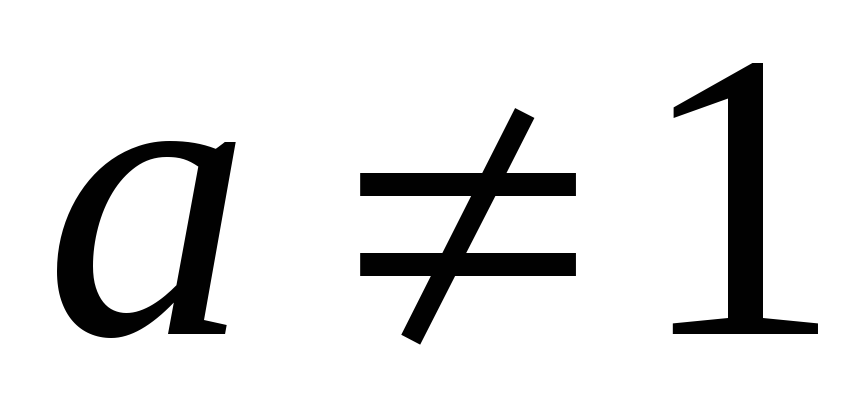 .
. -
Тригонометрична функція:
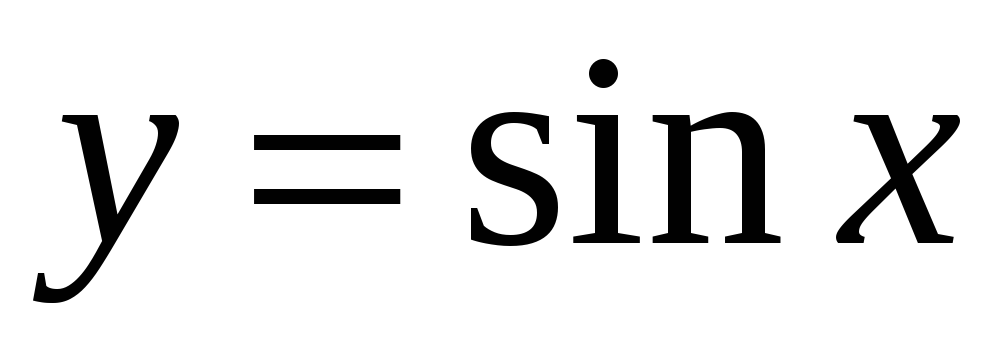 ,
,
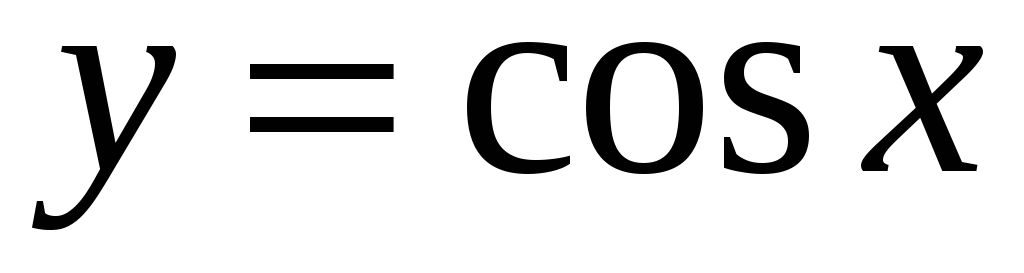 ,
,
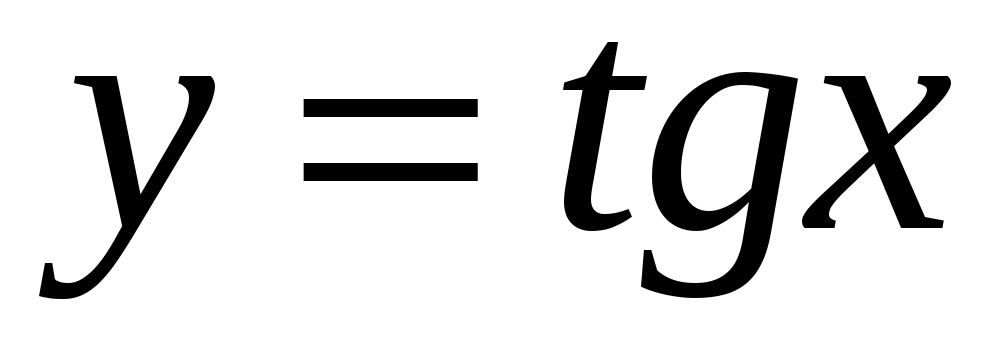 ,
,
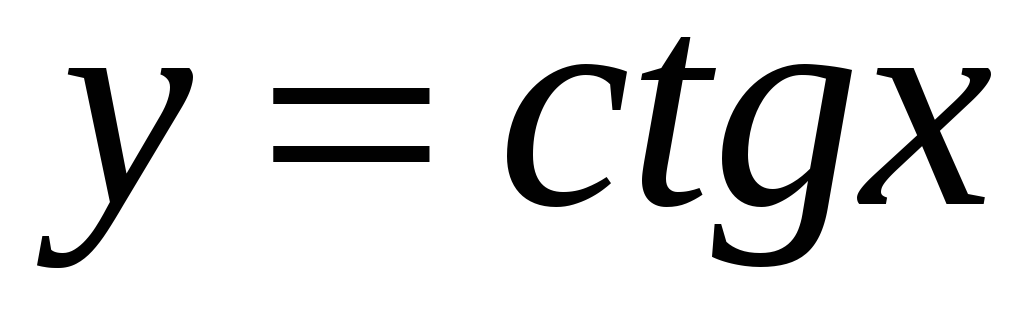 .
. -
Обернені тригонометричні функції: :
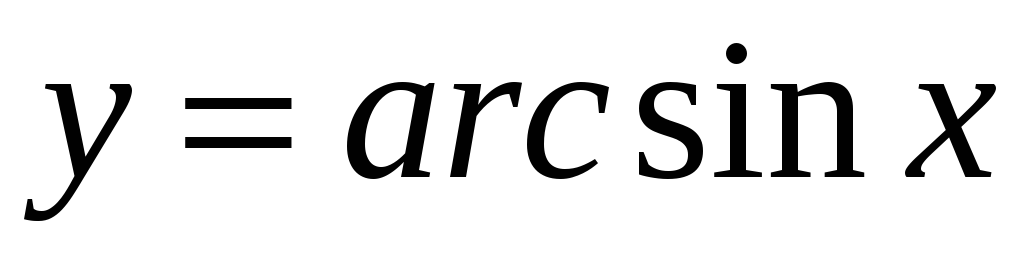 ,
,
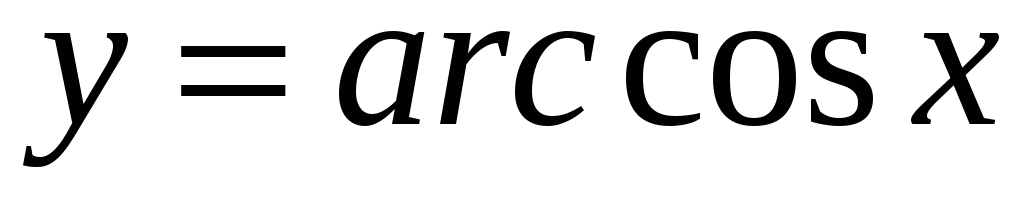 ,
,
 ,
,
 .
.
Елементарними називають функції, які одержують з основних елементарних функцій за допомогою скінченного числа арифметичних дій.
До елементарних функцій відносяться гіперболічні функції, які визначаються так:
Гіперболічний
синус:
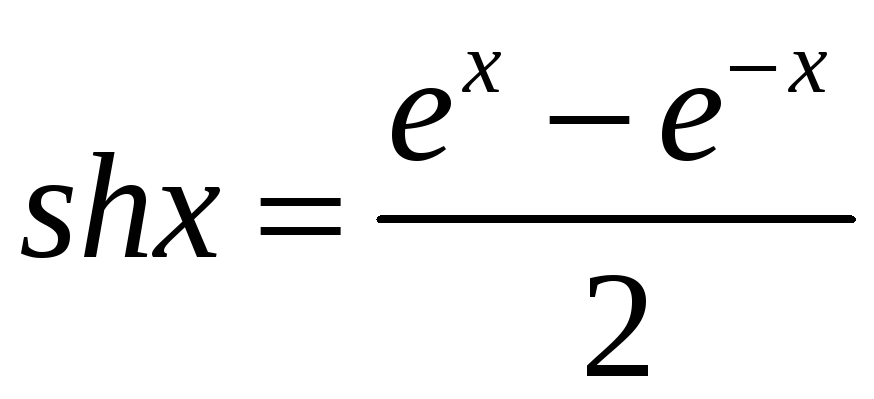 ;
;
Гіперболічний
косинус:
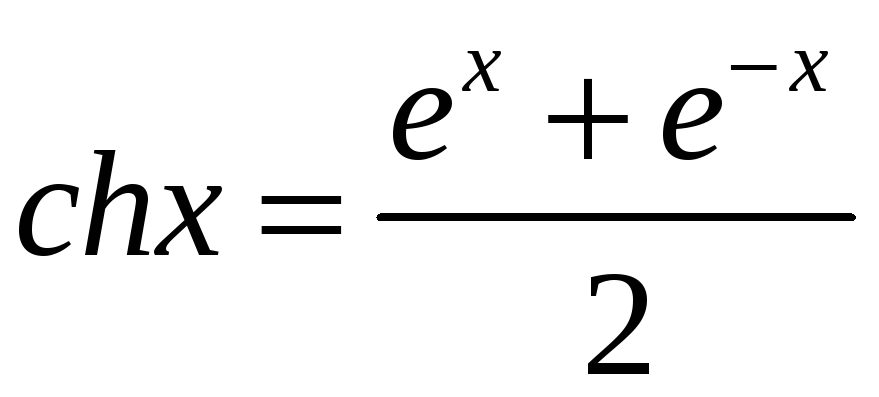 ;
;
Гіперболічний
тангенс:
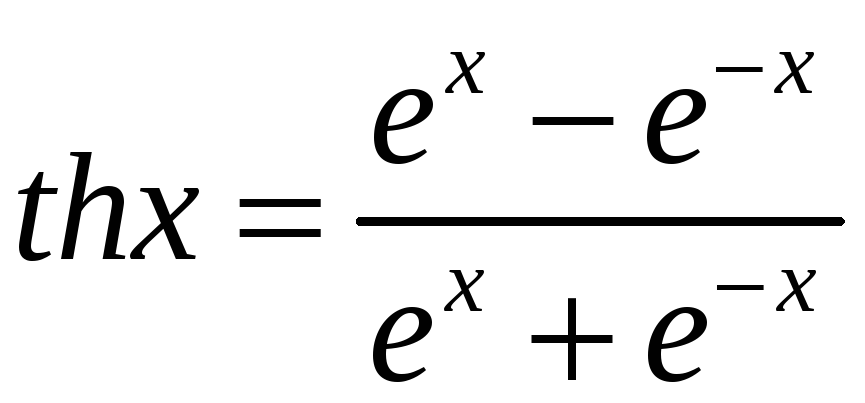 ;
;
Гіперболічний
котангенс:
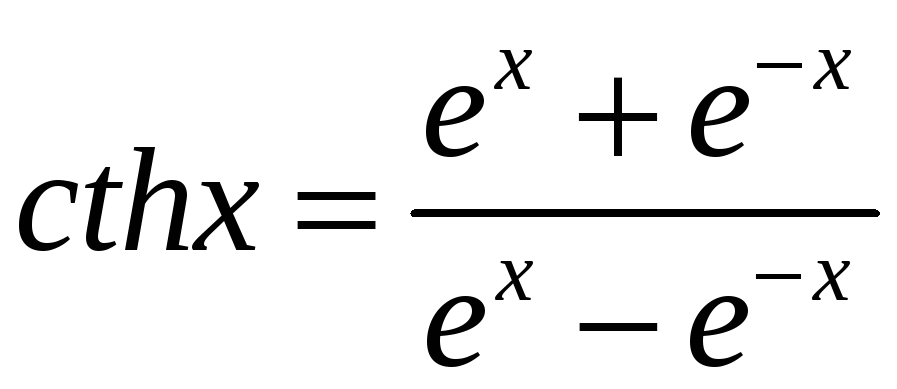 .
.
Увага! Самостійно повторити властивості і графіки основних елементарних функцій (1-5).
-
Границя функції.
Нехай
функція
![]() визначена в деякому околі точки
визначена в деякому околі точки
![]() ,
за виключенням, можливо самої точки
,
за виключенням, можливо самої точки
![]() .
.
Озн.2.
Число А називають границею функції
![]() в точці
в точці
![]() ,
якщо для довільного числа
,
якщо для довільного числа
![]() знайдеться число
знайдеться число
![]() ,
яке залежить від
,
яке залежить від
![]() ,
таке, що для всіх х, які задовольняють
нерівність
,
таке, що для всіх х, які задовольняють
нерівність
![]() виконується нерівність
виконується нерівність
![]() .
Символічно записують
.
Символічно записують
![]() (3)
(3)
Увага!
Користуючись рис.1, поясніть, чому за
![]() –окіл
точки
–окіл
точки
![]() ,
обрано менший з відрізків
,
обрано менший з відрізків
![]() і
і
![]() .
.

Рис 1.
Якщо
![]() ,
то функція називається нескінченно
великою при
,
то функція називається нескінченно
великою при
![]() .
.
Якщо
![]() ,
то функція називається нескінченно
малою при
,
то функція називається нескінченно
малою при
![]() .
.
Якщо
![]() і
і
![]() ,
то пишуть
,
то пишуть
![]() ,
якщо ж
,
якщо ж
![]() то пишуть
то пишуть
![]() .
.
Числа
![]() (4) та
(4) та
![]() (5) називають відповідно границею
функції
(5) називають відповідно границею
функції
![]() зліва в точці
зліва в точці
![]() і границею функції
і границею функції
![]() справа в точці
справа в точці
![]() .
.
Якщо
![]() ,
то замість
,
то замість
![]() пишуть
пишуть
![]() ,
а замість
,
а замість
![]() пишуть
пишуть
![]() .
.
Числа (4) і (5) називають односторонніми границями.
Для
існування границі функції при
![]() необхідно і достатньо, щоб
необхідно і достатньо, щоб
![]() (6).
(6).
Приклад 1.
Довести
що
![]()
Розв’язання.
Для розв’язання
задачі треба для довільного
![]() знайти
знайти
![]() -окіл
точки
-окіл
точки
![]() .
Тобто
.
Тобто
![]()
(3): ![]() (*)
(*)
Розв’яжемо
нерівність (*) відносно
![]() .
.
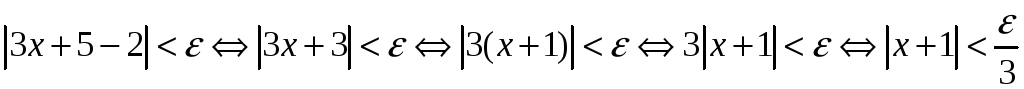 Значить
Значить
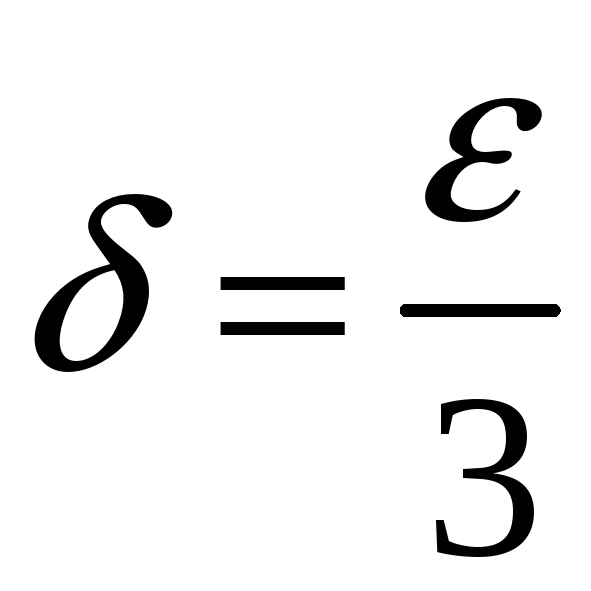 .
.
