
- •Интегральное исчисление Лекция № 25. Тема 1: Неопределённый интеграл
- •1.1. Первообразная и неопределённый интеграл
- •Лекция № 26
- •1.5. Интегрирование некоторых функций, содержащих квадратный трёхчлен
- •1.6. Интегрирование по частям
- •1.7. Многочлены и рациональные дроби
- •Лекция № 27
- •1.8. Интегрирование рациональных дробей
- •1.9. Интегрирование тригонометрических функций
- •Лекция № 28
- •1.10. Интегрирование некоторых иррациональных функций
- •1.11. Понятие о неберущихся интегралах
- •Лекция № 29. Тема 2 : Определённый интеграл
- •2.1. Задачи, приводящие к понятию определённого интеграла
- •2.2. Определение определённого интеграла
- •2.3. Основные свойства определённого интеграла
- •4. .
- •2.4. Интеграл как функция верхнего предела
- •Лекция № 30
- •2.7. Интегрирование по частям в определённом интеграле
- •Лекция № 31. Тема 3 : Приложения определённого интеграла
- •3.1. Площадь плоской фигуры
- •3.2. Длина дуги плоской кривой
- •3.3. Площадь поверхности тела вращения
- •3.4. Вычисление объёма тела по площадям поперечных сечений
- •Лекция № 32
- •3.5. Приложения определённого интеграла к некоторым задачам физики
- •Тема 4 : Несобственные интегралы
- •4.1. Несобственные интегралы первого рода (с бесконечными пределами)
- •4.2. Несобственные интегралы второго рода (от разрывных функций)
- •Функции нескольких переменных Лекция № 33. Тема 1 : Предел. Непрерывность. Частные производные
- •1.1. Определение функции нескольких переменных
- •1.2. Предел и непрерывность функции двух переменных
- •1.3. Частные производные функции двух переменных
- •1.4. Полный дифференциал функции двух переменных
- •1.5. Производная сложной функции
- •2.4. Производная по направлению
- •2.5. Градиент функции
- •Лекция № 35
- •2.6. Касательная и нормаль к поверхности
- •Тема 3* : Векторная функция скалярного аргумента
- •3.1. Векторная функция. Предел. Непрерывность
- •3.2. Производная векторной функции
- •. Лекция № 36. Тема 4 : Экстремум функции нескольких переменных
- •4.1. Необходимые условия экстремума
- •4.2. Достаточные условия экстремума
- •4.3. Нахождение наибольшего и наименьшего значений функции
- •Лекция № 37
- •4.4. Условный экстремум
- •4.5. Метод наименьших квадратов
- •Дифференциальные уравнения Лекция № 38. Тема 1 : Введение
- •1.1. Задачи, приводящие к дифференциальным уравнениям
- •1.2. Определение дифференциального уравнения
- •Тема 2: Дифференциальные уравнения первого порядка
- •2.1. Общие понятия. Теорема существования и единственности
- •2.2. Уравнения с разделяющимися переменными
- •Лекция № 39
- •2.3. Однородные уравнения
- •Лекция № 40. Тема 3 : ду высших порядков
- •3.1. Определение ду п-го порядка
- •3.2. Уравнения, допускающие понижение порядка
- •4.2. Теорема о структуре общего решения лоду-2
- •Лекция № 41
- •4.3. Лоду-2 с постоянными коэффициентами
- •4.4. Линейные неоднородные дифференциальные уравнения второго порядка
- •4.5. Метод вариации произвольных постоянных (метод Лагранжа)
- •Лекция № 42
- •4.6. Лнду-2 с постоянными коэффициентами со специальной правой частью
- •6.2. Решение нормальных систем ду методом исключений
Лекция № 39
2.3. Однородные уравнения
Определение 1.
Функция
![]() называетсяоднородной
функцией,
если
называетсяоднородной
функцией,
если
![]() выполняется
выполняется![]() .
.
Например, функция
![]() является однородной, так как
является однородной, так как
 .
.
Определение 2.
Уравнение вида
![]() называется однородным уравнением, если
называется однородным уравнением, если![]() однородная функция.
однородная функция.
Покажем, что решение однородного уравнения сводится к решению уравнения с разделяющимися переменными.
По условию
![]() .
Положим в этом тождестве
.
Положим в этом тождестве![]() ,
тогда
,
тогда

и уравнение примет вид
![]() .
.
Сделаем замену
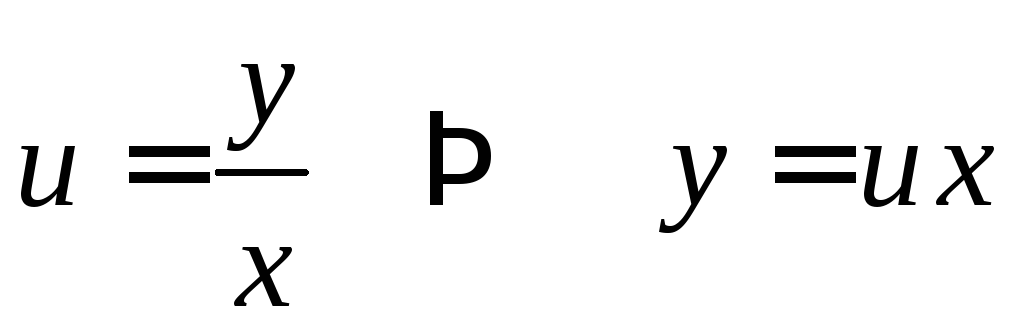 и
и![]() .
.
Тогда получим уравнение с разделяющимися переменными

Интегрируя его,
а затем, подставляя
 ,
находим решение.
,
находим решение.
Замечание.
Аналогично, как и для уравнений с
разделяющимися переменными, если
![]() ,
то однородное уравнение обладает
решением
,
то однородное уравнение обладает
решением![]() или
или![]() .
.
П ример
1. Определить
кривую, проходящую через точку
ример
1. Определить
кривую, проходящую через точку
![]() ,
еслиподкасательная
АВ
любой её точки есть среднее арифметическое
координат.
,
еслиподкасательная
АВ
любой её точки есть среднее арифметическое
координат.
Если
![]()
текущая точка у
текущая точка у
кривой, то по условию задачи,
получаем уравнение
![]()
![]() у
у
Получили однородное
урав-
![]()
нение, поэтому сделаем замену О А В х
![]() и
и
![]() .
.
Тогда уравнение примет вид
![]() .
.
Разделяем переменные

и интегрируем
 .
.
Выполнив обратную
замену
 ,
имеем
,
имеем
 .
.
Окончательно, учитывая, что кривая проходит через заданную точку и подставляя в общее решение ее координаты

находим
![]() и получим искомое уравнение кривой
и получим искомое уравнение кривой
![]() .
.
2.4. Линейные уравнения первого порядка (ЛУ–1)
Определение 3.
Уравнение вида
![]() ,
где
,
где![]() и
и![]() функции непрерывные на отрезке
функции непрерывные на отрезке![]() ,
называется линейным.
,
называется линейным.
Его решение будем искать в виде
![]() .
(1)
.
(1)
Продифференцируем выражение (1), а, затем подставим в ЛУ-1, получим
![]() .
(2)
.
(2)
Функцию
![]() выберем из условия
выберем из условия
![]() .
.
Проинтегрируем это уравнение
![]() .
.
Тогда уравнение (2) примет вид
![]() .
.
Окончательно, имеем
 .
.
Пример 2.
Найти общее решение уравнения
 .
.
Решение ищем в
виде
![]() .
Тогда для функции
.
Тогда для функции![]() получаем уравнение
получаем уравнение
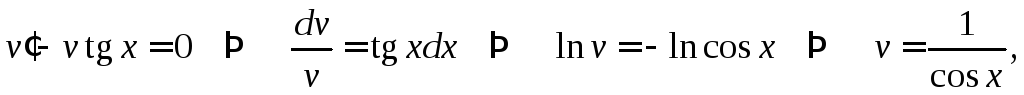
а для функции
![]()

Окончательно, имеем
 .
.
2.5. Уравнения Бернулли
Определение 4.
Уравнение вида
![]() ,
где
,
где![]() ,
называется уравнением Бернулли.
,
называется уравнением Бернулли.
Отметим, что при
![]() оно становится линейным, а при
оно становится линейным, а при![]()
уравнением с разделяющимися переменными.
Поэтому в дальнейшем эти случаи не
рассматриваем.
уравнением с разделяющимися переменными.
Поэтому в дальнейшем эти случаи не
рассматриваем.
Покажем, что
уравнение Бернулли путём замены
![]() ,
приводится к линейному. Действительно,
,
приводится к линейному. Действительно,
 .
.
Таким образом, уравнения Бернулли интегрируются аналогично как линейные.
Пример 3.
Найти общее решение уравнения
![]() .
.
Разделим данное
уравнение на
![]() и получим уравнение Бернулли
и получим уравнение Бернулли
![]() .
.
Здесь
![]() .
Решение ищем в виде
.
Решение ищем в виде![]() .
Тогда
.
Тогда
![]() .
.
Для функции
![]() получаем уравнение
получаем уравнение
![]() ,
,
а для функции
![]()

Проинтегрируем
это уравнение, тогда
![]() .
.
Таким образом, общее решение имеет вид
 .
.
2.6. Уравнения в полных дифференциалах
Определение 5.
Уравнение вида
![]() ,
называется уравнением в полных
дифференциалах, если
,
называется уравнением в полных
дифференциалах, если
![]() ,
(3)
,
(3)
где частные производные непрерывны в некоторой области.
Покажем, что равенство (3) является условием полного дифферен-циала.
Теорема.
Если
![]() полный дифференциал некоторой функции
полный дифференциал некоторой функции![]() ,
то выполняется условие (3). Верно и
обратное.
,
то выполняется условие (3). Верно и
обратное.
Пусть выражение
![]() является полным дифференциалом. Это
означает, что
является полным дифференциалом. Это
означает, что![]() ,
так как
,
так как
![]() .
.
Продифференцировав первое полученное выражение по у, а второе по х, получим
![]() .
.
Обратно. Пусть
выполняется условие (3). Требуется найти
функцию
![]() ,
которая должна удовлетворять условиям:
,
которая должна удовлетворять условиям:
 .
.
Интегрируя первое из них, получим

где
![]() является фиксированной точкой из области
определения функций
является фиксированной точкой из области
определения функций![]() и
и![]() ,
а
,
а![]()
произвольная функция. Теперь
продифференцируем это выражение:
произвольная функция. Теперь
продифференцируем это выражение:

и воспользуемся условием (3)

откуда
![]() и
и
 .
.
Таким образом,
функция
![]() найдена
найдена
 .
(4)
.
(4)
Теорема доказана. Возвращаемся к уравнению в полных дифферен-циалах. Если выполняется условие (3), то согласно теореме имеем
![]() общий интеграл.
общий интеграл.
С учётом формулы (4) окончательно определяем общий интеграл уравнения в полных дифференциалах
 .
(5)
.
(5)
Пример 4. Решить задачу Коши

Проверим выполнение условия (3):
![]() ,
,
т.е. имеем уравнение в полных дифференциалах. По формуле (5) получаем

или
![]() .
.
Приведём подобные члены и соберём все константы в одну:
![]() .
.
Значение константы
С
определим из начального условия:
![]() .
.
Тогда решение задачи Коши будет иметь вид
![]() .
.
