1.11. Понятие о неберущихся интегралах

Теорема существования неопределённого интеграла утверждает, что всякая , непрерывная на, имеет на этом интервале первообразную. Однако из этого не следует, что интеграл от любой элементарной функции выражается через элементарные функции. Такие интегралы называютсянеберущимися в элементарных функциях. Они порождают новые, неэлементарные функции.

К таким интегралам, например, относятся:

интеграл Пуассона;

интегральные синус и косинус;

интегралы Френеля;

интегральный логарифм и многие другие.

Существуют другие методы для их нахождения с использованием так называемых специальных функций, функциональных рядов и т.п.

Лекция № 29. Тема 2 : Определённый интеграл

2.1. Задачи, приводящие к понятию определённого интеграла

1. Задача о площади криволинейной трапеции.

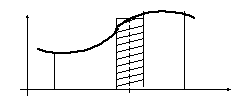Пусть на задана функция. Требуется найти пло-щадьS фигуры, образованной осью Ox, прямыми: играфиком функции (криволинейная трапеция).

у

x

О а х_i-1 x_i b

Разобьём нап частей: . На каждом участке разбиениявыберем точкуи составим сумму

, где . (1)

Тогда , так какS_п геометрически представляет собой площадь ступенчатой фигуры. Если теперь перейти к пределу в формуле (1), когда , то получим значение площади криволинейной трапеции, т.е.

.

2. Задача о массе тела.

Задан линейный неоднородный стержень с плотностью , лежащий в пределах. Требуется определить его массуМ. Аналогично разобьём его на части. Так как в пределах плотностьизменяется мало, то, а масса стержня

.

Точное значение массы получим, если перейти к пределу, когда .

.

2.2. Определение определённого интеграла

Пусть на задана функция. Разделимна части произвольным образом точками:. На каждом из полученных отрезков разбиенияпроизвольно выберем точкуи составим сумму

, где , (2)

называемую интегральной суммой функции на отрезке.

Определение 1. Если предел интегральной суммы (2) не зависит от способа разбиения отрезка и выбора точек, то он называется опре-делённым интегралом от функциина отрезкеи обозначается

, (3)

где а - нижний, b - верхний пределы интегрирования.

Определение 2. Если для насуществует предел (3), то функцияназываетсяинтегрируемой на .

При каких условиях существует предел (3)?

Теорема 1 (теорема существования определённого интеграла). Если непрерывна на , то она интегрируема на .

Замечание. Среди разрывных функций на есть как интегри-руемые (ограниченные монотонные), так и неинтегрируемые. Например, неинтегрируемой является функция Дирихле

D (x) =

Действительно, если в качестве точек выбрать рациональные точки и рассмотреть функцию Дирихле на отрезке, то из формулы (3) следует

а если выбрать иррациональные точки, то

Таким образом, предел (3) не существует.

Теперь выясним геометрический смысл определённого интеграла:

Из ранее рассмотренной задачи при  это площадь криволинейной трапеции. При  это тоже площадь, но со знаком минус. Поэтому определённый интеграл – это алгебраическая площадь криволинейной трапеции.

у

х



Физический смысл определённого интеграла.

Из ранее рассмотренной задачи масса стержня с линейной плотностью определяется как.

Аналогично рассуждая, получаем: если - сила, действующая вдоль прямолинейного участка, то работа этой силы.