3. Заряд равномерно распределен по бесконечной плоскости.

Рассмотрим поле, созданное бесконечно протяженной плоскостью, заряженной равномерно с поверхностной плотностью заряда s. Эта величина характеризует распределение заряда по поверхности и численно равна заряду, приходящемуся на единицу площади:

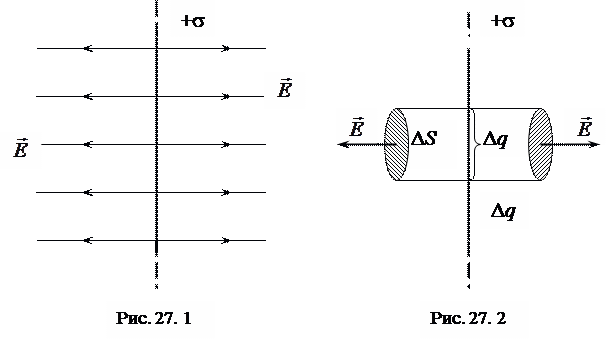
где Dq – заряд на площади DS. Если заряд равномерно распределен по всей поверхности, то поверхностная плотность его во всех точках одинакова. Единица поверхностной плотности заряда - кулон на метр в квадрате (Кл/м2). Полагая, что заряд плоскости положительный, определим направление линий напряженности. Из соображений симметрии следует, что точечный пробный заряд будет отталкиваться от бесконечной заряженной плоскости, в каком бы месте он ни располагался. Это означает, что линии напряженности направлены перпендикулярно плоскости (рис. 27.1).

Если выбрать две точки, расположенные симметрично относительно плоскости, то напряженность поля в этих точках по модулю будет одинакова

3. Две параллельные равномерно заряженные бесконечные пластины.

Найдем распределение потенциала поля, создаваемого двумя одинаковыми равномерно заряженными параллельными пластинами, заряды которых равны по модулю и противоположны по знаку1 (рис. 279).

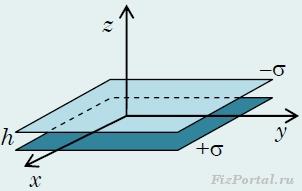
Обозначим поверхностную плотность заряда на одной пластине +σ, а на другой −σ. Расстояние между пластинами h будем считать значительно меньшим размеров пластин. Введем систему координат, ось z которой перпендикулярна пластинам, начало координат разместим по средине между пластинами. Очевидно, для бесконечно больших пластин все характеристики поля (напряженность и потенциал) зависят только от координаты z. Для расчета напряженности поля в различных точках пространства воспользуемся полученным выражением для напряженности поля, создаваемого бесконечной равномерно заряженной пластиной и принципом суперпозиции.

Каждая равномерно заряженная пластина создает однородное поле, модуль напряженности которого равен Eo = σ/(2εo), а направления указаны на рисунке 280, 281

.

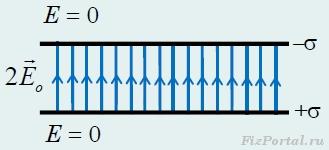
Складывая напряженности полей по принципу суперпозиции, получим, что в пространстве между пластинами напряженность поля E = 2Eo = σ/εo вдвое превышает напряженность поля одной пластины (здесь поля отдельных пластин параллельны), а вне пластин поле отсутствует (здесь поля отдельных пластин противоположны).

 Строго говоря, для пластин конечных размеров поле не является однородным

3. Дифференциальная форма теоремы гаусса:

Дифференциальная (или локальная) форма теоремы Гаусса расширяет ее возможности как инструмента исследования и расчета. В дифференциальной форме теоремы устанавливается связь между объемной плотностью заряда и изменениями напряженности поля в окрестности данной точки пространства.

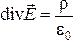Это уравнение и выражает теорему Гаусса в дифференциальной форме. В дифференциальной форме теорема Гаусса является локальной теоремой: дивергенция напряженности поля в данной точке зависит только от плотности электрического заряда ρ в той же точке и больше ни от чего. Это одно из замечательных свойств электрического поля. Например, в разных точках поля точечного заряда поле E отличается друг от друга. Это же относится, вообще говоря, и к пространственным производным ¶Ex /¶x, ¶Ey /¶y, ¶Ez /¶z. Однако, как утверждает теорема Гаусса, сумма этих производных, которая определяет дивергенцию E, оказывается во всех точках поля (вне самого заряда) равной нулю.

В тех точках поля, где дивергенция E положительна, мы имеем источники поля (положительные заряды), а в тех точках, где она отрицательна, − стоки (отрицательные заряды). Линии вектора E выходят из источников поля, а в местах стоков они заканчиваются

3. Потенциальная энергия точечного заряда в электростатическом поле точечного заряда

для точечного заряда, находящегося в электростатическом поле можно ввести потенциальную энергию взаимодействия U(x,y,z). Эта функция имеет следующий физический смысл: работа электрического поля при перемещения точечного заряда из одной точки с координатами (x1,y1,z1) в другую, с координатами (x2,y2,z2) равна изменению потенциальной энергии, взятому с противоположным знаком:

A= - ∆U= - (U(x2, y2, z2) – U(x1, y1, z1))

Изменение знака в данном определении достаточно логично: если электрическое поле совершило положительную работу (A > 0), то его энергия уменьшается (ΔU < 0).

3. Потенциал поля точечного заряда. Потенциал электростатического поля системы точечных зарядов.

Потенциал электростатического поля — скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду

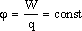
- энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.

- следствие принципа суперпозиции полей (потенциалы складываются алгебраически).

Потенциал поля точечного заряда

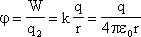
Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Qi (i = 1, 2, ... , n). Энергия взаимодействия всех n зарядов определится соотношением

где rij - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз.