2.3. Диференціальне рівняння екстремалей функціоналу, в який входять похідні вищих порядків (рівняння Ейлера-Пуассона)

Ставиться задача знаходження мінімуму (максимуму) функціоналу

при крайових умовах

Із необхідної умови екстремуму приівипливає, що допустимі екстремалі є розв'язками диференціального рівнянняпри крайових умовах

Розв'язки останнього диференціального рівняння називаються екстремалями, а саме рівняння називається диференціальним рівнянням екстремалей або рівнянням Ейлера-Пуассона.

Приклад 8.Знайти екстремалі функціоналу, які задовольняють вказаним крайовим умовам (допустимі екстремалі):

а) 

б)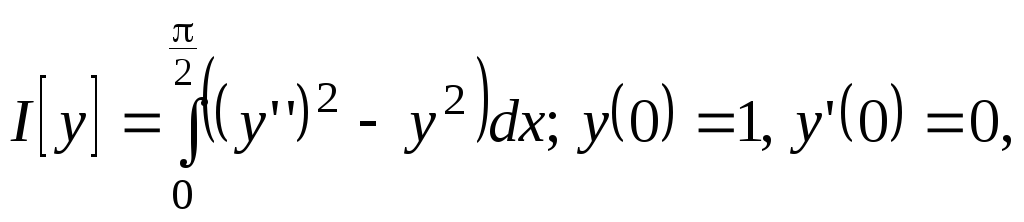 

в) 

Розв'язання. а) Знайдемо похідні, що входять в рівняння Ейлера-Пуассона:

Тоді рівняння Ейлера-Пуассона набуває вигляду:

Розв'яжемо одержане рівняння:

—екстремалі, де — довільні сталі.

Допустимі екстремалі знайдемо, визначивши конкретні значення із крайових умов:

Отже, допустима екстремаль

б) Знайдемо похідні, що входять в рівняння Ейлера-Пуассона:

Тоді рівняння Ейлера-Пуассона

набуває вигляду

Розв'яжемо останнє рівняння:

— екстремалі.

Конкретні значення знайдемо з крайових умов:

Отже, допустима екстремаль

в) Знайдемо похідні, що входять в рівняння Ейлера-Пуассона:

Тоді рівняння Ейлера-Пуассона

набуває вигляду

Розв'яжемо останнє рівняння:

—екстремалі, де — довільні сталі.

Використавши крайові умови, знайдемо значення .

Спочатку із крайових умов визначаємо.

Тоді на основі крайових умов одержуємо систему для знаходження:

Отже, допустима екстремаль

2.4. Система диференціальних рівнянь

Екстремалей функціоналу, що залежить

Від кількох функцій (система рівнянь

Ейлера-Лагранжа)

Ставиться задача знаходження мінімуму (максимуму) функціоналу

при крайових умовах

Із необхідної умови екстремуму приівипливає, що допустимі екстремалі є розв'язками системи диференціальних рівнянь

при крайових умовах

Розв'язки останньої диференціальної системи називаються екстремалями, а сама система — системою диференціальних рівнянь екстремалей або системою рівнянь Ейлера-Лагранжа.

Приклад 9. Знайти екстремалі функціоналу, які задовольняють вказаним крайовим умовам (допустимі екстремалі):

а) 

б) 

Розв'язання.а) Знайдемо похідні, що входять в систему рівнянь Ейлера-Лагранжа:

Тоді система рівнянь Ейлера-Лагранжа

набуває вигляду:

Розв'яжемо останню систему:

Конкретні значення довільних сталих знайдемо з крайових умов:

Отже, допустимі екстремалі:

б) Знайдемо похідні, що входять в систему рівнянь Ейлера-Лагранжа:

Тоді система рівнянь Ейлера-Лагранжа

набуває вигляду:

Розв'яжемо останню систему зведенням до одного диференціального рівняння вищого порядку:

Використавши крайові умови, знайдемо :

Отже, допустимі екстремалі:

2.5. Канонічні рівняння екстремалей

Розглянемо систему рівнянь Ейлера-Лагранжа

Позначимо Функціїназиваютьсяканонічними змінними для функціоналу

При цьому змінні іназиваютьсяспряженими. Введемо так звану функцію Гамільтона (гамільтоніан)

Знайдемо частині похідні гамільтоніана H по та:

Оскільки а з системи рівнянь Ейлера-Лагранжато мають місце співвідношення:

Одержана система називається канонічною системою рівнянь екстремалей для функціоналу

Задачі для самостійної роботи

1. Знайти екстремалі функціоналу, які задовольняють заданим крайовим умовам (допустимі екстремалі):

1.1. 

1.2. 

1.3. 

1.4. 

1.5. 

1.6. 

1.7. 

1.8. 

1.9. 

1.10. 

1.11. 

1.12. 

1.13. 

1.14. 

1.15. 

1.16. 

1.17. 

1.18. 

1.19. 

1.20. 

1.21. 

2. Знайти екстремалі функціоналу, які задовольняють вказаним крайовим умовам (допустимі екстремалі):

2.1. 

2.2. 

2.3. 

3. Знайти екстремалі функціоналу, які задовольняють вказаним крайовим умовам (допустимі екстремалі):

3.1. 

3.2. 

3.3. 

3.4. 

3.5. 

3.6.