3.3. Задача на екстремум функціоналу з рухомими кінцями. Умови трансверсальності

Ставиться задача знаходження мінімуму (максимуму) функціоналу серед неперервно диференційовних на відрізкуфункцій, якщо крайові умови не задані, але відомо, що точкиілежать відповідно на заданих лініяхі, причому числаітакож підлягають визначенню.

Сформульована задача називається варіаційною задачею з рухомими кінцями.

У даному випадку клас допустимих функцій, на яких шукається екстремум функціоналу, розширюється порівняно з ситуацією закріплених кінців, бо крім кривих порівняння, що мають спільні межові точки з досліджуваною кривою, можна брати криві зі зміщеними кінцевими точками. Це означає, що коли на якій-небудь функції функціоналдосягає екстремуму в задачі з рухомими кінцями, то екстремум тим паче досягається по відношенню до більш вузького класу кривих, які мають спільні межові точки з кривою, а, отже, функціяповинна бути розв'язком рівняння Ейлера

.

Загальний розв'язок рівняння Ейлера включає дві довільні сталі. Конкретні значення довільних сталих знаходяться при закріплених кінцях із крайових умов, а при рухомих — із додаткових умов, які називаютьсяумовами трансверсальності і мають вигляд:

Часто числа ізадані, і точкиіможуть переміщатися тільки вздовж вертикальних прямих відповідноі. Тоді умови трансверсальності набувають вигляду:

і називаються природними крайовими умовами.

Розглянемо виведення природних крайових умов. Варіація функціоналу визначається рівністю (п.2.2):

До другого доданка застосуємо метод інтегрування частинами (як в п.2.2) і одержимо:

.

На екстремалі перший доданок останньої рівності дорівнює нулю, і з необхідної умови екстремумувипливає:

Оскільки — довільна варіація і на кінцях може набувати будь-яких значень, то рівність варіації функціоналу нулю можлива у випадку

Якщо , то умова трансверсальності, наприклад, для лівого кінця має вигляд:або.

Якщо , тоабо. Останнє співвідношення є умовою перпендикулярності шуканої кривої, що доставляє екстремум функціоналу, і заданої лінії. Таким чином, поняття трансверсальності є деяким узагальненням поняття ортогональності.

Правилознаходження допустимих екстремалей варіаційної задачі з рухомими кінцями:

1. Скласти рівняння Ейлера , розв'язати його і знайти екстремалі .

2. Скласти систему алгебраїчних рівнянь для знаходження конкретних значень довільних сталих і тих чисел з париі, які невідомі. Для цього використати крайові умови, якщо на відповідному кінці вони задані, або природні крайові умови чи, в загальному випадку, умови трансверсальності разом з тими рівняннями перетину шуканої допустимої екстремаліз даними лініями,, які відповідають невідомим числам з париі:

.

3. Розв'язати одержану систему і знайти допустиму екстремаль.

Приклад 16. Знайти криву, на якій реалізується мінімум функціоналу при умові, що її лівий кінець розміщений в точці, а правий кінець — на прямій. Обчислити мінімальне значення функціоналу.

Розв'язання. Знайдемо похідні, що входять в рівняння Ейлера:

.

Тоді рівняння Ейлера набуває вигляду:.

Розв'яжемо це рівняння:

— екстремалі.

Допустима екстремаль повинна проходити через точку , тобто на лівому кінці задана крайова умова.

Звідси .

Правий кінець допустимої екстремалі ковзає по вертикальній прямій . Отже, там повинна виконуватись природна крайова умова

Підставивши в останній вираз похідну , одержимо:

Отже, допустима екстремаль .

Оскільки при, то згідно з посиленими достатніми умовами Лежандра на даній єдиній допустимій екстремалі реалізується мінімум функціоналу. Знайдемо його значення:

Приклад 17. Знайти найкоротшу відстань від точки до верхньої половини еліпса.

Розв'язання.Мова йде про мінімізацію функціоналу (довжини дуги)

при умові, що лівий кінець закріплений в точці , тобто, а правий — переміщується по верхній половині еліпса, тобто,.

Знайдемо похідні, що входять в рівняння Ейлера:

Тоді рівняння Ейлера набуває вигляду:

Звідси — екстремалі.

На правому кінці повинна виконуватись умова трансверсальності

Приєднавши до останнього співвідношення рівняння перетину екстремалі з еліпсом і крайову умову на лівому кінці, одержимо систему:

Розв'язавши її, знаходимо

.

Отже, допустима екстремаль . Оскільки згідно з геометричним змістом задачі функціонал має мінімум і допустима екстремаль єдина, то вона й реалізує мінімум. Знайдемо його значення:

Отже, найкоротша відстань дорівнює .

Приклад 18. Знайти найкоротшу відстань між параболою і прямою.

Розв'язання. Задача полягає в мінімізації функціоналу (довжини дуги) при умові, що лівий кінець допустимої екстремалі може рухатись вздовж параболи , а правий — вздовж прямої.

Для цього функціоналу рівняння Ейлера має загальний розв'язок (приклад 17).

Оскільки

то умови трансвер­сальності

набувають вигляду:

Звідси .

Використавши рівняння перетину екстремалі з даними лініями і, знайдемоі:

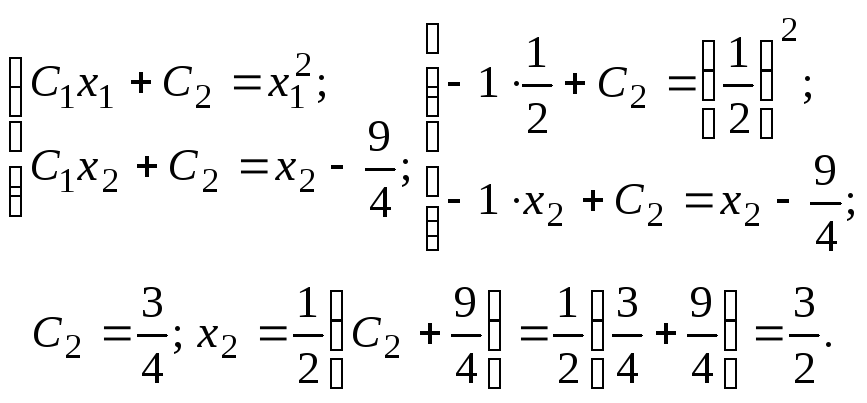
Отже, допустима екстремаль .

Знайдемо відповідне значення функціоналу:

Оскільки згідно з геометричним змістом задачі функціонал має мінімум і допустима екстремаль єдина, то на ній і досягається мінімум. Отже, найкоротша відстань дорівнює .

Приклад 19. Знайти криву , яка доставляє максимум функціоналупри умові, що її лівий і правий кінці належать відповідно лініямі.

Розв'язання. Складемо рівняння Ейлера :

Знайдемо загальний розв'язок: — екстремалі.

Конкретні значення довільних сталих ізнайдемо з умов трансверсальності

Отже, допустима екстремаль (шукана крива):