Биофизика / Методичка по математике

Частная производная по аргументу y . При этом аргумент x считаем постоянной величиной.

Z ′y =	∂Z	=	∂	(e	x+2 y	) = e	x+2 y ∂		(x + 2 y) = 2e	x+2 y
	∂y		∂y					∂y

Найти самостоятельно частные производные функций:

1)	Z = x2 + y 2	3)	Z = sin(xy)
2)	Z = e xy	4)	V = πr 2 h

Задачи для решения на практическом занятии

Найти частные производные функций:

1. Z = (x2 + y2 )2					5. Z = ex / y + e y / x
2.	Z =	x − y			6.	Z = cos y / x
		x + y				Z = ln(xy)
3.	Z = ln(x2 + y2 )				7.
4.	Z = x2 sin y
	8) Зависимость объема			V	газа, масса которого постоянна,
от температуры T и давления				P	выражается формулой V =		RT	, где
							P
R - постоянная.

Доказать, что P ∂∂VP +T ∂∂VT = 0 .

9.Z = 1 − x2 + y3

10.Z = x ln y

11.Z = cos x esin y

Т е м а 3

Дифференциалы функций одной и нескольких переменных

Понятие дифференциала функции тесно связано с понятием ее производной. Дифференциалом функции называется произведение производной этой функции на приращение ее аргумента, т.е.

dy = f ′(x) x . Таким образом, дифференциал функции пропорционален приращению аргумента. При достаточно малых приращениях аргумента величина приращения функции приближенно равна дифференциалу этой функции. На этом основано применение дифференциала функции в приближенных вычислениях.

Литература для подготовки к занятию по теме:

11

Ю.В.Морозов "Основы высшей математики и статистики", М., 1998, с.32-36, 56-58.

В процессе подготовки к практическому занятию по теме необходимо выполнить следующее:

1.Повторить следующие теоретические вопросы:

1)Дифференцирование сложной функции.

2)Правила дифференцирования функций вида y = u(x) ± v(x); y = kf (x)

3)Частные производные.

П. Изучить по указанной литературе следующие теоретические вопросы:

1)Понятие дифференциала функции.

2)Частный и полный дифференциалы.

3)Применение полного дифференциала в приближенных вы-

числениях.

Эталоны решения типовых задач и задачи для самоконтроля

Задача 1. Найти дифференциал функции y = 3x2 + ln(x +3) Решение

По определению дифференциала функции dy = y′(x)dx . Таким образом, задача нахождения дифференциала функции требует прежде всего нахождения производной функции. Используя правила

дифференцирования,							[1 (x +3)]′			получим:
′	2 ′	′		2	′			1
y (x) = (3x	)	+[ln(x +3)]	= 3(x		)	+	x +3	= 6x +
									x +3

В результате искомый дифференциал принимает вид:

		1
	dy = 6x +		dx
		x +3

Найти самостоятельно дифференциалы следующих функций:

1) y = sin 3x ,

2) y = (x2 +1)4 , 3) y = e2 x

Задача 2. Пользуясь понятием дифференциала, найти приближенно изменение силы тока в цепи с сопротивлением

R = 5000 Ом при напряжении на концах участка U =10 В, при увеличении сопротивления на R = 5 Ом.

Решение

По закону Ома I = UR . Учитывая, что изменение сопротивления

цепи мало по сравнению с величиной сопротивления ( R R ), для упрощения решения задачи можно изменение силы тока при изменении сопротивления заменить дифференциалом этой величины, то

есть воспользоваться приближенным соотношением					I ≈ dI . По оп-
′					тока (дифферен-
ределению dI = I (R)dR . Найдем производную силы
цируя закон Ома) I	′		U
		= − R2

12

Тогда для дифференциала силы тока имеем dI = − RU2 dR . Под-

ставляем числовые значения величин: dI = −2 10 −6 A

Ответ: ток в цепи уменьшился примерно на 2 10 −6 А.

Самостоятельно решить задачу:

Период

T

свободных незатухающих колебаний

колебательного

контура

выражается

формулой

Томсона

T = 2π

LC ,

где

L

- ин-

дуктивность,

C

- емкость колебательного контура. Найти

изме-

нение периода колебаний при увеличении

индуктивности

на

L

=

1 мкГн, если L=100

мкГн, C=500 пФ

(1

пФ=10-12

Ф,

1

мкГн=10-6

Гн).

Задача 3. Вычислить приближенно изменение площади квадра-

та S

со

стороной

l = 10 см

при увеличении

ее

длины

на

l

=

0,01 см.

Решение

S ≈ dS

Считаем, что

dS = (l 2 )′dl = 2 l dl

Зная, что

dl =

l , найдем изменение площади

dS = 2 l dl = 2 10 0.01 = 0.2

см2

Тогда

S ≈ dS

cм2

квадрата

увеличится

на

величину

Таким

образом,

площадь

S ≈ 0,2 см2

Задача 4. Найти частные и полный дифференциалы функции

Z = xy

Решение

Данная функция является функцией двух аргументов: x и y . По определению, полный дифференциал функции нескольких

переменных равен сумме частных дифференциалов: dZ = d x Z + d y Z ,

где dx Z = ∂∂Z dx ; x

d y Z = ∂∂Z dy y

Прежде всего найдем частные производные функции. При нахождении частной производной функции по одному из аргументов, все другие аргументы функции рассматриваются как постоянные величины. Тогда

∂Z ∂x

∂Z

∂y

=∂∂ x = x y

=∂∂ x = y y

1 ∂x

=

1

y ∂x

y

∂

(y

−1

)

1

x

x

−

= −

2

2

∂y

= x

y

y

Соответственно частные дифференциалы функции равны

13

d x Z =

∂Z

dx =

dx

;

y

∂x

d y Z =

∂Z

dy

= −x

dy

, а полный дифференциал

∂y

2

y

dZ =

dx

−

xdy

y

y2

Задача

5.

Радиус основания цилиндра R=50 см, а высота

h=120 см. Как

изменится объем цилиндра, если

R увеличить на

0,4 см,

а

высоту

h уменьшить на 0,5 см.

Объем цилиндра

V = πR2 h .

Решение

Если R и h получают приращения, то и объем цилиндра получит

приращение

V . Но

V ≈ dV .

dV =

∂V

dR +

∂V

dh

∂R

∂h

dR = R =0,4 см;

dh = h =-0,5 см.

В нашем случае

Найдем частные производные

∂V

=

∂

(πR2 h) = 2πRh = 2π 50 120 =12000π

∂R

∂R

∂V

=

∂

(πR2 h) = πR2 = 2500π

∂h

∂h

Тогда

∂V

∂V

dV =

dR

+

dh =12000π 0.4 + 2500π (−0.5)

=11147 см3

∂R

∂h

Следовательно, объем цилиндра увеличился на величину

V ≈11147 см3 .

Найти самостоятельно частные и полный дифференциалы функций:

	1)	Z = ln(x + y)	2) Z = sin(3x + 4 y)
	3)	Z = y ln x	3)	Z =	sin x
					cos y

Задачи для решения на практическом занятии.

	Найти дифференциалы функций:
1.	y = cos(x3 )				6.	y =	ex
	y = sin 2 x						x +1
2.					7.	y = cos 3		x
3.	y = x ln x				8.	y = x sin		x
4.	y =	3	x	4	9.	y =	x cos(x + 3)
5.	y = ecos x				10.		y = 3 x2 +3

14

Найти частные и полные дифференциалы функций двух переменных:

1. Z = x2 + y 2

5. Z = exy+x2

2. Z = e

xy

x

6.

Z = ln

+1

y

3. Z = x ln y

7. Z = ln(x3 − y4 )

4. Z = x2 + y 4

8.

P(T ,V ) =

RT

V

Решить задачи

4

1. Определить

изменение

объема

шара

V

=

πR3 , если

радиус

3

R

V ≈ dV .

R =2,5 м, а

= 0,1 м. Воспользоваться формулой

2. Количество

теплоты Q , выделяющейся в единице объема раство-

ра электролита

при

УВЧ-терапии,

описывается

формулой

Q = kσE 2t ,

где

σ - удельная

электропроводность,

k

- коэф-

фициент пропорциональности,

E -

напряженность

электриче-

ского поля между электродами терапевтического контура, t - время процедуры. Найти приближенно изменение количества теп-

ла (считая Q ≈ dQ ), если E = 200 В/м,		E	=-10 В/м; t = 10
мин,	t = 2 мин, k=1.
3. При	нагревании круга радиусом R =40 мм	его	площадь увеличи-

лась. Определить увеличение площади круга, если его радиус увеличился на R = 0.1 мм.

4.Из порошка анальгина спрессовали таблетки. Определить плот-

ность анальгина в таблетке по формуле ρ = π4dm2h . Вычислить

приближенно	изменение		плотности		таблетки, если	m =5,5
10 −4 г, m = 0,488 г;		h =	4,0	10 −3 см, h =0,54 см; d =0,4 10 −3
см; d =0,82 см.
5. Медный кубик,	ребро	которого		r = 5	см, подвергался	равномер-

ной шлифовке со всех сторон. Зная, что масса его уменьшилась

на 0,69 г, и считая плотность меди равной 8 г/см3 , определить приближенно насколько изменилось его ребро.

Т е м а 4

Неопределенный интеграл

Интегральное исчисление является составной частью математического анализа, и применяется при решении множества

15

задач из области физики, химии, биологии, а именно в тех случаях, когда по виду известной производной требуется найти вид самой функции.

Литература для подготовки к занятию по теме:

Ю.В.Морозов "Основы высшей математики и статистики", М., 1998, с.59-64, 66.

В процессе подготовки к практическому занятию по теме необходимо выполнить следующее:

1. Повторить следующие теоретические вопросы:

1)Понятие производной функции одной переменной.

2)Основные формулы дифференцирования.

3)Понятие дифференциала функции.

4)Понятие первообразной функции.

П. Изучить по указанной литературе следующие теоретические вопросы:

1)Понятие неопределенного интеграла.

2)Основные свойства неопределенного интеграла

3)Таблица основных интегралов.

4)Простейшие способы интегрирования: а) непосредственное интегрирование. б) интегрирование методом подставки.

Эталоны решения типовых задач и задачи для самоконтроля

Задача 1. Найти интеграл ∫(x2 − x − 2)dx

Решение В соответствии с одним из свойств неопределенного инте-

грала: интеграл алгебраической суммы нескольких функций равен алгебраической сумме неопределенных интегралов слагаемых. Поэтому

∫(x2 − x − 2)dx = ∫x2 dx − ∫xdx − ∫2dx

Используя другое свойство неопределенного интеграла, в соответствии с которым постоянный множитель подынтегральной функции можно выносить из под знака интеграла, получаем:

∫x2 dx − ∫xdx − ∫2dx = ∫x2 dx − ∫xdx − 2∫dx

Применяя формулу интегрирования степенной функции

xn+1

∫xn dx = n +1 +C

при нахождении каждого из трех интегралов в правой части, окончательно получаем:

∫(x2 − x − 2)dx = ∫x2 dx − ∫xdx − 2∫dx =	x3	−	x2	− 2x +C
3		2

Найти самостоятельно следующие интегралы:

1) ∫(2x2 + 5x − 6)dx

2) ∫(x +1)2 dx

16

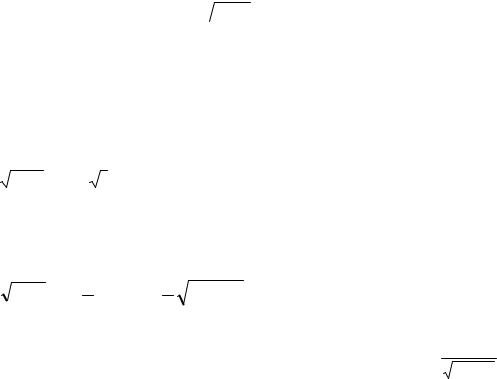
Задача 2. Найти ∫ x +1dx Решение

Введем новую переменную t = x +1 и выразим дифференциал dx через dt . В соответствии с определением дифференциала, имеем:

′

+1)

′

dx = dx , отсюда

dx = dt

dt = t dx = (x

Подставив t

в подынтегральное выражение, получим:

1

t

1

+1

3

∫ x +1dx = ∫ tdt = ∫t

dt =

2

+C =

2

t

+C

2

2

1

+1

3

2

Возвращаясь к первоначальной переменной x , окончательно получим:

∫	x +1dx =	2 t	3	+ C =	2	(x +1)3 + C
			2
		3			3

Найти самостоятельно следующий интеграл: ∫ 4dxx −3

Задача 3. Найти ∫cos 2 x sin xdx

Решение

Введем новую переменную t = cos x . Выразим

через dt . Для этого, дифференцируя выражение довательно получим

дифференциал dx cos x = t , после-

d (cos x) = dt ;	−sin x dx = dt ; dx = −				dt
					sin x
Подставляем в подынтегральное выражение
∫cos2 x sin xdx = −∫t		2 dt = −	t 3	+C
Возвращаясь		3				переменной x ,		окончательно
		к первоначальной
получим
∫cos2 x sin xdx = − cos3 x +C
	3
Найти самостоятельно следующие интегралы:
1) ∫cos 7xdx				2) ∫sin 2	x cos xdx
Задача	4.	Найти		∫enx dx ,	n		- постоянный	коэффициент,

n ≠ 0 .

Решение

Введем новую переменную t = nx , дифференцируем:

17

	d (nx) = dt ;					ndx = dt , отсюда			dx =	dt	. Тогда
										n
		dt		1			1
	∫enx dx = ∫et		=			∫et dt =		et +C
		n		n
							n

Возвращаясь к первоначальной переменной х, окончательно получим:

∫enx dx = 1n enx +C .

Найти самостоятельно следующие интегралы:

1) ∫e3x dx 2) ∫sin x ecos x dx

Задача 5. Скорость тела задана выражением V = (6t 2 + 2t) , где скорость измеряется в м/с, а время - в секундах. Найти зависимость координаты тела от времени (уравнение движения), если через 3 секунды после начала движения координата тела оказалась равной 60 м.

Решение

По определению скорости V = dxdt , тогда в нашем случае

	dx	= (6t 2 + 2t) .
	dt
			dx = (6t 2	+ 2t)dt .
		Отсюда
Интегрируя,				получаем:

x(t) = ∫(6t 2 + 2t)dt = 6∫t	2 dt + 2∫tdt = 6 t 3	+ 2 t 2 +C = 2t3 +t 2 +C .
	3	2	x(3) = 60 , получим:
Используя дополнительное условие задачи
x(3) = 2 33 +32 +C = 60 , откуда		C = −3 .
Таким образом, уравнение движения тела окончательно имеет
вид:
x(t) = 2t3 +t 2 −3 (м).
Решить самостоятельно следующую задачу:
Скорость точки	задана уравнением		V = (2t + 4) ) м/с. Найти

уравнение движения точки, если в начальный момент времени координата точки равна О.

Задача 6. Изменение численности микроорганизмов за едини-

цу времени задается формулой		dN	=100t 2 . Определить зависимость
		dt
			от времени, если при t = 0
количества микроорганизмов	N
N (0) =100 .
Решение

18

	Из формулы	dN	=100t 2	можно определить зависимость числа
		dt
					t 3
	микроорганизмов от времени			N(t) = ∫100t 2 dt =100		+C .
				3

Чтобы определить значение константы интегрирования C , нужно воспользоваться начальными условиями, т.е. N (0) =100 .

	N(0) =100	03	+C . Отсюда N (0) = C ,				C =100 .
	3							100
	Тогда получаем результат					N (t) =			t 3 +100 .
								3
	Следовательно,				количество		микроорганизмов увеличивается
	со временем			пропорционально		третьей степени времени, начиная
	со значения			N =100	в начальный момент времени.

Решить самостоятельно следующую задачу Сила, действующая на тело в направлении движения, изменя-

ется со временем по закону F = 2t (H).	Найти	скорость тела в
любой момент времени, зная, что в момент	t = 0	она была равна 1
м/с. Масса тела 3 кг.

Задачи для решения на практическом занятии:

1.

∫x5 dx

9. ∫ 5x −1dx

2.

∫(1 + 4x)(1 − 2x)dx

10.

∫sin(5x −1)dx

3.

∫

3x2

− 4x −6

dx

11.

∫sin

3

x cos xdx

x

2

dx

ctgx

4.

∫

12.

∫

dx

1 − x

sin 2 x

5.

∫

dx

13.

∫

dx

(1 + x)2

x ln x

6.

∫

2xdx

14.

∫

dx ln x

x2 +1

x

7.

∫x2

x3 +1dx

15.

∫tgx dx

8.

∫cos

2x −1

dx

16.

∫ex2

x dx

3

Решить задачи

движения

тела,

если

скорость

тела

1) Составить уравнение

V = t 2

− 2t + 5 (м/с),

а при t=0

тело

находилось в

точке

x = 0.

19

2) Скорость тела пропорциональна квадрату времени. Составить уравнение движения тела, если известно, что через 3 с ко-

ордината тела	x =18 см, а в начальный момент времени x0 = 0 .
3) Ток в цепи, содержащей конденсатор, изменяется с		тече-
нием времени	по закону I = I0 sin ωt , где I0 ,ω - постоянные	вели-

чины. Определить, как изменяется со временем заряд конденсатора, если в момент времени, когда ток максимален, заряд конденсатора равен нулю.

Т е м а 5

Определенный интеграл

Понятие определенного интеграла используют при решении практических задач, в частности, в задачах по вычислению площадей плоских фигур, расчету работы, производимой переменной силой и т.д.

Литература для подготовки к занятию по теме:

Ю.В.Морозов "Основы высшей математики". М., 1998, с.68-72, 74-76, 79-82.

В процессе подготовки к практическому занятию по теме необходимо выполнить:

1.Повторить следующие теоретические вопросы:

1)Основные свойства неопределенного интеграла.

2)Таблицу основных интегралов.

П. Изучить по указанной литературе следующие теоретические вопросы:

1) Понятие определенного интеграла (на примере нахождения площади криволиней-

ной трапеции).

2)Формула Ньютона-Лейбница для вычисления определенного интеграла.

3)Вычисление площади криволинейной трапеции с помощью определенного интеграла.

4)Вычисление работы переменной силы с помощью определенного интеграла. Эталоны решения типовых задач и задачи для самоконтроля.

Задача 1. Вычислить определенный интеграл: ∫2

x2 dx

Решение:

1

b

ba = F(b) − F(a) ,

По формуле Ньютона-Лейбница ∫ f (x)dx = F(x)

a

где F(x) - первообразная функция для подынтегральной функции f (x) .

Поскольку простейшей первообразной для функции f (x) = x2 является

F(x) =

x3

, в дан-

3

ном случае имеем: ∫2

x2 dx =

x3

12 =

23

−

13

=

8

−

1

=

7

1

3

3

3

3

3

3

Вычислить самостоятельно определенные интегралы:

π

1. ∫2 sin xdx

3. ∫3

dx

x

0

1

20