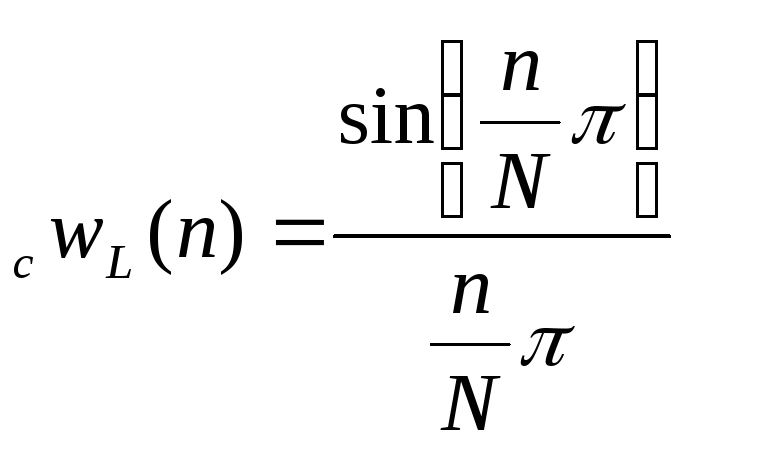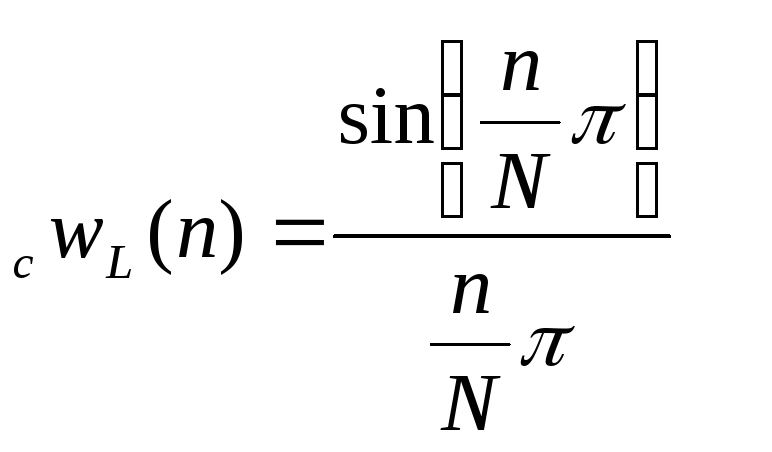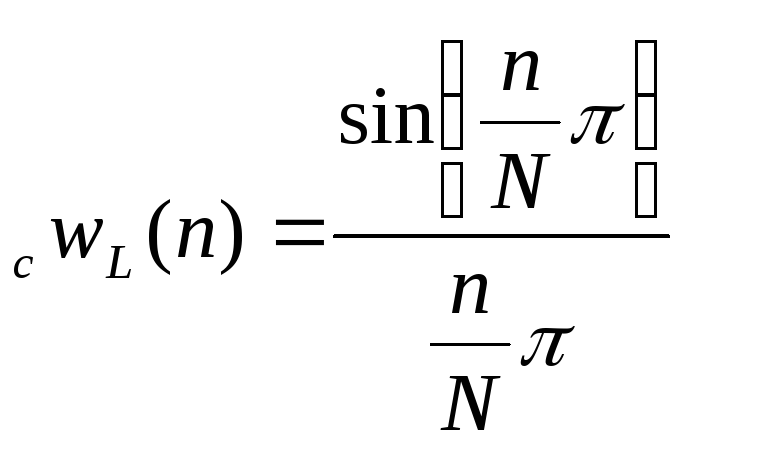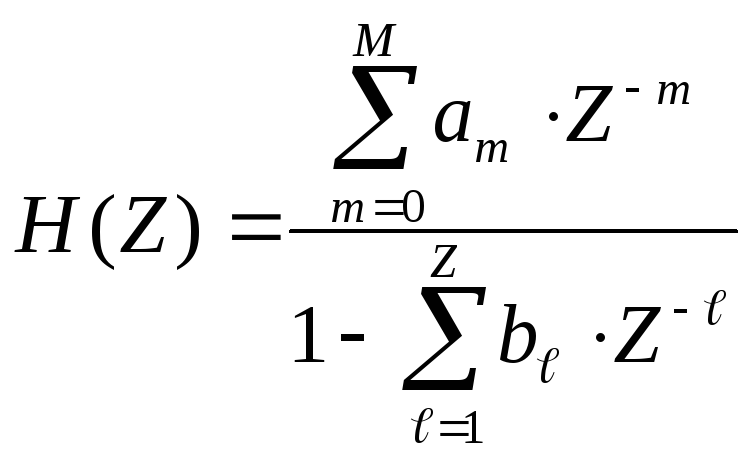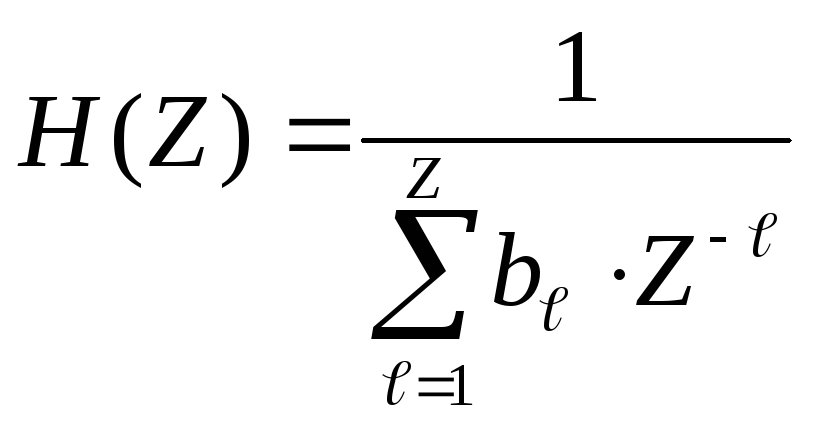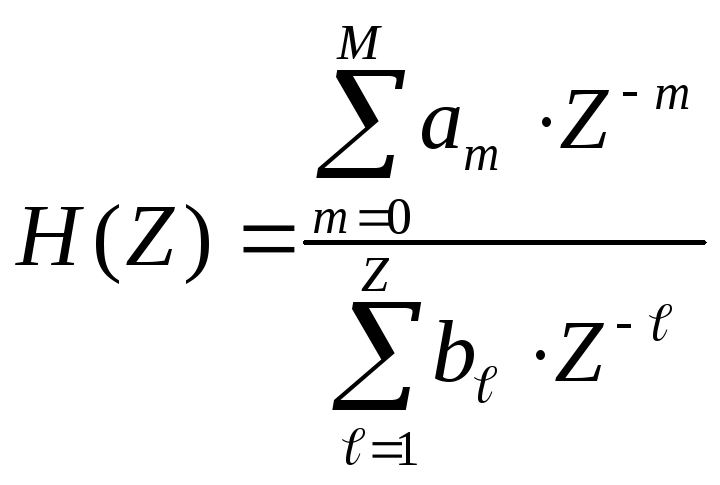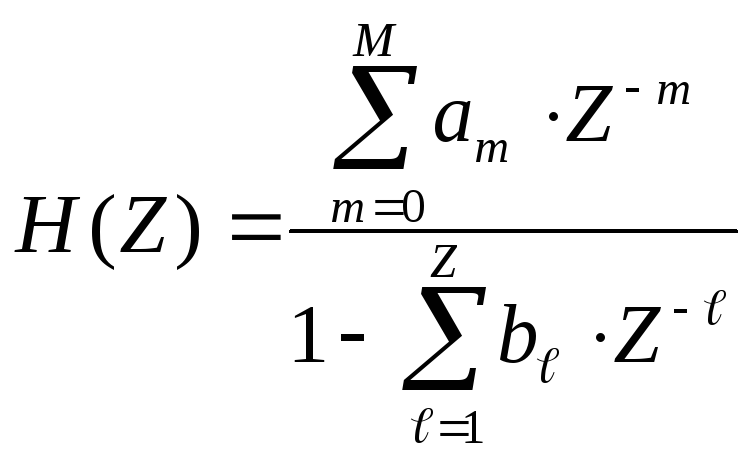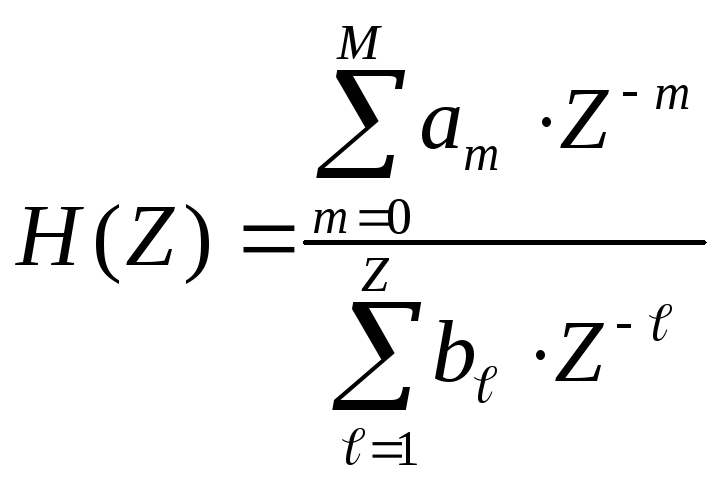- •1. Основи теорії кіл Розділ 1.1. Основні поняття і визначення
- •Розділ1.2. Кола постійного струму
- •Розділ1.3 Однофазні кола змінного струму
- •Розділ1.4. Трифазні кола змінного струму
- •Розділ1.5. Перехідні процеси в електричних колах
- •2. Аналогові електронні пристрої
- •Розділ2.2.
- •Розділ2.3
- •3. Радіоелектронні системи Розділ 3.1
- •Розділ3.2
- •Розділ3.3
- •Розділ3.4
- •Розділ3.5
- •4. Цифрове оброблення сигналів Розділ 4.1.
- •Розділ 4.2.
- •Розділ 4.3
- •Розділ4.4
- •Розділ4.5
- •5. Сигнали та процеси в радіотехніці6. Сигнали та процеси в радіотехніці Розділ 5.1.
- •Розділ 6.2
- •Розділ 6.3.
- •Розділ 5.4.
- •Розділ 5.5.
Розділ 4.2.
|
1 |
2 |
7 | |||
|
|
Яким математичним рівнянням описують дискретну лінійну згортку
|
a. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
Z-перетворення імпульсної характеристики системи, називається
|
в. | |||
|
a) Імпульсною характеристикою |
б) Частотною характеристикою |
в) Функцією передачі |
г) Фазова характеристика | ||
|
|
Пряме Z– перетворення X(Z) послідовності X(nT) визначається формулою:
|
б. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
Зворотнє Z– перетворення визначається формулою:
|
в. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
Z-образ x(z) (причинна система) дискретної послідовності x(nT)={1,2,0,-2}:
|
a. | |||
|
a) x(z) = z0+2z-1-2z-3 | |||||
|
б) x(z) = -2z0+2z2+z3 | |||||
|
в) x(z) = z1+2z2-2z4 | |||||
|
г) x(z) = -2z-1+2z-3+z-4 | |||||
|
|
Z-образ x(z) (непричинна система) дискретної послідовності x(nT)={1,2,0,-2}:
|
б. | |||
|
a) x(z) = -2z0+2z2+z3 | |||||
|
б) x(z) = z0+2z1-2z3 | |||||
|
в) x(z) = z1+2z2-2z4 | |||||
|
г) x(z) = -2z-1+2z-3+z-4 | |||||
|
|
Z-образ функції δ(n) одиничний імпульс
x (nT)= 0, n>0:
|
a. | |||
|
a) x (z)= 1 |
б) x (z)= |
в) x (z)= |
г) x (z)= | ||
|
|
Z x (nT)= 1, n 0 0, n<0: |
в. | |||
|
a) x (z)= 1 |
б) x (z)= |
в) x (z)= |
г) x (z)= | ||
|
|
Z-образ функції x (nT)= (-1) n меандр
|
г. | |||
|
a)
x (z)= |
б) x (z)= 1 |
в) x
(z)= |
г)
x (z)= | ||
|
|
Z-образ функції x (nT)= an
|
a. | |||
|
a)
x (z)= |
б)
x (z)= |
в) x (z)= 1 |
г)
x (z)= | ||
|
|
Пряме перетворення Фур’є послідовності X(nT) визначається формулою:
|
б. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
Зворотнє перетворення Фур’є визначається формулою:
|
a. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
Пряме дискретне перетворення Фур’є послідовності X(nT) визначається формулою:
|
в. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
Зворотнє дискретне перетворення Фур’є визначається формулою:
|
a. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
ДПФ є окремим випадком Z –перетворення при умові:
|
г. | |||
|
a) Z= 1 |
б) Z= iwT |
в) Z=0 |
г) Z= eiwT | ||
Розділ 4.3
|
1 |
2 |
7 | |||
|
|
Для ДПФ перша синусоїда спектру має частоту, яка:
|
a. | |||
|
a) Співпадає з періодом самого вихідного сигналу |
б) Дорівнює нулю |
в) Дорівнює половині частоти дискретизації |
г) Необмежена | ||
|
|
Для ДПФ сама висока складова спектру має частоту:
|
в. | |||
|
a) Співпадає з періодом самого вихідного сигналу |
б) Дорівнює нулю |
в) Дорівнює половині частоти дискретизації |
г) Необмежена | ||
|
|
Для обчислення N–точечного ДПФ необхідно виконати наступну кількість операцій комплексного множення і додавання:
|
б. | |||
|
a) N2 i N |
б) N2 i N(N-1) |
в) N i N |
г) N i N2(N-1) | ||
|
|
БПФ з проріджуванням за часом дозволяє получити виграш у обчислювальних операціях , раз:
|
б. | |||
|
a)
|
б)
|
в) N2 |
г) N(N-1) | ||
|
|
Прямокутне
вагове вікно для компенсації явища
Гібсона
|
a. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
Вагове вікно Хеммінга для компенсації явища Гібсона
|
б. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
Вагове вікно Хеммінга для компенсації явища Гібсона .
|
в. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
Вагове
вікно Ланцоша для компенсації явища
Гібсона
|
г. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
В загальному виді цифрові фільтри представлені виразом:
|
в. | |||
|
a)
y(k) =
| |||||
|
б)
y(k) =
| |||||
|
в)
y(k) =
| |||||
|
г)
y(k) =
| |||||
|
|
В загальному виді цифрові нерекурсивні фільтри представлені виразом:
|
a. | |||
|
a)
y(nT) = | |||||
|
б)
y(nT) =
| |||||
|
в) y(nT)
= | |||||
|
г)
y(nT) = | |||||
|
|
В загальному виді цифрові рекурсивні фільтри представлені виразом:
|
б. | |||
|
a)
y(nT) = | |||||
|
б)
y(nT) = | |||||
|
в) y(nT)
= | |||||
|
г)
y(nT) = | |||||
|
|
Загальний вид передаточної функції рекурсивного цифрового фільтра
|
б. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
Загальний вид передаточної функції нерекурсивного цифрового фільтра
|
a. | |||
|
a)
| |||||
|
б)
| |||||
|
в)
| |||||
|
г)
| |||||
|
|
Якщо передаточна функція фільтра представляє собою не скорочуваний дріб, то для його стійкості необхідно і достатньо виконання умови
|
в. | |||
|
a) |zl|>1; l=1,2,3,…,M-1 |
б) |zl|<0; l=1,2,3,…,M-1 |
в) |zl|<1; l=1,2,3,…,M-1 |
г) |zl|>0; l=1,2,3,…,M-1 | ||
|
|
Формула для розрахунків коефіцієнтів ФНЧ з нормованою граничною частотою:
|
г. | |||
|
a)
ак=а-к= | |||||
|
б)
ак=а-к= | |||||
|
в)
ак=а-к= | |||||
|
г)
ак=а-к= | |||||

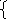 1, n=0
1, n=0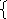 -образ
функції Одиничний стрибок
-образ
функції Одиничний стрибок