математика / Matematika_Kursovaya_rabota

21

Таким образом, из независимости случайных величин следует их некоррелированность, причем из некоррелированности двух случайных величин еще не следует их независимость. Если ρxy = 0, это означает только отсутствие линейной связи между случайными величинами, любой другой вид связи при этом может присутствовать. Из коррелированности двух случайных величин следует их зависимость, но из зависимости не следует коррелированность.

Если совместным распределением вероятностей величин Х и У служит нормальное распределение, то имеет место нормальная корреляция, которая всегда линейна. При нормальной корреляции из некоррелированности случайных величин Х и Y вытекает их независимость.

1.6.3 Условное математическое ожидание. Регрессия

Наиболее важной характеристикой для описания условных законов распределения является условное математическое ожидание.

Условным математическим ожиданием дискретной случайной величины X при Y = y (y - определенное значение случайной величины Y)

называется сумма произведений возможных значений X на их условные вероятности:

n	y).
M [X Y = y]= ∑xi p(xi		(1.49)
i=1

Для непрерывных случайных величин

M [X Y = y]=	+∞
	∫xf (x y)dx,	(1.50)

−∞

где f(x/y) – условная плотность распределения случайной величины X при

Y=y.

Аналогично условным математическим ожиданием дискретной случайной величины Y при X = x называется сумма произведений возможных значений Y на их условные вероятности:

m	x).
M [Y X = x]= ∑ y j p(y j		(1.51)
j =1
Для непрерывных случайных величин
M [Y X = x]= ∞∫ yf (y x)dx ,		(1.52)
−∞
где f(x/y) – условная плотность распределения случайной величины Y при

X=x.

Условное математическое ожидание случайной величины X при Y = y,
то есть M [X Y = y]= x( y ), есть функция от y, которая называется функцией
регрессии X по Y, аналогично M [Y X = x]= y( x )	называется функцией
регрессии Y по X. Уравнения
M [X Y = y]= x( y ),	(1.53)

22
M [Y X = x]= y( x )	(1.54)

называются уравнениями регрессии соответственно X по Y и Y по X. Линии,

определяемые уравнениями (1.53) и (1.54), называются линиями регрессии

(кривыми регрессии).

Важное свойство линий регрессии сформулировано в следующей теореме.

Теорема 8. Для произвольной функции u(x) справедливо неравенство

M [(Y −u( x ))2 ]≥ M [(Y − y(x))2 ],

(1.55)

где M [Y X = x]= y( x ) уравнение линии регрессии, то есть линия регрессии M [Y X = x]= y( x ) минимизирует среднюю квадратическую погрешность прогноза величины Y по X.

23

2 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Целью математической статистики является разработка методов получения, описания и обработки опытных данных для изучения закономерностей случайных массовых явлений.

Основные задачи математической статистики:

–оценить неизвестные числовые характеристики случайной величины (математическое ожидание, дисперсия и тому подобное) на основе независимо полученных значений этой случайной величины (выборки);

–выдвинуть и проверить статистические гипотезы (о предполагаемом неизвестном законе распределения случайной величины, о равенстве двух неизвестных математических ожиданий, о принадлежности двух выборок одной и той же случайной величине и т.п.) на основе выборки;

–построить математические модели зависимости составляющих системы случайных величин и определить адекватность этих математических моделей на основе k-мерной выборки.

2.1 ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ И ВЫБОРКА

Пусть требуется изучить совокупность однородных объектов относительно некоторого признака, характеризующего эти объекты. На практике для этого случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.

Случайной выборкой (или просто выборкой) называется совокупность случайно отобранных объектов. Число объектов выборки называется ее объемом. Совокупность объектов, из которых производится выборка,

называется генеральной совокупностью.

Пусть случайная величина Х – некоторый признак, характеризующий исследуемые объекты, а х1, х2, …, хn .– результаты наблюдений (измерений) этой случайной величины, полученные в ходе выполнения n независимых однородных опытов.

Наблюдаемые значения х1, х2, …, хn случайной величины Х называются

значениями выборки или вариантами, а последовательность вариант,

записанных в порядке возрастания или убывания, – вариационным рядом. Случайная выборка является математической моделью независимых

измерений, проводимых в одинаковых условиях.

Выборка является основной, а зачастую единственной информацией о случайной величине Х. Исследование случайных величин и их характеристик с использованием выборки называют выборочным методом. Характеристики величины Х, определенные по выборке, называют эмпирическими. При этом объективно существующие характеристики случайных величин называют

теоретическими.

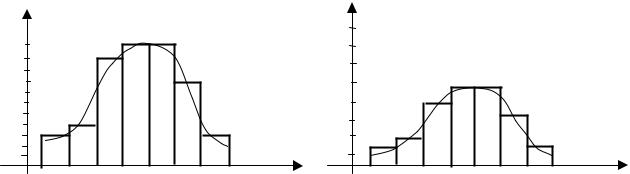
24

2.2 ГИСТОГРАММА

Для оценки закона распределения используют эмпирическую функцию распределения и эмпирическую плотность, называемую гистограммой.

Для построения гистограммы весь диапазон изменения значений выборки разбивается на интервалы (необязательно равновеликие) длиной hi и определяется количество вариант ni, попавших в каждый из интервалов (при этом удобно представить выборку в виде вариационного ряда). Величина ni называется эмпирической частотой попадания в интервал.

Гистограммой частот (относительных частот) называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат выбранные интервалы длиной hi , а высоты равны отношению ni / hi (pi*/ hi , где pi*= ni / n – относительная частота значения xi).

Замечания

1Площадь гистограммы относительных частот равна единице.

2Площадь гистограммы частот равна n.

3Гистограмма частот и относительных частот отличаются "сжатием" второй из них в n раз по вертикали.

Гистограммы	частот и относительных частот приведены на
рисунках 2.1, 2.2.
ni/hi	pi*/ hi

x1 x2 x3	xi xi+1	xn	x	x1 x2 x3	xi xi+1	xn	x
Рисунок 2.1				Рисунок 2.2

Для удобства оценки вида плотности распределения обычно гистограмму мысленно сглаживают плавной кривой.

θ~ = f(X1, X2, …, Xn).

25

2.3 ТОЧЕЧНЫЕ ОЦЕНКИ ЧИСЛОВЫХ ХАРАКТЕРИСТИК. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К НИМ

Для оценки неизвестного параметра распределения по выборке, значения х1, х2, …, хn,, полученные в результате n наблюдений, рассматриваются как независимые случайные величины X1, X2, …, Xn, каждая из которых имеет тот же закон распределения , что и сама случайная величина X.

Статистической оценкой θ~ неизвестного параметра θ называется функция f(X1, X2, …, Xn) от наблюдаемых случайных величин X1, X2, …, Xn, то есть

Так как X1, X2, …, Xn – случайные величины, то и оценка θ~ является случайной величиной и меняется от выборки к выборке. Оценки числовых

характеристик делятся на точечные и интервальные. ~
Точечной называется статистическая оценка θ , которая выражается
одним числом.
К точечным оценкам предъявляются следующие требования:
-	несмещенность;
-	эффективность;
-	состоятельность.
Оценка θ~		параметра θ	называется несмещенной, если	ее
математическое ожидание равно оцениваемому параметру, то есть М[θ~				]=θ.
В противном случае оценка называется смещенной.
Очевидно, что если оценка θ~			дает приближенное значение параметра θ
с избытком, то М[θ~		] >θ , а если θ~ дает оценку с недостатком, то М[θ~ ] <θ.

Таким образом, требование несмещенности гарантирует отсутствие систематических ошибок при оценивании.

Однако несмещенная оценка θ~ может давать значения сильно

рассеянные вокруг своего среднего значения, то есть дисперсия D[θ~ ] может быть значительной. В этом случае найденная по данным выборки оценка может оказаться сильно удаленной от оцениваемого параметра θ. Поэтому

требование наименьшей дисперсии θ~ исключает возможность допустить большую ошибку при оценивании.

Несмещенная оценка θ~ параметра θ называется эффективной, если она имеет наименьшую дисперсию по сравнению с другими несмещенными оценками величины θ, вычисленными по выборкам одного и того же объема n.

Оценка θ~ называется состоятельной, если при неограниченном увеличении объема выборки (n → ∞) вероятность ее отклонения от θ стремиться к 1, то есть

26

lim P(θ~ −θ <ε) =1,

n→∞

где ε – любое наперед заданное сколь угодно малое положительное число. Для данного соотношения θ~ и θ часто используется термин:

θ~ сходится по вероятности к θ.

Увеличение объема выборки при использование состоятельных оценок уменьшает вероятность значительных ошибок при оценивании.

Приведем точечные оценки основных числовых характеристик случайных величин, удовлетворяющие перечисленным выше требованиям:

~	1 n
- выборочная средняя: M [X ]= xв =		i∑=1xi		;
	n				1
			~	2			n	2
- исправленная выборочная дисперсия:			D[X ]= Sx		=		i∑=1( xi − xв )		;
						n −1

-выборочное среднее квадратическое отклонение: σ~[X ]= Sx = Sx2 ;

-выборочный коэффициент корреляции:

~ r

- ρxy = xy

- выборочная асимметрия:

	n
=	∑(xi − xв )( yi − yв )					;
	i=1
	n			n
	∑(xi		− xв )2 ∑( yi − yв )2
	i=1			i=1
				n
~				∑(xi − xв )3
				i=1
As = as		=							;
			n (	1		3
					∑(xi − xв )2 ) 2
					n

n −1 i=1

		n			− xв )4
~		∑( xi
		i=1
- выборочный эксцесс: Ek = ek =						– 3.
		1		n
	n (			∑( xi − xв )2 )2
		n −
			1i=1

2.4ИНТЕРВАЛЬНЫЕ ОЦЕНКИ. ДОВЕРИТЕЛЬНАЯ ВЕРОЯТНОСТЬ И

ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ. ДОВЕРИТЕЛЬНЫЙ ИНТЕРВАЛ ДЛЯ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ

Приведенные выше точечные оценки числовых характеристик, несмотря на широкое использование, имеют большой недостаток. Этот недостаток заключается в том, что, во-первых, для выборки малого объема точечная оценка может значительно отличаться от оцениваемого параметра, во-вторых, точечная оценка не несет информации о том, как она соотносится со значением оцениваемого параметра. Гораздо больше информации об оцениваемом параметре несут интервальные оценки.

Интервальной называется оценка, которая определяется двумя числами

– концами интервала, покрывающего оцениваемый параметр θ.

27

Очевидно, что по выборке ограниченного объема нельзя построить интервальную оценку, являющуюся достоверной. Можно говорить только о том, что интервальная оценка с некоторой вероятностью верна. Такая вероятность называется доверительной вероятностью или надежностью оценки.

Доверительной вероятностью (надежностью) оценки θ называется вероятность γ, с которой интервальная оценка накрывает оцениваемый параметр θ.

Обычно в инженерной практике доверительная вероятность (надежность) оценки задается наперед, после чего определяется интервал, соответствующий данной вероятности (доверительный интервал). Обычно доверительную вероятность задают близкой к единице, например, равной 0,9, 0,95 или 0,99.

Доверительным интервалом, называется интервал, определенный по выборке, который с заданной надежностью γ накрывает неизвестный параметр θ.

Рассмотрим построение доверительного интервала для неизвестного математического ожидания a нормально распределенной случайной величины Х по выборке объема n. Рассмотрим два случая.

1 Пусть известно среднее квадратическое отклонение σ[Х] = σ, тогда доверительный интервал для неизвестного математического ожидания a нормально распределенной случайной величины Х имеет вид:

		xв – t	σ	< a < xв + t	σ	,	(2.1)
			n		n
где δ = t	σ	– точность оценки,
	n						Φ(t), при
t –
	значение аргумента		нормированной		функции Лапласа

котором Φ(t)= γ2 .

2 Пусть среднее квадратическое отклонение σ[Х] = σ неизвестно. В этом случае доверительный интервал для неизвестного математического ожидания a нормально распределенной случайной величины Х имеет вид:

xв −t(γ ,n−1) Sx	< a < xв + t(γ ,n−1)	Sx	,	(2.2)
n		n
где Sx – выборочное среднее квадратическое отклонение,
t(γ ,n−1) – критическое значение распределения Стьюдента,				определяемое

по таблице распределения Стьюдента в зависимости от надежности оценки γ и числа степеней свободы τ = (n – 1).

В этом случае точность оценки

δ = t(γ ,n−1) Snx .

28

2.5 ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. ОШИБКИ ПЕРВОГО И ВТОРОГО РОДА. УРОВЕНЬ ЗНАЧИМОСТИ

Как отмечалось, одной из основных задач математической статистики является проверка статистических гипотез.

Статистической гипотезой называется любое предположение о виде неизвестного закона распределения или о параметрах известных распределений, то есть относящееся к характеристикам случайных величин.

Например, статистическими гипотезами являются следующие предположения: средний расход бензина для автомобиля данного типа на 100 км пути равен 12 литрам; время безотказной работы двигателя автомобиля распределено по показательному закону.

Нулевой (основной) гипотезой H0 называется проверяемая (выдвинутая) гипотеза. Конкурирующей (альтернативной) гипотезой H1

называется гипотеза, которая противоречит основной.

Простой гипотезой называется гипотеза, которая содержит только одно предположение. Гипотеза, которая состоит из конечного или бесконечного числа простых гипотез, называется сложной.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Для принятия решения о справедливости гипотезы Н0 или Н1 выбираются специальные критерии. Поскольку речь идет о статистических методах исследования, всегда существует возможность допустить ошибку при принятии решения. При этом возможны следующие ситуации:

-гипотеза Н0 верна, в результате проверки гипотеза Н0 принята;

-гипотеза Н0 верна, в результате проверки гипотеза Н0 отвергнута (принята альтернативная гипотеза Н1);

-гипотеза Н0 не верна, в результате проверки гипотеза Н0 принята;

-гипотеза Н0 не верна, в результате проверки гипотеза Н0 отвергнута (принята альтернативная гипотеза Н1). Схема различных ситуаций, возникающих при принятии решения, приведена на рисунке 2.3.

В действительности				В результате проверки
справедлива гипотеза				принята гипотеза
H0			Р00		Н0
				Р10
				Р01
H1					H1
			Р11

Рисунок 2.3

29

Если в результате проверки гипотеза Н0 отвергается (принимается гипотеза Н1), хотя на самом деле Н0 верна, то допускается ошибка, называемая ошибкой первого рода.

Вероятность Р01 ошибки первого рода, – отвергнуть гипотезу Н0, когда она верна, обозначается через α ( α=1-γ) и называется уровнем значимости

(критерия).

Если в результате проверки принята гипотеза Н0, хотя на самом деле верна гипотеза Н1, допускается ошибка второго рода. Вероятность Р10 ошибки второго рода обозначают через β.

Вероятность 1–β не допустить ошибку второго рода, то есть отвергнуть гипотезу Н0 , когда она неверна, называется мощностью критерия.

При проверке статистических гипотез исследователь наперед задает допустимую вероятность ошибки первого рода, то есть величину α, на которой проверяется гипотеза Н0.

Выбор уровня значимости определяется последствиями ошибки первого рода.

Заметим, что одновременно уменьшить вероятность ошибок первого и второго рода при данном объеме выборки невозможно (при уменьшении α увеличивается β и наоборот). Единственный способ уменьшить вероятности обеих этих ошибок – увеличить объем выборки.

2.6 КРИТЕРИЙ СОГЛАСИЯ. КРИТИЧЕСКАЯ ОБЛАСТЬ И ОБЛАСТЬ ПРИНЯТИЯ ГИПОТЕЗЫ

Для проверки гипотезы Н0 необходимо выбрать критерий, на основе которого принимается решение о справедливости данной гипотезы.

Критерием (статистическим критерием, статистикой) называется случайная величина R с известным точным или приближенным законом распределения, которая строится по результатам выборки и предназначенная для проверки нулевой гипотезы.

В связи с тем, что критерий R предназначен для определения того, насколько выдвинутая гипотеза согласуется с выборкой, его часто называют критерием согласия. Следует подчеркнуть, что применение статистических критериев не дает однозначный ответ на вопрос о справедливости гипотезы Н0. Можно лишь утверждать, что имеющиеся эмпирические данные не противоречат (или противоречат) рассматриваемой гипотезе.

Значение критерия, вычисленное по выборке, называется наблюдаемым значением критерия Rнабл.

После выбора критерия согласия множество всех его значений разбивают на два непересекающихся подмножества. Одно из них содержит значения, при которых нулевая гипотеза Н0 отвергается, другое – при которых она принимается.

Критической областью называется множество значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотезы

30

(областью допустимых значений) называется множество значений критерия, при которых нулевую гипотезу принимают.

Критическая область определяет область, в которую случайная величина R, соответствующая критерию, попадает с вероятностью α, а область принятия гипотезы – область, в которую случайная величина R попадает с вероятностью 1–α.

Точки Rкр, разделяющие критическую область и область принятия гипотезы, называются критическими точками (значениями).

Значения критических точек для распределений, которым подчиняются наиболее часто употребляемые критерии, табулированы в зависимости от величин α, τ.

Основной принцип использования критерия согласия при проверке статистических гипотез сводится к следующему:

-по результатам выборки определяется наблюдаемое значение критерия Rнабл;

-находится критическая точка Rкр в зависимости от значений α и τ;

-отвергается нулевая гипотеза Н0, если Rнабл принадлежит критической области, в противном случае считается, что гипотеза согласуется с выборкой и отвергать ее нет оснований.

Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.

Правосторонней называется критическая область, определяемая

неравенством R>Rкр, где Rкр>0.

Левосторонней называется критическая область, определяемая

неравенством R<Rкр, где Rкр<0.

Двусторонней называется критическая область, определяемая

неравенствами R<R1, R>R2, где R2>R1. Если критические точки симметричны относительно нуля, двусторонняя критическая область определяется

неравенствами | R | > Rкр.

Критическую область выбирают так, чтобы вероятность попадания в нее критерия R была минимальной и равной α, если верна нулевая гипотеза Н0, и максимальной в противоположном случае. То есть критическая область должна быть такой, чтобы при заданном уровне значимости α мощность критерия 1–β была максимальной. В зависимости от вида конкурирующей гипотезы Н1 выбирают правостороннюю, левостороннюю или двустороннюю критическую область, для определения которых достаточно найти критическую точку Rкр. Границы критических областей Rкр при заданном уровне значимости α определяются соответственно из соотношений:

для правосторонней критической области

Р(R > Rкр) = α,

для левосторонней критической области

Р(R < Rкр) = α,