математика / Matematika_Kursovaya_rabota

РЯЗАНСКИЙ ВОЕННЫЙ АВТОМОБИЛЬНЫЙ ИНСТИТУТ им. ГЕНЕРАЛА АРМИИ В.П. ДУБЫНИНА

Л.Б. Михеева

МАТЕМАТИКА МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Учебно-методическое пособие по курсовой работе

Рязань 2007

2

УДК 519.2 ББК 22.17

М69

Рецензенты:

Кафедра математики Рязанской государственной сельскохозяйственной академии им. Костычева

Михеева Л.Б.

М69 Математика. Математическая статистика [Текст]: учеб.–метод. пособие по курсовой работе / Л.Б. Михеева – Рязань: РВАИ, 2007.– 67с.

Учебно-методическое пособие разработано в соответствии с программой и тематическим планом дисциплины «Математика».

Пособие предназначено для использования курсантами при выполнении расчетов курсовой работы, а также может быть использовано преподавателями при проведении занятий по темам математической статистики и адъюнктами при выполнении статистической обработки экспериментальных данных.

Пособие разработано доцентом Л.Б. Михеевой, обсуждено и одобрено на заседании кафедры 27.03.2007 протокол № 8.

УДК 519.2 ББК 22.17 РВАИ, 2007

3

СОДЕРЖАНИЕ	4
Введение ……………………………………………………………………....
1 Некоторые сведения из теории вероятностей ..………………...….....	6

1.1Различные определения вероятности …………………………….….. 6

1.2Дискретные и непрерывные случайные величины ………………….. 7

1.3Закон распределения. Функция распределения и плотность вероятности, их взаимосвязь и свойства ……………………............... 8

1.4Числовые характеристики случайных величин…………………….... 9

1.5Основные законы распределения вероятностей непрерывных

случайных величин ………………..…………………………............... 11

1.5.1Равномерный закон распределения ………………...………..…......... 11

1.5.2Показательный закон распределения …………………....................... 12

1.5.3Нормальный закон распределения …………………………………... 13

1.5.4Распределение χ2 …………………………...………………….………. 14

1.5.5Распределение Стьюдента ……………………………...…..……….... 15

1.5.6Распределение Фишера–Снедекора ………………………..……........ 16

1.6	Системы случайных величин. Функция регрессии ………....….…….	17
1.6.1	Совместное распределение вероятностей и распределение	17
	вероятностей каждой из составляющих …………….……………..…
1.6.2 Коррелированность и зависимость случайных величин ……….…....		19
1.6.3 Условное математическое ожидание. Регрессия ……………….....…		21
2	Некоторые сведения из математической статистики ………………..	23

2.1Генеральная совокупность и выборка ………………………….…...... 23

2.2Гистограмма …………………………………………………….……... 24

2.3Точечные оценки числовых характеристик. Требования,

предъявляемые к ним …………………………….……………………. 25

2.4Интервальные оценки. Доверительная вероятность и доверительный интервал. Доверительный интервал для

математического ожидания ………………………………………….... 26

2.5Проверка статистических гипотез. Ошибки первого и второго рода.

Уровень значимости ………………………………….……………..… 28

2.6Критерий согласия. Критическая область и область принятия гипотезы ……..………………………………....………….………….... 29

2.7Критерий χ2 Пирсона и его применение ……………………….…...... 31

2.8Элементы теории регрессии …………………….……………….......... 33 2.8.1 Функциональная и стохастическая зависимость величин ………….. 33 2.8.2 Модели функции регрессии ………………………………................... 34

2.9Корреляционный анализ ……………………………………………..... 35

2.10Основы вычислительного эксперимента …………………………...... 36

2.11Метод наименьших квадратов ……………………………................... 37

2.12Проверка адекватности регрессионной модели ……………............... 38 3 Пример выполнения курсовой работы ...……………………………... 41 Приложение А Пример оформления курсовой работы .…..………………. 57 Приложение Б Математико–статистические таблицы ……………...……... 60

4

ВВЕДЕНИЕ

Пособие предназначено для оказания помощи курсантам в выполнении курсовой работы по математике. Может быть использовано как на занятиях по дисциплине «Математика» при изучении тем курсовой работы, так и во время самостоятельных подготовок при изучении теоретических вопросов или выполнении расчетной части курсовой работы.

Пособие содержит три раздела и приложения. В первом разделе кратко изложены необходимые сведения из теории вероятностей. Во втором разделе рассмотрены основные вопросы математической статистики, необходимые для выполнения заданий курсовой работы. В третьем разделе приведены подробные примеры решения задач курсовой работы, а также методические указания и рекомендации по их выполнению.

Задание курсовой работы состоит из двух задач. Первая задача заключается в выдвижении и проверки гипотезы о законе распределения случайной величины с помощью критерия Пирсона. Вторая задача курсовой работы направлена на проведение корреляционного и регрессионного анализа при исследовании системы двух случайных величин.

В приложениях приведен образец оформления курсовой работы (приложение А) и таблицы значений функции Лапласа и критических точек основных законов распределений, необходимые для проведения расчетов (приложение Б).

При выполнении заданий курсовой работы и для подготовки к ее защите рекомендуется изучить вопросы из предлагаемого списка.

Вопросы для подготовки к защите курсовой работы по математике

1Различные определения вероятности события.

2Дискретные и непрерывные случайные величины (определения, примеры).

3Закон распределения вероятностей. Функция распределения и плотность вероятностей, их взаимосвязь и свойства.

4Числовые характеристики случайных величин (М[Х], D[Х], σ[Х]).

5Нормальный закон распределения вероятностей (F(х), f(х), Р(α<X<β), числовые характеристики).

6Равномерный закон распределения вероятностей (F(х), f(х), Р(α<X<β), числовые характеристики).

7Показательный закон распределения вероятностей (F(х), f(х), Р(α<X<β), числовые характеристики).

8Система случайных величин. Условное математическое ожидание. Регрессия.

9Коэффициент корреляции, его свойства. Взаимосвязь коррелированности и зависимости случайных величин.

5

10Предмет математической статистики. Генеральная совокупность и выборка. Гистограмма.

11Точечные оценки числовых характеристик. Требования, предъявленные к оценкам.

12Интервальные оценки. Доверительная вероятность и доверительный интервал. Доверительный интервал для математического ожидания.

13Статистический критерий. Критическая область и область принятия гипотезы. Критическое значение. Понятия о проверке статистических гипотез.

14Ошибки первого и второго рода. Уровень значимости. Мощность критерия.

15Критерии χ2 Пирсона и его применение.

16Функциональная и стохастическая зависимость. Регрессионные модели.

17Корреляционный анализ. (Оценка коэффициента корреляции. Проверка гипотезы о некоррелированности случайных величин).

18Метод наименьших квадратов.

19Проверка адекватности регрессионной модели.

6

1 НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ

1.1 РАЗЛИЧНЫЕ ОПРЕДЕЛЕНИЯ ВЕРОЯТНОСТИ

Любая наука содержит ряд основных понятий, на которых она базируется. Такими понятиями в теории вероятностей являются, в частности, опыт, исход опыта, событие.

Под опытом (экспериментом, испытанием) понимается выполнение некоторой совокупности условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат. Исходом опыта называется любой факт, который в результате опыта произошел.

Случайным событием (или просто событием) называется любой факт,

который в результате опыта может произойти, а может не произойти. Любое случайное событие обладает некоторой степенью возможности.

Для сравнения событий между собой по степени их возможности с каждым из них связывают некоторое число, которое тем больше, чем более возможно событие. Это число называется вероятностью события. Вероятность – одно из основных понятий теории вероятностей. Существует несколько определений этого понятия.

Статистическое определение вероятности

Предположим, что произведена серия из n опытов при одинаковых условиях, в каждом из которых могло появиться или не появиться событие А. Допустим, что событие А появилось в m опытах.

Число опытов, в которых появилось событие А, называется

абсолютной частотой (или просто частотой) события А. Отношение числа опытов, в которых появилось событие А к общему числу опытов в серии называют относительной частотой события А, то есть

	P* ( A) =	m	(1.1)
		n

Вероятностью случайного события А называется постоянное число,

около которого группируются относительные частоты этого события по мере увеличения числа опытов (испытаний).

Вероятность события А обозначается Р(А) или просто Р. Статистическое определение вероятности опирается на реальный эксперимент. Это и преимущество и в то же время недостаток, так как на практике чаще всего нет условий, для проведения достаточно большого числа опытов, позволяющих определить вероятность с хорошей степенью точности.

Классическое определение вероятности

Классический способ определения вероятности основан на понятии равновозможных событий, которые являются исходом данного опыта и образуют полную группу несовместимых событий. Равновозможные и несовместимые события, составляющие полную группу, называют

Рисунок 1.1

d

7

(элементарными) исходами. По отношению к каждому событию исходы делятся на благоприятные, при которых это событие происходит, и неблагоприятные, при которых событие не происходит. Обозначим число исходов, благоприятствующих событию А, через т и общее число равновозможных исходов через п.

Вероятностью события А называется отношение числа исходов, благоприятствующих появлению этого события, к общему числу всех равновозможных исходов, то есть

	P(A)=	m	(1.2)
		n

Важным достоинством классического определения является то, что с его помощью вероятность события можно определить до опыта и заранее сделать выводы. Однако этот способ имеет тот существенный недостаток, что применяется к равновозможным исходам опыта.

Вероятность события удовлетворяет двойному неравенству 0≤Р(А)≤1.

Геометрическое определение вероятности

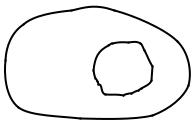
На практике часто встречаются случаи, когда число возможных исходов испытаний бесконечно. В таких случаях классическое определение вероятности неприменимо и задачу сводят к задаче о случайном выборе точки на конечном участке прямой, плоскости или пространства. При этом используют понятие геометрической вероятности. Введем понятие геометрической вероятности для двумерного случая. Пусть на плоскости имеется некоторая область D (рисунок 1.1), площадь которой SD и в ней содержится другая область d площадью Sd.

В область D наудачу бросается точка. Предположим, что вероятность события А – попадания брошенной точки в область d –

D пропорциональна площади этой области и не зависит ни от ее расположения относительно D, ни от формы d и что попадание бросаемой точки в любую точку области D равновозможно. Тогда вероятность события А – попадания точки в область d – называется

отношение площади этой области к площади всей области D, в которой может появляться данная точка, то есть

	P(А)=	Sd	(1.3)
		SD

Это определение можно распространить на одномерный и трехмерный случай.

1.2 ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Количественной характеристикой случайного результата опыта является случайная величина.

8

Случайной величиной называется величина, которая в результате испытания может принимать то или иное значение, причем заранее, до опыта, неизвестно, какое именно.

Случайные величины могут быть дискретными или непрерывными. Дискретной называют случайную величину, принимающую

отдельные, изолированные значения.

Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала.

Число возможных значений непрерывной случайной величины бесконечно.

1.3 ЗАКОН РАСПРЕДЕЛЕНИЯ. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ И ПЛОТНОСТЬ ВЕРОЯТНОСТИ, ИХ ВЗАИМОСВЯЗЬ И СВОЙСТВА

Законом распределения случайной величины X называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Для дискретной случайной величины закон распределения может быть задан в виде таблицы, графически и аналитически.

Пусть случайная величина Х принимает значения х1, х2,…, хn с

вероятностями р1, р2, …,рn, где Р(Х = хi) = pi , i = 1,n . Так как события Х = хi

(i=1,n ) образуют полную группу несовместных событий, то

n	n
∑P(X = xi )= ∑ pi =1.		(1.4)
i =1	i =1

Простейшей формой задания закона распределения дискретной случайной величины Х является таблица, в которой перечислены в порядке возрастания все возможные значения случайной величины и соответствующие их вероятности.

	хi	х1	х2		…	хn
Аналитической	pi	р1	p2		…	рn
		формой	задания		закона распределения как для

дискретных, так и непрерывных случайных величин является функция распределения.

Функцией распределения случайной величины Х называется функция F(x), определяющая вероятность того, что случайная величина Х примет

	значение меньшее x, то есть
		F(x) = P(Х < x).			(1.5)
			Функция	F(x) также называется
	Х < x		интегральной	функцией	распределения
		x	или интегральным законом распределения.
			Геометрически	функция	распределения
	x
			интерпретируется как вероятность того,

Рисунок 1.2

9

что случайная величина Х попадет левее заданной точки х (рисунок 1.2). Свойства функции распределения вероятностей:

1)0 ≤ F(x) ≤1;

2)F(x) – неубывающая функция аргумента х;

3)P(α ≤ Χ < β)= F( β ) − F(α );

4)F( −∞) = 0, F( +∞) =1.

Пусть Х – непрерывная случайная величина, тогда ее функция распределения непрерывна и кусочно-дифференцируема и имеет непрерывную производную.

Теорема 1. Вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю, то есть P(Х = x1) = 0.

Следствие. Если Х – непрерывная случайная величина, то	(1.6)
P(x1 < Х < x2) = P(x1 ≤ Х < x2).

Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f (x) – первую производную от функции распределения F(x), то есть

f (x) = F / (x).

(1.7)

Свойства плотности распределения вероятностей непрерывной случайной величины:

1)f (x)≥ 0 ;

2)∞∫ f (x)dx =1;

−∞

3) P(α < X < β)= β∫ f (x)dx ;

α

4) F(x) = ∫x f (x)dx .

−∞

Из свойств плотности распределения вероятности следует, что вероятность попадания случайной величины Х в бесконечно малый интервал длиной ∆х , содержащий точку х0 , равна f (х0) ∆х.

1.4 ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН

Если для случайной величины определен закон распределения ее вероятностей, то такая информация о ней является исчерпывающей. Однако на практике бывает достаточным знание некоторых числовых характеристик таких величин. Приведем основные числовые характеристики случайных величин и рассмотрим их вероятностный смысл.

Математическим ожиданием дискретной случайной величины

называется число

M [X ]= mx =	n
	∑xi pi .	(1.8)
	i =1
Математическим ожиданием	непрерывной	случайной величины
называется число

10

M [X ]= ∞∫xf (x)dx .	(1.9)
−∞

Случайная величина X называется независимой от случайной величины Y, если закон распределения случайной величины X не зависит от того, какое значение приняла величина Y.

Свойства математического ожидания:

1)М[С] = С, где С = const;

2)М[С Х] = С М[Х];

3)М[Х + Y] = М[Х] + М[Y];

4)М[Х Y] = М[Х] М[Y], если Х, Y – независимые случайные величины.

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, то есть

D[X] = Dx = M[(X–M[X])2].	(1.10)
Дисперсией дискретной случайной величины называется число
n
D[X ]= ∑(xi − mx )2 pi .	(1.11)
i =1
Дисперсией непрерывной случайной величины называется число
∞
D[X ]= ∫( x − mx )2 f ( x )dx .	(1.12)
−∞

Теорема 2. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания, то есть

D[X]=M[X2]– (M[X])2.

(1.13)

Свойства дисперсии:

1)D[С] = 0, где С = const;

2)D[С Х] = С2 D[Х];

3)D[Х ± Y] = D[Х] + D[Y], если Х, Y – независимые случайные величины.

Средним квадратическим отклонением случайной величины

называется число
σ[X]=σx= D[X ].	(1.14)

Асимметрией (коэффициентом асимметрии) называется число