part2

Какая из компаний чаще отказывает в посадке пассажиру, заказавше-

му билет, в связи с отсутствием мест в самолете?

7.8. Доказать, что дисперсия числа появлений успеха при однократ-

ном проведении опыта не может быть больше 0,25.

7.9. Найти математическое ожидание и дисперсию числа очков, вы-

падающих при однократном бросании игральной кости.

7.10. Монета бросается дважды. Найти закон распределения количе-

ства выпавших "орлов". Определить Mξ, Dξ и .

7.11.Найти закон распределения количества выпавших "решек" при трехкратном бросании монеты. Определить Mξ, Dξ и .

7.12.Случайная величина имеет плотность вероятности f (x) и

функцию распределения F(x). Как изменятся графики этих функций,

если

а) к случайной величине прибавить 1;

б) от случайной величины отнять 2;

в) умножить случайную величину на 2;

г) изменить знак случайный величины на противоположный?

7.13. Какими свойствами обязательно обладает функция распределе-

ния любой случайной величины:
а) четность;	б) нечетность;
в) ограниченность;	г) непрерывность справа (слева);
д) строгая монотонность;	е) нестрогая монотонность;
ж) положительность;	з) неотрицательность?

75

7.14. Какими свойствами может обладать плотность распределения

случайной величины:
а) четность;	б) нечетность;
в) ограниченность;	г) неограниченность;
д) непрерывность;	е) наличие одной точки разрыва;
ж) монотонность;	з) периодичность;
и) положительность;	к) неотрицательность?

7.15. Может ли функция

0, x 0,2

φ( x) x, x 0,1

x 1, x 1,2

быть плотностью вероятности случайной величины? Функцией рас-

пределения?

7.16. Может ли функция
0,	x ,0 1,2
	x 0,1
φ( x) x,
1,	x 2,

быть плотностью вероятности случайной величины? Функцией рас-

пределения?

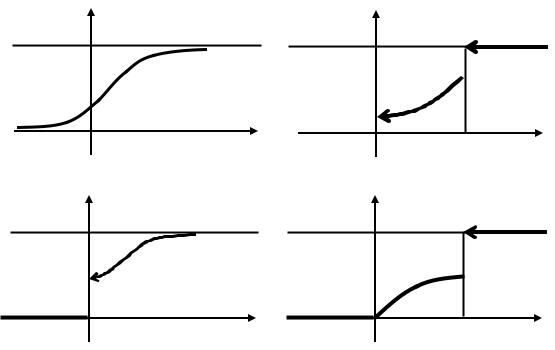
7.17. Количество нефти в резервуаре представляет собой случайную величину. Может ли ее функция распределения иметь какой-либо из графиков, изображенных на рис.15? Какова особенность наполнения резервуара нефтью в каждом из возможных случаев?

76

а)	F (x)	б)	F (x)
	1		1

0	x		0	x
в)	F (x)	г)		F (x)
1		1

0

x

0

x

Рис. 15. К задаче 7.18

7.18.Может ли второй начальный момент v2 случайной величины быть больше её дисперсии?

7.19.Случайная величина имеет плотность

2x, x 0,1 f ( x)

0, x 0,1

а) Не проводя вычислений, определить знак центрального момента третьего порядка 3. б) Найти медиану Me.

7.20. Случайная величина задана функцией распределения F(x). Вы-

яснить, является ли случайная величина непрерывной. Найти ее плотность вероятности f (x), если она существует. Построить графики

F(x) и f (x).

77

	x	,	x 0
e
а) F(x) =			x 0
1,
0,5ex , x 0
			0 x 2
в) F(x) = 0,8,
1,			x 2
0,			x 1
			1 x 2
д) F(x) = ln x,
1,			x 2

0,				x 1
			1, 1 x 2
б) F(x) = x
1,				x 2
0,					x / 2
г) F(x) = 1 sin x, / 2 x 0
1,					x 0
				0,			x 0
				sin 2x
x							0 x
е)F(x) =						,
				2
							x
				1,

7.21. Случайная величина имеет плотность вероятности (закон Ре-

лея):

0,	x 0
f (x) =	2
2axe ax	, x 0

Найти функцию распределения F(x). Построить графики F(x) и f (x)

при a = 0,5.

7.22. Случайная величина имеет плотность вероятности (закон Лап-

ласа):

f (x) = ae |x|, const 0 .

Найти коэффициент a и функцию распределения F(x). Построить графики F(x) и f (x).

7.23. Случайная величина имеет плотность вероятности

78

0,	x 0
	0 x 1
x,
f (x) =
2 x, 1 x 2
	x 2
0,

Найти: а) функцию распределения случайной величины ; б) веро-

ятность события A = {0,2 < < 0,9}; в) медиану Me.

7.24. Пусть плотность вероятности случайной величины задается формулой

0,				x 1
f (x) =	1		,	x 1
		2
x
Найти вероятности P{A1 A2} и				P{A1 + A2}, если событие A1 =

= {0 < < 2}, а событие A2 = {4 < < 5}.

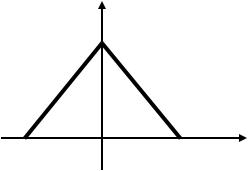
7.25. Случайная величина распределена по закону Симпсона (рис.

16). Написать выражение для плотности вероятности. Найти функ-

цию распределения и построить ее график. Определить вероятность

P{ – a/2 < < a}.

f (x) a

a		a		x

Рис. 16. Закон Симпсона

7.26. Точка брошена в круг радиуса R. Вероятность ее попадания в любую область внутри круга пропорциональна площади этой облас-

79

ти. Найти функцию распределения и плотность вероятности случай-

ной величины , равной расстоянию от точки до центра круга.

7.27. Автобусы движутся по маршруту с интервалом 10 мин. Время ожидания T автобуса на остановке имеет равномерное распределение.

Найти: а) функцию распределения и плотность вероятности; б) сред-

нее время ожидания автобуса и среднее квадратическое отклонение этого времени; в) вероятность того, что время ожидания автобуса не превысит 4 минут.

7.28. Правитель острова Хазерталь, решив ограничить численность женского населения в своем государстве, издал декрет, состоящий из двух пунктов:

1)каждой семье разрешается обзавестись не более чем одной дочерью. После рождения девочки дальнейшее увеличение семьи не разрешается;

2)общее количество детей в семье не может превышать четы-

рех.

Приняв вероятность рождения мальчика равной 0,5, выяснить,

какую часть населения острова по прошествии длительного времени будут составлять мужчины.

7.29. Решить предыдущую задачу после отмены правителем второго пункта указа.

80

8. Специальные виды распределений

екоторые частные виды распределения дискретных и непре-

Нрывных случайных величин особенно часто встречаются в при-

кладных задачах теории вероятностей. Для вычисления их основных числовых характеристик удобно пользоваться готовыми формулами.

Рассмотрим основные виды дискретных распределений.

Биномиальное распределение

Случайная величина ξ имеет биномиальное распределение с па-

раметрами (n, p), (0 < p < 1, n ≥ 1), если она принимает значение ξ = k

с вероятностью

P k Cnk pk 1 p n k , k = 0, …, n.

Математическое ожидание и дисперсия биномиально распреде-

ленной случайной величины ξ определяются выражениями: Mξ = np;

Dξ = npq, где q = 1 – p.

Геометрическое распределение

Случайная величина ξ имеет геометрическое распределение с

параметром р, (0 < p < 1), если она принимает значение ξ = k с веро-

ятностью

P{ξ = k} = p(1– p)k; k = 0, 1, 2, … .

Геометрически распределенная случайная величина имеет харак-

теристики:	M	1 p	; D	1 p	.
		p		p2

81

Распределение Пуассона

Случайная величина ξ имеет распределение Пуассона с пара-

	метром a, (где a > 0), если
	P k	ak	e a ,	k = 0, 1, 2, ….
		k !
	Для распределения Пуассона Mξ = a;			Dξ = a.

Опишем теперь важнейшие непрерывные распределения слу-

чайных величин.

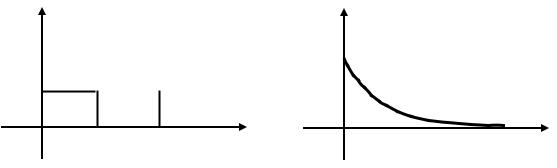
Равномерное распределение

Случайная величина ξ имеет на интервале [a; b] равномерное распределение, если ее плотность вероятности постоянна на этом ин-

тервале (рис. 17), т.е.

1

, x a;b

a

f ( x) b

x a;b .

0,

f (x)

f (x)

a

a

1

b a

0

a

b

x

0

x

Рис. 17. Равномерное

Рис. 18. Показательное

распределение

распределение

Математическое ожидание равномерно распределенной случай-

ной величины ξ есть M

a b

, дисперсия D b a 2 .

2

12

82

Показательное (экспоненциальное) распределение

Случайная величина ξ имеет показательное распределение с

параметром λ, (λ > 0), если ее плотность вероятности (рис. 18) опре-

деляется зависимостью

							x	, x 0
						e
				f ( x)
						0,		x 0.
Показательно распределенная случайная величина ξ имеет ха-
рактеристики:	M	1	;	D	1	.
					2

Нормальное распределение

Случайная величина ξ имеет нормальное (гауссовское) распре-

деление с параметрами (a; 2), если ее плотность вероятности опре-

деляется выражением:

( x a)2

f ( x) 1 e 2 2 , x ; . 2

Функция распределения нормально распределенной случайной величины представляется интегралом, не выражаемым через элемен-

тарные функции:

				x		(t a)2
		1
						2 2
F ( x)				e			dt .
		2

Параметр a нормального распределения имеет смысл математи-

ческого ожидания случайной величины ξ: Mξ = a; параметр 2 пред-

ставляет ее дисперсию: Dξ = 2. Медиана нормального распределения

83

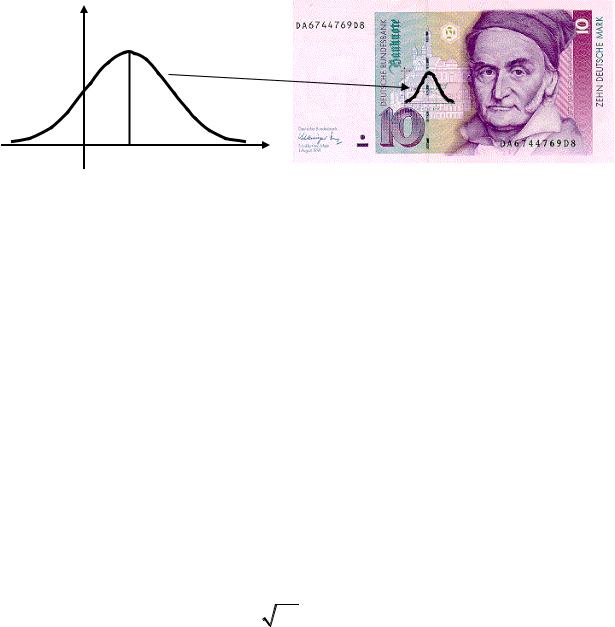
совпадает с математическим ожиданием: Me = Mξ = a; асимметрия равна нулю: A = 0.

График функции f (x) носит название гауссовой кривой (рис.19).

Там же справа представлена банкнота в 10 марок ФРГ, которая ис-

пользовалась до введения евро. На банкноте была изображена гауссо-

ва кривая и ее первооткрыватель – великий немецкий математик Карл Фридрих Гаусс (1777 – 1855).

f (x)

0 a x

Рис. 19. Нормальное (гауссовское) распределение

Для краткости нормальное распределение с параметрами (a; 2)

обозначают N(a; 2). Если случайную величину ξ нормировать, т.е.

вычесть из нее постоянную величину a и разделить на , то получен-

ная случайная величина a будет иметь распределение N(0;1) –

так называемое, стандартное нормальное распределение.

Функция распределения стандартного нормального распределе-

ния табулирована и обозначается через Fo(x):

Fo (x)		1				x	e t	2	/2dt .
		2
			84