part2

Эта функция обладает свойством:		Fo(– x) = 1 – Fo(x).
Вероятность попадания нормально распределенной случайной
величины N a, 2 в заданный интервал (c, d )							находится по фор-
муле
P c d F	d a			F	c a			.
o				o

Эта вероятность может быть выражена через табулированную функцию Лапласа (см. Приложение)

	1			x		t2
( x)						2 dt
				e
		2
			0

аналогичным образом:

	d a			c a
	P c d

Функция Лапласа (x) изображена на рис. 20.

(x)

N (0,1)

0,5

(x)

0

x

0	x	x	– 0,5

Рис.20. Функция Лапласа

Отметим важные свойства функции Лапласа:

1.( – x) = – (x), т.е. (x) – нечетная функция.

2.(x) – монотонно возрастающая функция.

85

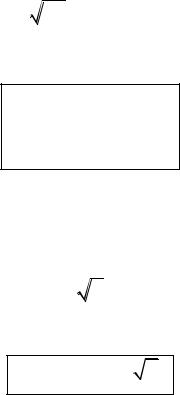
3. lim (x) 0,5;	lim ( x) 0,5.
x	x

Полезно запомнить следующие важные значения функции Лапласа:

(2) = 0,9545 / 2 = 0,47725;			(3) = 0,9973 / 2 = 0,49865.
Вероятность попадания нормально распределенной случайной
величины N (a, 2 ) в интервал,			симметричный относительно ма-
тематического ожидания a, может быть вычислена по формуле
P{	a	} 2			.

Правило 3 . Для нормально распределенной случайной вели-

чины попадание в интервал [a – 3 ; a + 3 ] представляет собой прак-

тически достоверное событие. Его вероятность близка к единице:

P{a 3 a 3 } 2 (3) 0,9973.

Замечание.	В литературе					встречаются и иное определение
	( x)	1			x	e t2 /2dt . Функции	(x), F (x) и
функции Лапласа:
	1						o
			2 x

1(x) легко выражаются одна через другую:

Fo(x) = (x) + 0,51(x) = 2 (x)

Помимо перечисленных выше функций, иногда используют так называемую функцию ошибок:

erf ( x)	2			x	t2 dt ,
				e
			0

которую также легко связать с функцией Лапласа:

erf ( x) 2 ( x 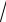2)

86

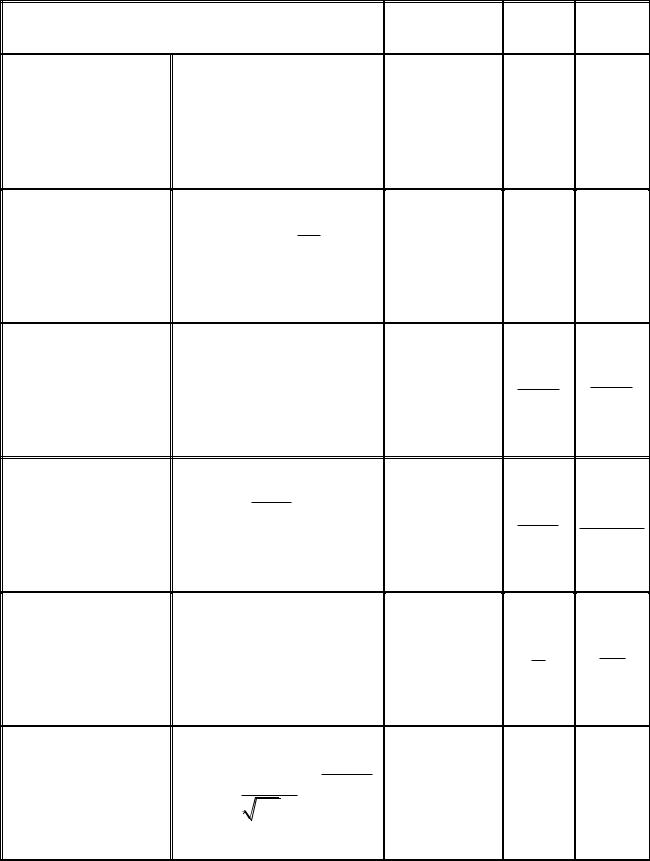
Основные виды распределения случайных величин

Распределение

Параметры

Mξ

Dξ

P k

Ck pk 1 p n k

n, p

n

n p

n pq

Биномиальное

k = 0, 1, 2, …, n

(n N ,

0 < p < 1)

Пуассона

P k ak e a

a

a

a

k !

(a > 0)

k = 0, 1, 2, …

Геометрическое

P{ξ = k} = p(1– p)k

p

1 p

1 p

(0 < p < 1)

p2

k = 0, 1, 2, …

p

1

, x a; b

Равномерное

f ( x)

a, b

a b

(b a)

2

b

a

a; b

(a < b)

2

12

0,

x

x

,

x 0

f ( x)

e

1

1

Показательное

0,

x 0

( > 0)

2

Нормальное

( x a)2

a,

1

(гауссовское)

2

2

(a ,

2

f ( x)

2 e

a

2

> 0 )

N(a, )

87

ПРИМЕР 1. Контрольное задание (тест) состоит из 10 вопросов,

предусматривающих ответы «да» и «нет». Тестируемый решил на каждый вопрос давать ответ наудачу. Найти: а) среднее число пра-

вильных ответов; б) вероятность того, что он ответит правильно на все вопросы; в) вероятность того, что он ошибется не более двух раз.

Решение. В данном примере проводится 10 испытаний Бернул-

ли с вероятностью успеха в каждом p = 1/2. Следовательно, случай-

ная величина ξ – количество правильных ответов – подчиняется би-

номиальному закону распределения с параметрами n = 10; p = 1/2.

Тогда	имеем:				а) M np 10						1	5 ;	б)
										2
P	10 C	10			1		10		1	; в) вероятность ошибиться не более двух
	10				2				210

раз, т.е. два раза или меньше, равна вероятности P{ξ 8} дать 8 или более правильных ответов, и может быть найдена двумя способами:

			k			1		k				10 k				k			10
P 8	10										1			10					1
		C													C						,
		10													10
	k 8					2					2			k 8					2

либо через вероятность противоположного события

			k			10
P 8 1 P 8 1	7					1
		C						.
		10
	k 0					2

(Первый способ, разумеется, предпочтительней, т.к. требует нахож-

дения суммы лишь трех слагаемых при k = 8, k = 9 и k = 10).

ПРИМЕР 2. Случайная величина ξ – напряжение в электриче-

ской сети – изменяется по нормальному закону с параметрами a =

88

f ( x) k e

= 220 В и = 3 В. Определить вероятность того, что случайная вели-

чина ξ отклонится от математического ожидания не более, чем на 5 В.

Решение. Случайная величина ξ N (220; 32). Отклонение

случайной величины ξ от математического ожидания возможно в обе

стороны, поэтому нужно вычислить вероятность

				5			2 1, 67 0, 905 , где значение
P{	a		5} 2					(1,67) = 0,4525
				3

найдено по таблице функции Лапласа.

Задачи к разделу 8

8.1. Случайная величина ξ равномерно распределена на отрезке

[1; 13]. Написать выражение для её плотности вероятности и функции распределения и изобразить их графически. Вычислить, не пользуясь готовыми формулами, величины Mξ , Dξ и . Найти вероятность по-

падания случайной величины ξ в отрезок [4; 27].

8.2. Плотность вероятности нормально распределенной случайной величины имеет вид

( x 2)2

18 .

Найти коэффициент k и параметр . Написать вид функции распреде-

ления F(x). Найти: F(–1,3); F(4,1); вероятность попадания случайной величины в промежуток [2; 5].

8.3. Случайная величина распределена по нормальному закону с па-

раметрами a и . Написать выражение для плотности вероятности и

89

функции распределения и изобразить их графически. Пользуясь пра-

вилом "трех сигм", найти интервал, в который практически достовер-

но (с вероятностью 0,997) попадает случайная величина :

а) a = 0 , = 1 ;	б) a = 2 , = 1 ;
в) a = – 2 , = 1 ;	г) a = 0 , = 0 , 5 .
8.4. Случайная величина	распределена по нормальному закону

N (1, 2) . Какое событие более вероятно: 3 4 или –1 0 ?

8.5. Давление на выходе компрессорной станции представляет собой случайную величину, имеющую нормальный закон распределения с параметрами a = 5 106 Па и = 2 105 Па. Найти вероятности собы-

тий:

A давление в системе превысит 5,4 106 Па,

Bдавление в системе не превзойдет 4,7 106 Па,

Cдавление в системе будет в пределах (4,9 5,2) 106 Па.

8.6. Суточный дебит скважины на газовом промысле можно считать случайной величиной , имеющей нормальный закон распределения с математическим ожиданием a = 1 106 м3 /сут и средним квадрати-

ческим отклонением = 0,2 106 м3 /сут. Найти вероятности событий:

A суточный дебит будет больше 1,5 106 м3 /сут,
B суточный дебит не превысит 0,9 106 м3 /сут,
C суточный дебит заключен в пределах	(0,8 1,2) 106 м3 /сут.
8.7. Имеются два прибора, относительные ошибки 1		и 2 измерения
которых распределены по нормальному	закону:	1 N (0; 0,16) ,
90

2 N (0,1; 0, 09) . Каким прибором следует воспользоваться, чтобы вероятность относительной ошибки, превышающей 50%, была наи-

меньшей?

8.8. Участок газопровода между двумя компрессорными станциями

(КС) имеет длину 100 км. Появление утечки газа равновероятно в любой точке участка. Какова вероятность, что она произойдет ближе

10 км от одной из КС?

8.9. В условиях предыдущей задачи в середине газопровода имеется участок длиной 20 км, где из-за характера местности плотность веро-

ятности утечки в два раза выше, чем в остальной части газопровода.

Написать выражение для плотности вероятности и функции распре-

деления расстояния до места утечки газа. Найти математическое ожидание и дисперсию этой случайной величины. Найти вероят-

ность, что утечка произойдет ближе 10 км от одной из КС.

8.10.Случайные величины 1 и 2 распределены по биномиальному закону с параметрами n1= 20, p1= 0,2 и n2= 20, p2= 0,3. Какое событие более вероятно: 1 8 или 2 8?

8.11.Случайные величины и распределены по экспоненциально-

му закону с параметрами 2 и 4 соответственно. Какое событие более вероятно: 0 3 или 0 3 ?

8.12.	Случайная величина распределена по экспоненциальному за-
кону	с параметром = 2. Найти условную вероятность

P { ( < 2 a ) / ( > a ) }, если a = 0,5.

91

8.13. Количество заявок от геологических партий на использование специальной аппаратуры представляет собой случайную величину,

распределенную по закону Пуассона. В среднем за месяц поступает

24 заявки. Найти вероятность событий:

А – за месяц будет более 24 заявок;

B – в течение 5 суток аппаратура будет простаивать;

C – на протяжении 10 суток поступит не менее 7 заявок.

8.14. Число отказов за год на участке магистрального трубопровода подчинено закону Пуассона с параметром a = 0,8 (1/год). Найти: а)

среднее время безотказной работы участка; б) через какой промежу-

ток времени вероятность появления отказа превысит 0,5? в) вероят-

ность того, что в течение трех лет будет не менее двух отказов.

8.15. Эксплуатируются 5 скважин, каждая из которых за месяц может,

независимо от других, выйти из строя с вероятностью 0,1. Необходи-

мая подача нефти обеспечивается, если исправны, по крайней мере, 3

скважины. Какова вероятность обеспечения необходимой подачи нефти?

8.16. Среди 12 одинаковых конденсаторов есть 2 перегоревших. Кон-

денсаторы по очереди вставляются в цепь, пока не будут выявлены оба перегоревших. Какова вероятность, что понадобится ровно 7 ис-

пытаний?

8.17. Бросается монета до первого появления "решки". Случайная ве-

личина равна количеству бросаний. Найти закон распределения случайной величины и вероятность события { < 3 }.

92

8.18. Бросается игральная кость до первого появления шестерки.

Случайная величина равна количеству бросаний. Найти закон рас-

пределения случайной величины и вероятность события { < 6 }.

8.19. На пути движения автомобиля 6 светофоров, на каждом из кото-

рых горит с вероятностью 0,5 зеленый свет, и с такой же вероятно-

стью – красный. Найти закон распределения случайной величины –

числа светофоров, пройденных автомобилем до первой остановки.

8.20.Какова максимально возможная вероятность достижения двух успехов в серии из 3 испытаний Бернулли?

8.21.(Гамма – распределение). Время безотказной работы конденса-

торов хорошо описывается случайной величиной с плотностью ве-

роятности

	0,		x 0,
f ( x) p
		x p 1e x , x 0,
	( p)

где ( p) 0 x p 1e xdx – гамма-функция, для натуральных значений p удовлетворяющая равенству ( p) ( p 1)!. (Для натуральных p

гамма-распределение носит название распределения Эрланга).

а) Доказать, что при p=1 гамма-распределение совпадает с экс-

поненциальным;

б) найти функцию распределения случайной величины ;

в) для значений параметров p = 3, = 0,5 1/год определить веро-

ятность безотказной работы конденсатора в течение 3 лет;

93

г) доказать, что M = p , D = p2 .

8.22. (Логарифмически нормальное распределение). Плотность ве-

роятности случайной величины задана функцией

		0,						x 0,
							(ln x a)2
f ( x)		1
							2 2
					e			, x 0.
x			2

а) Построить график плотности вероятности логарифмически нор-

мального распределения.

б) Найти функцию распределения случайной величины и построить ее график.

в) Найти математическое ожидание и дисперсию случайной величи-

ны .

г) Найти вероятности событий: A = {0 < < 2}, B = {1 < }.

94