part2

9.Системы случайных величин

Совокупность двух и более случайных величин называется сис-

темой случайных величин, или случайным вектором. Функ-

ция распределения пары случайных величин ξ, η (координат случай-

ного вектора) определяется формулой

F(x, y) P{ x, y}.

Для системы n случайных величин ξ1, …, ξn функция распреде-

ления определяется формулой

F(x1, x2...xn ) P{ 1 x1, 2 x2, ..., n xn}.

Функция распределения пары случайных величин обладает сле-

дующими свойствами:

1)F(x, y) не убывает по каждому из своих аргументов.

2)F( , ) F( , y) F(x, ) 0.

3)F( , ) 1.

4)F(x, ) F (x), F( , y) F ( y), где Fξ(x) и Fη(y) – функ-

ции распределения величин и η, соответственно.

Закон распределения пары случайных величин дискретного типа может быть задан матрицей

ξ	η	y1	y2	…	yn
	x1	p11	p12	…	p1n
	x2	p21	p22	…	p2n
	…	…	…	…	…
	xm	pm1	pm2	…	pmn
			95

где x1, x2, …, xm – возможные значения величины ξ; y1, y2, …, yn –

возможные значения величины η. В ячейках таблицы расположены вероятности событий

pij P{ xi , y j}.

Вероятности pij удовлетворяют условиям:

1 ) pij 0 ,

	m n
2)	pij 1,
	i 1 j 1
	m
3)	p{ y j} p j pij ,
	i 1
	n
4)	p{ xi} pi pij .
	j 1

Если величины ξ, η – непрерывного типа, то закон их совместно-

го распределения может быть задан плотностью распределения веро-

ятностей:

f (x, y) lim	P{x x x, y y y}	.
x 0	x y
y 0

Плотность и функция распределения двумерной случайной вели-

чины связаны соотношениями:

f (x, y)	2F (x, y)	, F (x, y)	x	y
	x y			f (x, y)dxdy.

Плотность вероятности f (x, y) пары случайных величин обладает

свойствами:

96

1)	f (x, y) 0.
			f (x, y)dxdy 1.
2)
3)	f (x) f (x, y)dy,			f ( y) f ( x, y)dx,

где f (x), f ( y) – плотности случайных величин ξ и η.

Вероятность попадания случайной точки в некоторую область D

выражается через плотность вероятности f (x, y) :

P{( , ) D} f ( x, y)dxdy.

D

Условные плотности распределения, т.е. плотности вероятно-

сти одной из случайных величин при условии, что другая принимает фиксированное постоянное значение, определяется формулами:

f (x / y)	f (x, y)	,	f ( y / x)	f ( x, y)	.
	f ( y)			f (x)

Случайные величины ξ, η называются независимыми, если их функция распределения равна произведению функций распределения компонент ξ и η:

F(x, y) = Fξ (x) Fη(y).

Для непрерывных независимых случайных величин ξ, η услов-

ные и безусловные плотности вероятностей совпадают: f (x/y) = fξ (x)

и f (y / x) = fη(y), а двумерная плотность равна произведению плотно-

стей компонент:

f (x, y) = fξ (x) fη(y).

97

Начальные моменты пары случайных величин ξ, η определяют-

ся формулами (k, s – целые, k, s 0 ):

			xik			ysj pij					(для дискретных величин)
					j
	vks		i
					x	k	y	s	f (x, y) dx dy		(для непрерывных величин)
При этом v10 M ,							v01 M .
Аналогично определяются центральные моменты пары слу-
чайных величин ξ и η:
( xi M )k ( y j M )s pij											(для дискретных величин)
		j
i
ks
			( x M )k ( y M )s f ( x, y)dxdy (для непрерывных величин)
При этом				2 D ,						2	D .
		20							02

Второй смешанный центральный момент μ11 называется корреля-

ционным моментом, (или ковариацией) случайных величин ξ и η:

K cov( , ) 11 M ( M )( M ) M M M .

Вместо корреляционного момента часто используют безразмерную величину

r K ,

называемую коэффициентом корреляции.

Замечание. Если две случайные величины независимы, то их коэффициент корреляции равен нулю. Обратное утверждение, вооб-

98

ще говоря, неверно: если две случайные величины некоррелированы,

т.е. их коэффициент корреляции равен нулю, то они вовсе не обяза-

тельно являются независимыми.

Пусть ξ, η – произвольные случайные величины, μ11 – их корре-

ляционный момент, С – постоянная (не случайная) величина. Тогда математическое ожидание и дисперсия обладают следующими свой-

ствами:

1)М(С) = С;

2)М(Сξ) = C Mξ;

3)M(ξ + η) = Mξ + Mη;

4)M(ξ η) = Mξ Mη + μ11;

5)D 0;

6)D(С) = 0;

7)D(Сξ) = C2 Dξ;

8)D(ξ η) = Dξ + Dη 2μ11.

Вчастном случае некоррелированных случайных величин ξ и η

равенства 4) и 8) упрощаются и принимают вид:

M (ξη) Mξ Mη,

D(ξ η) Dξ Dη .

Коэффициент корреляции r случайных величин ξ, η удовлетворя-

ет неравенству

– 1 r 1

Абсолютная величина коэффициента корреляции равна 1 в том и только в том случае, если ξ и η связаны линейной функциональной зависимостью

99

a b,

где a и b – детерминированные величины, причем r = +1 при a > 0 и r = – 1 при a < 0. Коэффициент корреляции характеризует меру ли-

нейной зависимости между случайными величинами.

Основными числовыми характеристиками системы n случай-

ных величин ξ1, …, ξn служат математические ожидания Mξi, дис-

персии Dξi= i2 и корреляционные моменты каждой пары величин

(ξi, ξj):

kij = M[(ξi – Mξi) (ξj – Mξj)], (i, j 1, ,n ).

Матрица, составленная из корреляционных моментов, называет-

ся корреляционной (ковариационной) матрицей:

k11	k12	...		k1n
K k21	k22	...	k2n .
...	...	...	...
	kn2
kn1		...		knn
Коэффициенты корреляции	rij	kij		образуют нормированную
		i j
корреляционную матрицу:
1	r12	...	r1n
r	1	...	r
R 21				2n	.
...	...	...		...
	rn2
rn1		...	rnn

100

Корреляционная матрица K и нормированная корреляционная матрица R симметричны относительно своих главных диагоналей.

Двумерное нормальное распределение

Система двух случайных величин непрерывного типа с плотно-

стью вероятности

f ( x, y)	1				e G( x, y) ,
	2	1 r2

где

		1		( x a )2		2r( x a )( y a )				( y a )2
G( x, y)												,
				2						2
2(1		r2 )

называется распределенной по нормальному закону. Нормальное распределение на плоскости зависит от 5 параметров aξ, aη, σξ, ση, r,

причем величины aξ и aη являются математическими ожиданиями случайных величин ξ и η, соответственно, σξ2 и ση2 – их дисперсия-

ми, а r – коэффициентом корреляции.

ПРИМЕР 1. Закон распределения системы случайных величин

(ξ, η) задан таблицей

yi	0	1	2	3
xi
–1	0,02	0,06	0,08	0,04
0	0,03	0,12	0,2	0,15
1	0,05	0,02	0,22	0,01
		101

Найти: а) закон распределения случайной величины η; б) Mη и

Dη; в) условный закон распределения величины η при условии, что ξ приняла значение равное 0; г) являются ли величины ξ и η независи-

мыми?

Решение.

а) Найдем вероятности событий

P 0 P 0; 1 P 0; 0 P 0; 1

0, 02 0, 03 0, 05 0,1.

P 1 P 1; 1 P 1; 0 P 1; 1

0, 06 0,12 0, 02 0, 2.

P 2 P 2; 1 P 2; 0 P 2; 1

0, 08 0, 20 0, 22 0,5.

P 3 P 3; 1 P 3; 0 P 3; 1

0, 04 0,15 0, 01 0, 2.

Теперь может быть записан закон распределения случайной величи-

ны η:

yj	0	1	2	3
pj	0,1	0,2	0,5	0,2

(Легко проверить, что p j 1).

j

б) Математическое ожидание случайной величины η:

M y j p j 0 0,1 1 0, 2 2 0,5 3 0, 2 1,8. j

Дисперсия случайной величины η:

D y2 p	j	M 2	0 0,1 1 0,2 4 0,5 9 0,2 1,82 0,76.
j
j
			102

P xi

в) Условные вероятности находятся из теоремы умножения по формуле Байеса:

P ( y j ) / ( xi ) P y j , xi .

Поскольку P 0 0, 03 0,12 0, 20 0,15 0,5 , получаем

P ( 0) / ( 0)	0, 03			0.06 ;	P ( 1) / ( 0)	0,12			0, 24 ;
0,5					0,5
P ( 2) / ( 0)		0, 20		0, 4 ;	P ( 3) / ( 0)		0,15		0, 3.
0,5					0,5

Таким образом, условный закон распределения η при условии, что случайная величина ξ приняла значение xi = 0, имеет вид

yj {ξ = 0}	0	1	2	3
qj	0,06	0,24	0,4	0,3

(Как и следовало ожидать, P ( j) / ( 0) 1).

j

г) Безусловный и условный (при условии, что ξ = 0) законы рас-

пределения случайной величины η не совпадают. Следовательно,

случайные величины ξ и η зависимы.

ПРИМЕР 2. Совместная плотность распределения случайных величин ξ и η задана функцией

3(x y),		( , ) D
f (x, y)	0,	( , ) D,

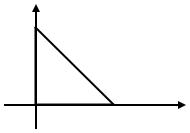
где область D заштрихована на рис.21.

Найти:

а) плотности распределения случайных величин ξ и η;

103

б) Mξ и Dξ; M и D ;

в) условную плотность случайной величины η;

г) ковариацию случайных величин ξ и η;

д) коэффициент корреляции;

е) выяснить, зависимы ли величины ξ и η.

y

1

x

0 1

Рис. 21. К примеру 2

Решение.

а) Плотности распределения случайных величин ξ и η:

			1 x			1 x																						y		2		1 x					3	(1 x2 ) ;
f		( x)		f ( x, y)dy 3						( x y)dy 3 xy
																													2			0				2
			0			0
			1 y			1 y											x2										1 y								1 y				3		y2 )
f ( y)				f ( x, y)dx 3						( x y)dx 3																				xy										(1
																							2																2
			0			0																				0										0
б) Математическое ожидание и дисперсия ξ:
				1				3		1											3
		M xf				( x)dx				x(1 x2 )dx													;
				0			2			0										8
		D M			2	(M )	2					3		1	2	(1 x	2	)dx											3			2				19		.
														x
												2		0															8							320
Математическое ожидание и дисперсия :
				1					3		1											3
		M y f ( y)dy									y(1 y2 )dy																;
				0			2				0									8
												104