Дискретные случайные величины

Будем в дальнейшем рассматривать только такие эксперименты, результаты которых имеют численное значение. Это значение будем называть случайной величиной. Случайная величина может бытьдискретной(принимать конечное или бесконечное число отдельных значений) илинепрерывной(принимать любые значения на некотором промежутке числовой оси). Разумеется, число возможных значений непрерывной случайной величины всегда бесконечно.

Например, выбор наугад любого числа из множества чисел {1; 2; 5}, или из {0; 0,5; 1; 10,5}, или из множества натуральных чисел, или любого целого числа от 5 до 10 представляет собой дискретную случайную величину.

Выбор наугад любого числа из промежутка [1; 5], или любого положительного числа представляет собой пример непрерывной случайной величины.

Закон распределения случайной величины. Математическое ожидание

Шрифт: полужирный, Отступ: Первая строка: 0 см, По центру, интервал Перед: 30 пт, После: 30 пт, Не отрывать от следующего, Уровень 2, Стиль: Связанный, Скрыть до использования, Экспресс-стиль, Основан на стиле: Обычный, Следующий стиль: Обычный

Среднее значение дискретной случайной величины, полученное при неограниченно большом числе опытов, называют ее математическим ожиданием.

Пусть проведено n экспериментов, в которых определялось значение случайной величины х. В этих экспериментах она принимала значения х₁, х₂,. . . , х_m соответственно h(x₁), h(x₂), . . ., h(x_m) число раз (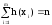). Величины h(x_i) называютчастотами.

Например, рассмотрим балл, полученный студентом на экзамене, как дискретную случайную величину. Пусть из 100 студентов в потоке один человек получил два балла, 10 человек получили три балла, 40 человек получили четыре балла и 49 человек получили пять баллов. Т.е. m= 4, х₁= 2, h(x₁) = 1; х₂= 3, h(x₂) = 10; х₃= 4, h(x₃) = 40; х₄= 5, h(x₅) = 49. Рассчитаем средний балл. Для этого просуммируем общее количество баллов, набранное всеми студентами потока, как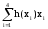= 1*2 + 10*3 + 40*4 + 49*5 = 437. Теперь разделим эту сумму на всех студентов 437/100 = 4,37. Итак, средний балл= 4,37.

Общая формула для расчета среднего значения имеет следующий вид:

При достаточно большом n число(относительную частоту) можно рассматривать, как эмпирическую оценку вероятности того, что случайная величина примет значение х_i, т.е. Р(х = х_i) =. Можно записать следующее выражение для математического ожидания случайной величины х:

М(х) = .

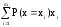Если дискретная случайная величина может принимать бесконечное число значений, сумма в правой части будет представлять собой ряд. Если этот ряд не сходится абсолютно, то говорят, что математическое ожидание данной случайной величины не существует.

Правило, позволяющее поставить в соответствие случайной величине некоторую вероятностную меру, будем называть законом распределенияслучайной величины, или еевероятностным распределением.

Для дискретной случайной величины с конечным числом значений это набор вероятностей, соответствующий каждому из ее значений.

При этом сумма этих вероятностей по всем возможным значениям случайной величины должна быть равна 1: .

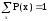Это может быть, например, таблица или формула.

Рассмотрим пример. Пусть вероятность того, что игрок выиграет 1000 руб., равна 0,1. Вероятность выигрыша 500 руб. равна 0,2. В случае проигрыша ему придется уплатить 300 руб. Представить вероятностное распределение выигрыша в виде таблицы и определить ожидаемый выигрыш.

Случайная величина х – выигрыш – может принимать значения из множества {1000; 500; -300}. Вероятность первых двух значений задана, а вероятность проигрыша можно подсчитать как 1-(0,1 + 0,2) = 0,7.

Вероятностное распределение х можно представить в виде табл.1:

Таблица 1

х	1000	500	-300
Р(х)	0,1	0,2	0,7

Отсюда математическое ожидание выигрыша М(х) = 1000*0,1 + + 500*0,2 + (-300)*0,7 = -10.

Это означает, что ожидаемый выигрыш представляет собой проигрыш. При многократном повторении эксперимента (игры) игрок потеряет в среднем 10 руб. за игру (хотя в отдельной игре он может и выиграть).

Две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какое значение приняла другая величина.

Приведем без доказательства некоторые свойства математического ожидания:

1) Математическое ожидание константы равно самой константе:

с – constM(c) =c

Например, если работник получает постоянную зарплату х = 30 (тыс. руб.), то ее математическое ожидание, т.е. ожидаемая зарплата будет равна 30 тыс.руб.

2) Постоянный сомножитель можно вынести за знак математического ожидания:

с – const 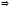M(cx) = cM(x)

Например, если один работник получает в среднем 20 тыс. руб. (х – его заработная плата, М(х) = 20), а другой работник всегда получает на 20% больше, чем первый, то заработная плата второго работника равна 1,2*х, а ее математическое ожидание равно М(1,2*х) = 1,2*М(х) = 1,2*20 =24 (тыс.руб.).

3) Математическое ожидание суммы случайных величин равно сумме математических ожиданий:

M(x + y) = M(x) + M(y)

Например, если в отделе работают два человека, и ожидаемая заработная плата одного из них равна 20 тыс. руб. (х – его заработная плата, М(х) = 20), а другого – 30 тыс. руб. (y– его заработная плата, М(y) = 30), то ожидаемая оплата труда в этом отделе равна М(х +y) = М(х) + М(y) = 20 + + 30 =50 (тыс.руб.).

4) Для независимых случайных величин математическое ожидание их произведения равно произведению математических ожиданий:

M(xy) = M(x)M(y) (для независимых х и y)

Например, пусть один работник получает в среднем 20 тыс. руб. (х – его заработная плата, М(х) = 20). Для заработной платы другого работника действует повышающий коэффициент по сравнению с первым работником, и этот коэффициент представляет собой случайную величину y. В среднем он получает на 20% больше, чем первый, т.е. М(y) = 1,2. Величина коэффициента не зависит от зарплаты первого работника. Тогда ожидаемая заработная плата второго работника равна М(хy) = M(x)M(y) = 1,2*20 =24 (тыс.руб.). Однако, если повышающий коэффициент зависит от зарплаты (например, при зарплате до 18 тыс.руб. от равен 1,21, от 18 до 20 тыс.руб. – 1,2, больше 20 тыс.руб. – 1,18), то тогда воспользоваться формулой нельзя.

Свойства (3) и (4) будут верными не только для двух, но для любого конечного числа случайных величин.

5) При увеличении (уменьшении) всех значений случайной величины на константу, ее математическое ожидание увеличится (уменьшится) на эту же константу:

с – constM(x - с) = M(x) – с

Например, если ожидаемая зарплата за месяц составляет 30 тыс. руб. (х – заработная плата, М(х) = 30), и из нее каждый месяц вычитают 800 руб. на оплату проездного билета, то математическое ожидание зарплаты за вычетом оплаты проездного составит М(х – 0,8) = М(х) – 0,8 = 29,2 (тыс.руб.).

6) Математическое ожидание отклонения случайной величины от своего математического ожидания равно нулю:

M(x – М(х)) = 0

Например, если ожидаемая зарплата за месяц составляет 30 тыс. руб. (х – заработная плата, М(х) = 30), то ее ожидаемое отклонение от 30 тыс. руб. составляет ноль.