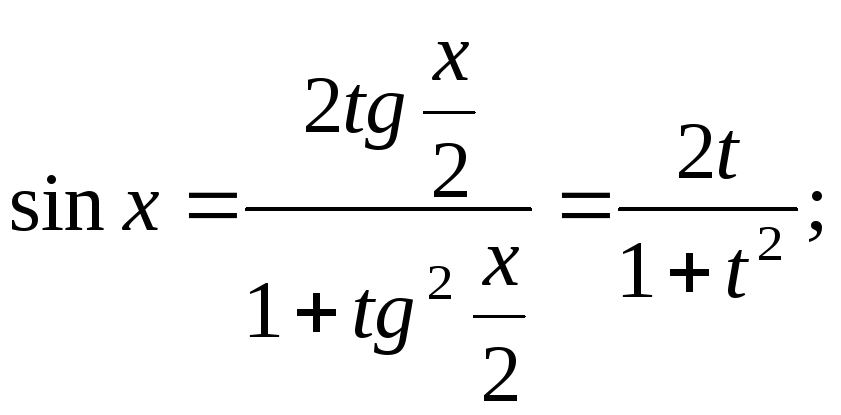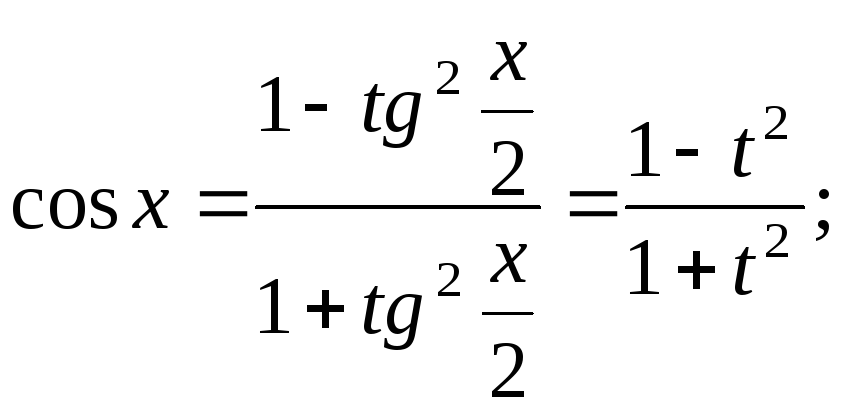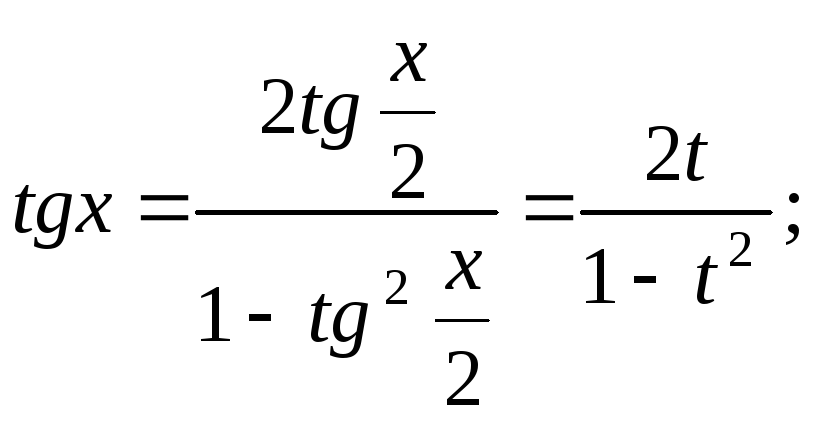См. Приложение 3 Некоторые методы интегрирования

а) метод замены или подстановки;

Функцию х=φ(t) выбирают так, чтобы интеграл был более простым, чем данный.

Часто более целесообразно использовать замену не в виде , а в виде

Пример 3. Найти .

Решение:

Пусть тогда откуда

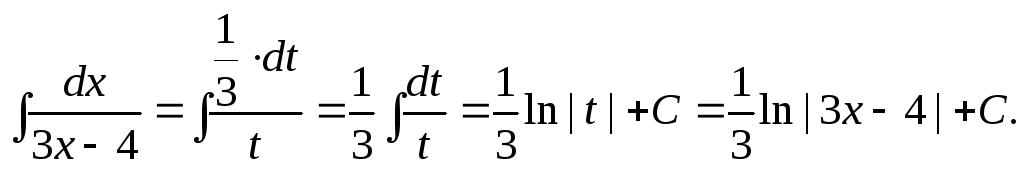
Пример 4. Найти

Решение:

Сделаем замену , тогда

б) метод «интегрирования по частям»

Если ∫f(х)dх не является табличным, то его представляют в виде

,

где u и v - некоторые дифференцируемые функции.

Формула интегрирования по частям:. (16)

Этот метод следует применить, если интеграл не более сложный, чем интеграл . Иногда этот метод в процессе решения нужно применять несколько раз.

Применение метода интегрирования по частям

Интеграл вида:	Указания для решения
- многочлен -й степени	Последовательно интегрировать частями,
	Двукратное применение интегрирования по частям
	- соответствующая обратная тригонометрическая функция

Пример 6. Найти .

Решение:

Пример 7. Найти

Решение:

Пример 6. Найти .

Решение:

Пример 7. Найти

Решение:

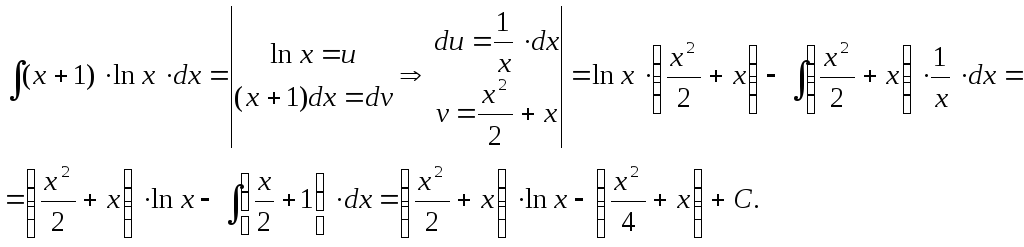
в) Интегрирование рациональных дробей

Определение Простыми или элементарными дробями называют выражения вида:

где - действительные числа, - целое положительное число больше единицы, имеет комплексные корни, то есть его дискриминант меньше нуля.

Теорема: Каждую правильную рациональную дробь можно выразить в виде конечной суммы простых дробей. При этом коэффициенты разложения определяют по методу неопределенных коэффициентов.

Каждая из четырех элементарных дробей интегрируется:

1.

2.

Поделив числитель и знаменатель дроби на получаем. Тогда: 3.

Пример 10. Вычислить интеграл

Решение:

Представим дробь в виде элементарных дробей:

Приравняем числители и приравняем коэффициенты при степенях переменной:

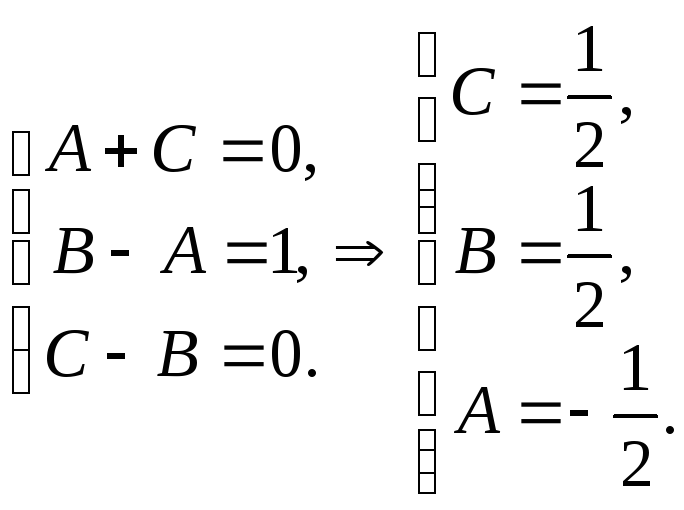
Таким образом:

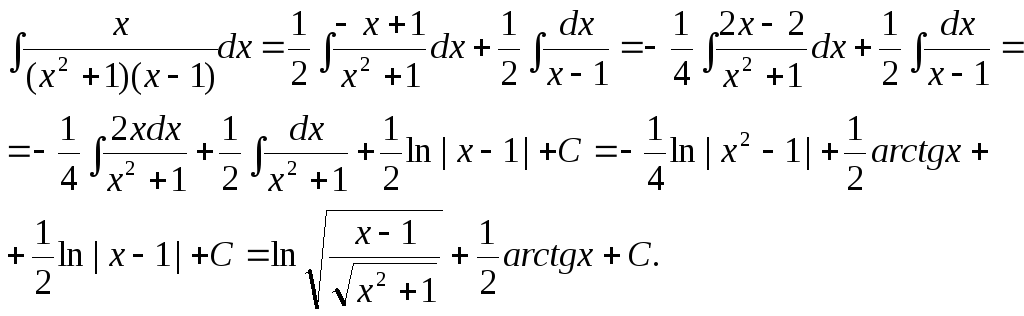
Интегрирование некоторых классов тригонометрических функций

Теорема: Интегралы от рациональных функций относительно тригонометрических функций , , , приводятся к интегралам от рациональных дробей с помощью универсальной тригонометрической подстановки :

Пример 11. Найти .

Решение

Сделаем замену: .

Тогда

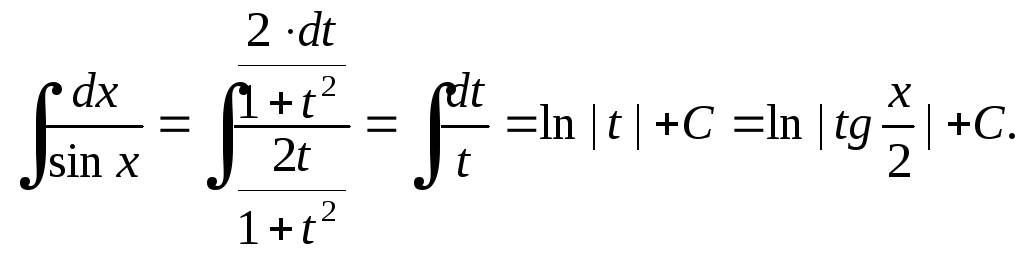
Теорема: Если под знаком интеграла находится функция такая, что или ,

это можно упростить интеграл подстановками или .

Теорема: Если , это можно воспользоваться подстановкой .

Пример 12. Знайти .

Решение

Поэтому пусть , тогда

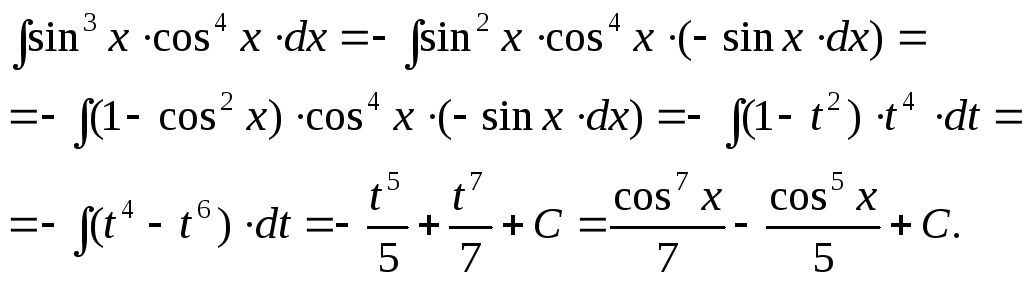
Пример 13. Найти .

Решение:

путь , тогда .

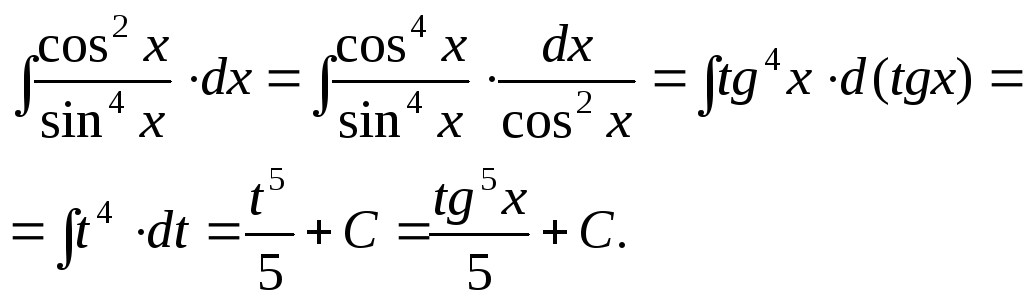
Теорема: Если подынтегральная функция имеет вид: , это произведение можно свести к сумме:

,

,

.

Пример 14. Найти .

Решение

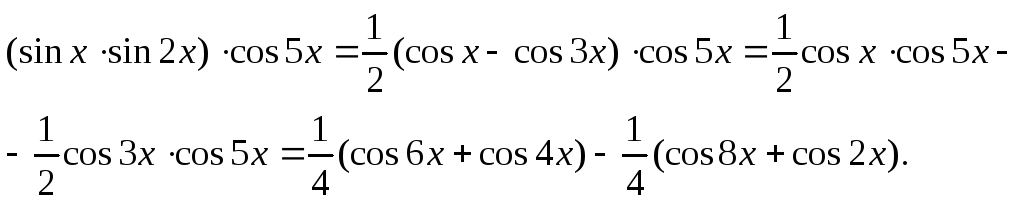
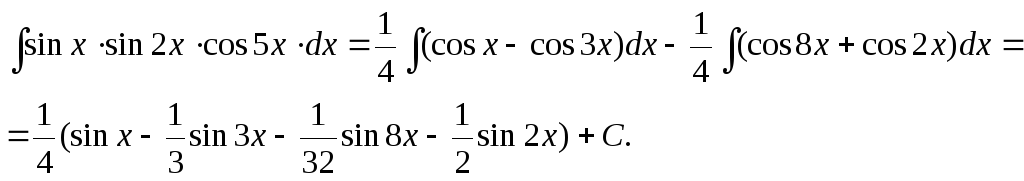
Теорема: Если , находятся под знаком интеграла в четных степенях, то степень можно понижать:

Пример 15. Найти .

Решение:

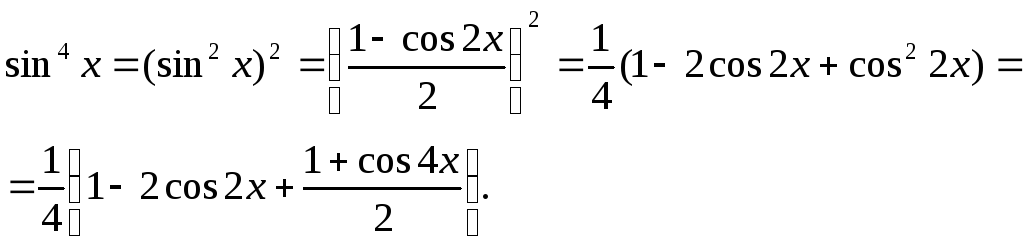
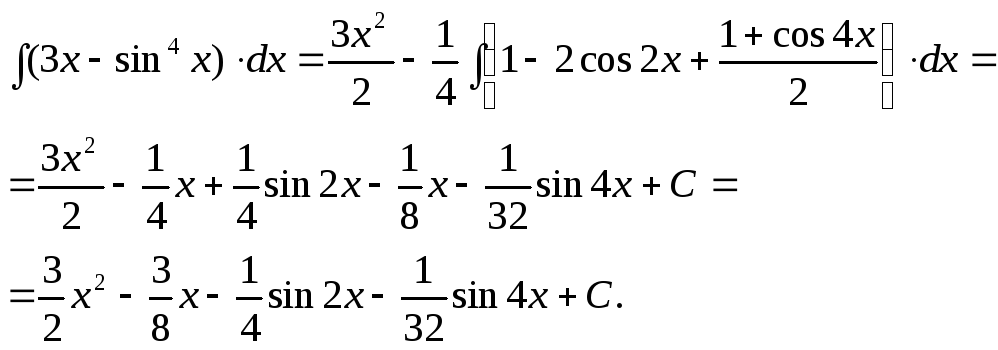
Общее правило интегрирования рациональных дробей.

1. Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби;

2. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей;

З. Проинтегрировать многочлен и полученную сумму простейших дробей.

На практике при вычислении неопределенных интегралов используют различные справочники, содержащие таблицы особенно часто встречающихся интегралов. В частности, «Таблицы неопределенных интегралов» М. Л. Смолянского.

Изученные методы интегрирования позволяют во многих случаях вычислить неопределенный интеграл, т. е. найти первообразную функцию для подынтегральной функции.

Возникает вопрос, для всякой ли непрерывной функции существует неопределенный интеграл и как его найти, если он существует. Ответ на первую часть вопроса дает теорема Коши.

Теорема Коши. Всякая непрерывная функция имеет первообразную. Т.е. для каждой непрерывной на промежутке функции существует , производная от которой на промежутке равняется функции , т.е. .

Тогда существует и неопределенный интеграл

,

где - произвольная постоянная.

Но теорема Коши не дает ответа, как же найти неопределенный интеграл, и не утверждает, что первоначальная функции может быть выражена через конечное число элементарных функций.

В том случае, когда первообразная некоторой элементарной функции f(х) является также элементарной функцией, говорят, что ∫f(х) dх «берется», т. е. интеграл выражается через элементарные функции (или интеграл вычисляется). Если же интеграл не выражается через элементарные функции, то говорят, что интеграл «не берется» (или «его найти нельзя»).

Так, например, нельзя взять интеграл ∫√х∙соsх dх, так как не существует элементарной функции, производная от которой была бы равна √х∙соsх.

Приведем примеры «неберущихся» интегралов, которые имеют большое значение в приложениях:

∫- интеграл Пуассона (теория вероятностей)

- интегральный логарифм (теория чисел)

∫, ∫ - интегралы Френеля (физика)

- интегральный синус и косинус

- интегральная показательная функция

Вычисления таких интегралов возможно с помощью методов приближенного интегрирования, с которыми мы познакомимся позже.