Примеры решения задач

Пример . Тело массой m=2 кг подвешено к упругой пружине, совершает гармонические колебания. Определите жёсткость k пружины, если за время t=1,5мин число N полных колебаний равно 60.

Дано: m=2кг; t=1,5мин=90с; N=60.

Найти: k.

Решение: Период гармонических колебаний тела, подвешенного на пружине (пружинный маятник),

,

где m- масса тела; k- жёсткость пружины.

С другой стороны, период колебаний

,

где t – время, за которое совершается N полных колебаний.

Приравняв оба выражения

Найдём искомую жёсткость пружины

Ответ: k=35,1 Н/м.

Пример . При подвешивании грузов массами m₁ и m₂=2 m₁ к свободным пружинам пружины удлинились одинаково (Δх=15см). Пренебрегая массой пружин, определите: 1) периоды колебаний грузов; 2) какой из грузов при одинаковых амплитудах обладает большей энергией и во сколько раз?

Дано: m₁; m₂=2 m₁; Δх=15см=0,15м; А₁=А₂=А.

Найти: 1) Т₁; Т₂ ; 2) .

Решение. Из условия равновесия грузов на пружине следует, что

m₁g=k₁Δx и m₂g=k₂Δx

(удлинение в обоих случаях одинаково), где k₁ и k₂ – соответственно жёсткость первой и второй пружин. Тогда

и (1)

Периоды колебаний грузов на пружинах соответственно

и (2)

Подставив выражения (1) в формулу (2), найдём

и

т.е. периоды колебаний равны:

.

Механическая энергия груза, колеблющегося на пружине,

(3)

где А – амплитуда колебаний; - циклическая частота.

Поскольку по условию задачи А₁=А₂=А и нашли, что Т₁=Т₂, поэтому искомое отношение энергий, согласно формуле (3),

.

Следовательно, Е₁ в два раза меньше, чем Е₂.

Ответ: Т₁=Т₂=0,776 с; Е₂=2Е₁.

Пример . Один из математических маятников совершил N₁=20 колебаний, другой за то же время совершил N₂=12 колебаний. Определите длины обоих маятников, если разность их длин Δℓ=16см.

Дано: t₁=t₂=t ; N₁=20; N₂=12; Δℓ=16см=0,16м.

Найти: ℓ₁; ℓ₂.

Решение. Период колебаний

,

где t – время, за которое совершилось полных колебаний.

По условию задачи,

N₁Т₁=N₂ Т₂ (1)

где периоды колебаний первого и второго математических маятников

и (2)

(где g – ускорение свободного падения).

Из выражения (1) и (2) следует, что

(3)

Учитывая, что

Δℓ=ℓ₂-ℓ₁ (4)

И решая уравнения (3) и (4), найдём искомые длины математических маятников:

; .

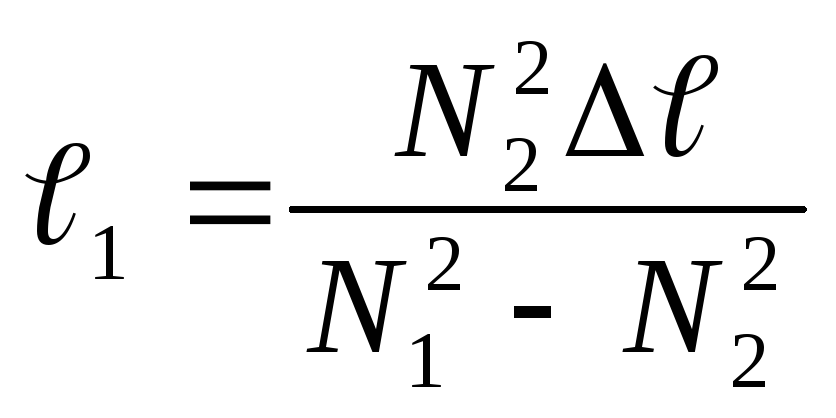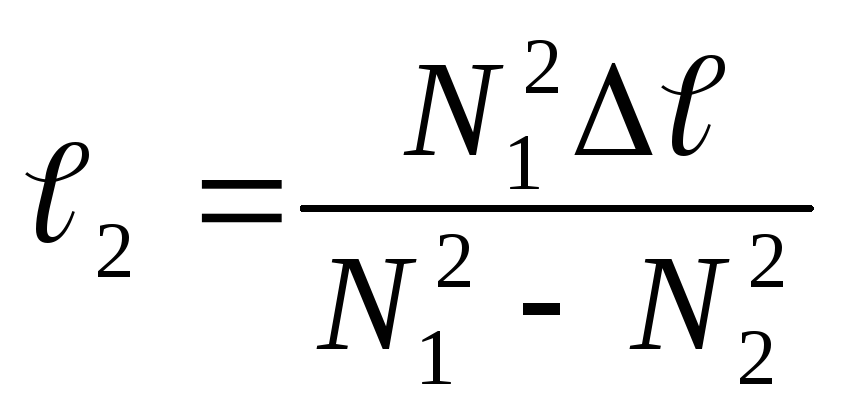Ответ: ℓ₁=9см; ℓ₂=25 см.

Пример . Тонкий обруч подвешен на вбитый в стену гвоздь и совершает гармонические колебания с периодом Т=1,56 с в плоскости, параллельной стене. Определите радиус обруча.

Дано: Т=1,56с.

Найти: R.

Решение. Тонкий обруч под действием силы тяжести совершает колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающую с центром масс. С обруча (см.рисунок).

Это – пример физического маятника.

Период колебаний физического маятника

(1)

где I– момент инерции маятника относительно оси, проходящей через точку подвеса О; ℓ - расстояние между точкой подвеса О и центром масс С маятника; m- масса обруча; g - ускорение свободного падения.

Согласно теореме Штейнера, момент инерции I диска относительно оси не проходящей через его центр масс,

I=I₀+ma²,

г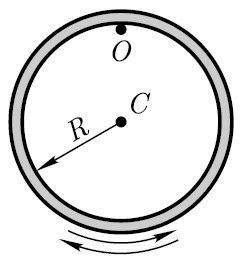деI₀–момент инерции обруча относительно оси, проходящей через центр масс обруча; a- расстояние между осями. Учитывая, что I₀=mR² (тонкостенный диск); а=R, последняя формула запишется в виде

I= mR²+ mR²= 2mR². (2)

Подставив выражение (2) в формулу (1), учитывая, что ℓ=R, найдём искомый радиус диска:

Ответ: R=30,2см.

Пример . Физический маятник в виде тонкого однородного стержня длиной 0,5м совершает гармонические колебания вокруг неподвижной оси, проходящей через точку подвеса О, не совпадающую с центром масс С. Определите, на каком расстоянии х от центра масс должна находиться точка подвеса, чтобы циклическая частота колебаний была максимальна.

Дано: ℓ=0,5 м;ω=ω_max.

Найти: x.

Решение: Период колебаний физического маятника

г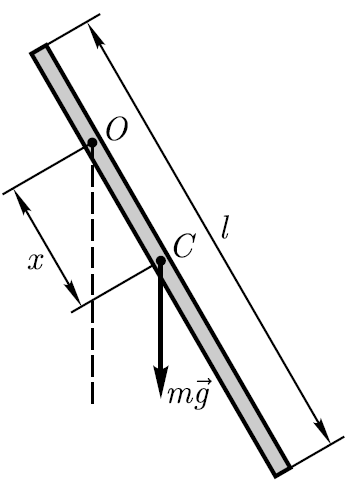деI – момент инерции стержня относительно горизонтальной оси, проходящей через точку подвеса О, не совпадающую с центром масс С стержня (см. рисунок); m - масса стержня; g- ускорение свободного падения; х – расстояние между точкой подвеса О и центром масс С.

Циклическая частота

(1)

Согласно теореме Штейнера, момент инерции стержня относительно оси, проходящей через точку подвеса, находящуюся от центра масс на расстоянии х,

(2)

где -момент инерции стержня относительно горизонтальной оси, проходящей через центр масс стержня (через середину стержня).

Подставив (2) в (1), получим

(3)

Найдём экстремум функции (3) (по условию задачи циклическая частота максимальна):

; ,

откуда

ℓ²-12х²=0

(нас интересуют только положительные решения), т.е. искомое расстояние

Ответ: х=14,4см.

Пример . Материальная точка массой m=10г совершает гармонические колебания с амплитудой А=40см и периодом Т=4с. В начальный момент времени t₀=0 смещение x₀ достигает максимально возможного значения. Запишите уравнение колебаний точки.

Дано: m=10г=10^-2кг; А= 40см; Т=4с.

Найти: x(t).

Решение : Уравнение гармонических колебаний

х=Аcos(ω₀t+φ₀), (1)

где циклическая частота (учли условие задачи); φ₀ - начальная фаза колебаний.

Согласно условию задачи, в момент времени t₀=0 смещение x₀=А (А- амплитуда колебаний). Тогда уравнение (1) можно записать в виде

откуда cos φ₀ =1. Следовательно, начальная фаза φ₀=0.

Используя найденные значения ω₀, φ₀ и заданное А, искомое уравнение колебаний точки:

,м

Пример 6.1. Материальная точка, совершающая гармонические колебания с

частотой ν=1Гц, в момент времени t=0 проходит положение, определяемое координатой x₀=4см, со скоростью υ₀=-16см/с. Определите амплитуду колебаний.

Дано: ν=1Гц; t=0; x₀=4см (4∙10^-2м); υ₀=-16см/с (-16∙10^-2м/с).

Найти: А

Решение :Уравнение гармонических колебаний материальной точки

x=Аcos(ω₀t+φ₀) (1)

где ω₀=2πν.

Скорость точки, совершающей гармонические колебания,

(2)

В начальный момент времени (t=0) смещение и скорость материальной точки, согласно (1) и (2)

х₀=Аcosφ₀ (3)

υ₀=-ω₀Аsinφ₀ (4)

Поделив (4) на (3), получим

откуда

Из формулы (3) амплитуда колебаний равна

Учитывая, что cosφ₀=0, 843, получаем А=4,74 см.

Ответ: А=4,74 см.

Пример . Материальная точка массой m=10г совершает гармонические колебания с частотой ν=0,2 Гц. Амплитуда колебаний равна 5 см. Определите: 1) максимальную силу, действующую на точку; 2) полную энергию колеблющейся точки.

Дано: m=10г=10^-2кг; ν=0,2 Гц; А=5см=5∙10^-2м

Найти: 1) Fmax; 2) E

Решение : Уравнение гармонических колебаний материальной точки

x=Аcos(ω₀t+φ₀) (1)

Тогда скорость и ускорение колеблющейся точки

Согласно второму закону Ньютона, сила, действующая на точку,

F=ma=-Aω₀²m∙cos (ω₀t+φ₀).

F=F_max при cos(ω₀t+φ₀)= ±1, поэтому искомое максимальное значение силы

F_max=Aω₀²m=4π²ν²Am

Учли, что ω₀=2πν.

Полная энергия колеблющейся точки

Подставив сюда ω₀, найдём искомую полную энергию:

Е=2π²mν²A²

Ответ: 1) F_max=0,8мН; 2) Е=19,7мкДж.

Пример . Материальная точка массой m= 5г совершает гармонические колебания с амплитудой А=10см и частотой ν =1Гц. В начальный момент времени t₀=0 смещение x₀=А. Определите кинетическую и потенциальную энергии в момент времени t = 2,2с

Дано: m=5г=5∙10^-3кг; А=10см=10∙10^-2м; ν=1Гц; t₀=0; x₀=А; t = 2,2с.

Найти: Т; П.

Решение : Кинетическая и потенциальная энергии материальной точки, совершающей гармонические колебания,

; (1)

; (2)

где циклическая частота ω₀=2π ν =2π с^-1 (учли условие задачи); φ₀- начальная фаза.

Уравнение гармонических колебаний:

x=Аcos(ω₀t+φ₀)

которое для условий задачи запишется в виде

x=0,1cos(2πt+φ₀),м

Для определения начальной фазы учтём, что при t₀=0 смещение x₀=А. Тогда можем, согласно (3), записать

x₀=0,1cos(2π∙0+φ₀)=0,1 м,

т.е. cosφ₀=1 и φ₀=0. Таким образом, фаза колебаний равна 2πt c^-1.

При заданной фазе колебаний уравнения (1) и (2) примут вид:

;

Ответ: Т=892мкДж; П=94,2мкДж.