t

y(t) h( ) u(t) (t )u( )d ,

где h(t), (t) – переходная и весовая функции динамической системы. Для дискретной системы при T0 1 справедливо

k

y(k) u(i) (k i) ,

i

где (i) – весовая функция импульсной системы.

Для моделирования дискретной возмущающей среды z(k) можно вос-

пользоваться разностным уравнением (3.18), но на вход дискретного динамического звена подать дискретный белый шум с наперед заданными параметрами.

Тогда случайный сигнал можно представить авторегрессионым процессом со скользящим средним

z(k) c z(k ) ... cp z(k p) (3.19)n(k) d n(k p) ... d p n(k p).

Здесь n(k) – последовательность нормально распределенных статиче-

ски независимых случайных величин (дискретный белый шум) с математиче-

ским ожиданием

M n(k)

и ковариационной функцией

cov n(k), ( ) ,

n

где

– дисперсия; ( ) – функция Кронекера

n

при

( )

при 0.

Запишем дискретную передаточную функцию фильтра возмущения в

соответствии с уравнением (3.19) в виде

Gz (z)

z(z)

C z 1

1 c1z 1

... cp z p

.

(3.20)

n(z)

D z 1

1 d z

1

... d

p

z p

1

3.4.Преобразование и исследование динамических моделей

Для перехода от передаточной функции (3.13) к модели пространства состояний используем соответствующее ей дифференциальное уравнение (3.17). Поделим левую и правую часть уравнения (3.17) на коэффициент an при старшей степени производной и получим

112

yn t

a'

yn 1

t ... a'

y t a

' y t

n

2

1

(3.21)

u m t b'

u m 1 t

t b' u t ,

b'

... b' u

m

m 1

1

0

где a'

an

,...,a'

a

, a'

,b'

bm

,b'

bm

,...,b'

b

.

n

an

an

an

m

m

an

an

an

При

нулевых

начальных

условиях

y( ) y' ( ) ... yn ( ) и

u( ) u' ( )

... um ( ) уравнению (3.21) соответствует система уравне-

ний состояния вида (2-я каноническая форма)

						an'
	x					a'
						n
						'
						a
	xn					'
						a

и уравнение наблюдения

				x					b'
									m
				x				b'
									m-1
			x						'
									b
					n-1				1
				xn					b0'

	u,	(3.22)

		x
	y ...	x			,
		xn

где коэффициенты матрицы состояния и вектора связи со входом однозначно определены коэффициентами дифференциального уравнения (3.21).

Связь переменных состояния системы (3.22) с исходными переменными дифференциального уравнения (3.21) определена системой уравнений

x y;
x	y	' a'	y b' u;
		n	m
x	y	'' a'	y' b'	u' a'	y b' u;		(3.23)
		n	m	n		m
x	y n a' y n ... a'					y b'u.
n			n

Уравнения (3.23) используют для определения начальных условий переменных состояния, то есть нахождении вектора начальных условий x .

Отметим, что недостающие коэффициенты в векторе связи со входом b при n m дополняют нулями, начиная с верхних элементов столбца b .

Пример 3.1. Следящая система описывается дифференциальным уравнением второго порядка

. y" y' y . u' u .

113

Перейти к модели пространства состояния. На входе действует единичное ступенчатое воздействие u t t . Начальные условия до приложе-

ния единичной ступенчатой функции равны y y' .

Приведем данное дифференциальное уравнение к уравнению вида (3.21). Для этого поделим левую и правую его часть на коэффициент при старшей производной левой части

y" y' y u' u .

Согласно (3.22) запишем уравнения состояния и наблюдения следящей системы

x

x

	x					u;
	x

	y		x
			.
			x
Начальные условия системы согласно (3.23)
x y ;
x		y' y u .

В случае равенства степеней производной левой и правой частей дифференциального уравнения (3.21) n m уравнения состояния принимают вид (2-я каноническая форма)

				an'
x			an'
x
					'
				a
				a'
xn

а уравнение наблюдения

x

bm' an' bm'

bm' an' bm'

x

u , (3.24)

xn

bm'

a'

b'

bm'

a'

b'

xn

x

b'

y

u .

(3.25)

m

xn

Связь переменных состояния с исходными переменными дифференциального уравнения (3.21) выражается из уравнений (3.25) и (3.24) и определена системой уравнений

114

	x	y b'		u;
			m
	x	y	' b	' u' a'		y b'	u;
			m		n	m		(3.26)
	x	y	n b'		u n a'		y n ... a'	y b'u.
	n			m		n

Коэффициенты матрицы состояния и вектора связи со входом однозначно определены коэффициентами уравнения (3.21). Уравнение (3.26) используют для расчета начальных условий переменных состояния.

В матричной форме уравнения (3.24) и (3.25) имеют вид

x Ax bu;

(3.27)

y cT x du,

где A, b – матрица состояния и вектор связи со входом определяются как и в уравнении (3.24); y – выходная переменная (выход системы); cT c c ...cn

– вектор-строка связи с выходом; d – коэффициент безынерционной связи входа с выходом и согласно (3.25) d bm' .

Системе уравнений (3.27) соответствует структурная схема, представленная на рис. 3.10.

					d
			x(0)
u t		x	t	x		y
	B				сT
			( )d
			0
		+
			A

Рис. 3.10. Структурная схема модели пространства состояний (3.27)

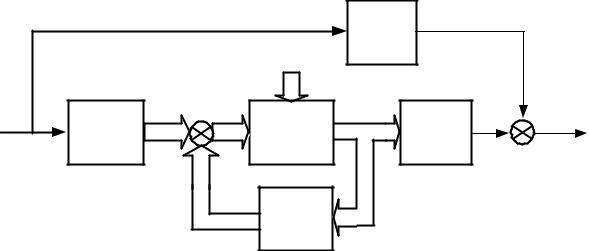
Переход к моделям пространства состояний по структурной схеме системы. Как видно из (3.23) и (3.26) переменные состояния 2-ой канонической формы есть линейная комбинация входных и выходных переменных и их производных. Это затрудняет физическую интерпретацию переменных состояния и реализацию соответствующих регуляторов и обратных связей. Непосредственный переход от структурных схем к моделям пространства состояний устраняет данный недостаток и осуществляется в следующем порядке:

115

1)проводим нумерацию динамических звеньев структурной схемы в порядке i , , ...;

2)обозначаем входные воздействия пронумерованных динамических звенье через ui ;

3)обозначаем выходы динамических звеньев через xi с учетом порядка звена и номером последнего обозначения выхода xi (индекс переменных

состояния должен последовательно увеличиваться от звена к звену); 4) записываем уравнения состояния каждого динамического звена, ру-

ководствуясь табл. 3.1 или правилами перехода от передаточной функции к модели пространства состояний;

5) составляем уравнения для связи входов ui с выходом ему предше-

ствующего i звена непосредственно по структурной схеме;

6) составляем уравнения преобразования нелинейных звеньев. Последовательность перехода рассмотрим на простой модели (рис.

3.11).

1 2

r p

u

K

x

u

K

x

y p

T p

T p

(-)

Рис. 3.11. Структурная схема линейной системы

Таблица 3.1

Уравнения состояния для типовых динамических звеньев

Передаточная функция

Уравнение состояния

K

xi Kui

p

K

Ku

x

xi

i

Tp

T

i

Kui Txi

xi

K

xi

T

T p Tp

xi

xi

116

T T

xi

K

K

T x

x

K T p

T

T

i

i

i

T p T p

x

KT u

xi

i

T

i

T

K T p

T

K

zi

T

ui zi

T p

KT

x

u

z

i

i

i

T

Kui zi

KTp

zi

T

Tp

xi Kui zi

K Tp

K

zi

ui

T

Tp

xi

Kui

zi

Всоответствии с п.1 последовательности пронумеруем динамические звенья (обозначения над звеньями 1 и 2).

Далее обозначим входы и выходы пронумерованных динамических звеньев соответственно u и u и выходы x и x .

Всоответствии с табл. 3.1 имеем

			K			u x ;
x
	T
				K u x .
x
	T

Уравнение связи входов и выходов пронумерованных динамических

звеньев

u r t x ;

u x .

Подставляя уравнения связи в уравнение состояния, получим

x				K r t x x ;
T
					K x x .
x
	T

Уравнение наблюдения согласно структурной схемы y x .

117

В матричной форме уравнения состояния и наблюдения имеют вид (сравни с 3.9)

K

K

x

T

x

T

T

r(t);

K

x

x

T

T

y

x

.

x

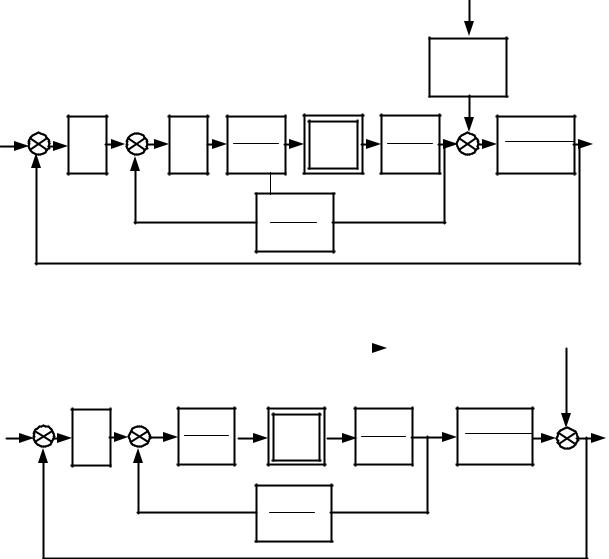
Рассмотрим последовательность перехода для замкнутой нелинейной системы, структурная схема которой приведена на рис. 3.12а.

Поскольку в цепь возмущения p включено звено, порядок числите-

ля которого больше порядка знаменателя, сделаем перенос сумматора через звено и перейдем к структурной схеме, приведенной на рис. 3.12б. Рассмотренная ситуация вряд ли возможна на практике и приведена для иллюстрации вариантов перехода к типовым звеньям.

На структурной схеме (рис. 3.12б) пронумеруем динамические звенья, кроме безынерционных усилителей и сумматоров, входы и выходы звеньев. При обозначении колебательного звена с номером 3 индекс предыдущей выходной переменной x увеличивается на 2, поскольку это звено второго по-

рядка. Следует отметить, что можно не соблюдать последовательность индексации пропускать часть индексов. Но при окончательном формировании уравнений состояния придется проводить переиндексацию переменных, что может привести к ошибкам.

В соответствии с табл. 3.1 составляем уравнения состояния системы управления

		1		K K					u x ,
x1
								4
		T1				1				1		1
			1		K u					x		,
x2
								2			2
			T3			3
			1			K				2 T x x				,
x3							u
		T 2				2		3				2	3	4
		2

118

x4

z5

x5

x6

x7

x3 ,

1 K6u4 z5 , T6

K6u4 z5 ,

1

K K T

t 2 T2 x6

2 T2

x7 ,

K2 K7

2

7

4

T 2

T 2

2

x

K2 K7T4

t .

6

T 2

2

Уравнения связи входов и выходов динамических звеньев u K r t x x x ,

u F x , u x ,

u x .

Подставляя их в уравнения состояния, получаем

x

K K K r t x x K x z x ,

T

K F x

x ,

x

T

K x T x x ,

x

T

x x ,

z

K x z ,

T

K K T

x

K

T

t

T x x ,

T

K

T

K K T

t .

x x

T

119

p

K T p

r p
	K

	K	F	K			y p
K						K
	T p		T p		T p T p
	K T p
	T p

а)	5

p
			K K T p				x
		T p T			p

1

2

3

y p

r p

u

K

K

x

F

u

K

x

u

x

K

K

T p

T p

T p T p

4

x

K T p

u

T p

б)

Рис. 3.12. Структурная схема нелинейной системы а) исходной б) преобразованной

Уравнение выхода согласно структурной схемы y x x .

Нелинейное звено F x должно иметь математическое описание, либо

типовую схему (ограничение, отсечка, люфт и т.п.).

Переход от непрерывных моделей к дискретным.

Рассмотрим переход от непрерывной модели к дискретной различными методами на примере апериодического звена первого порядка.

120

Звено описывается передаточной функцией W p

K

K '

и со-

Tp

p a

ответствующим дифференциальным уравнением первого порядка

Tdy t

y(t) Ku(t),

dt

где a

,

K '

K

.

T

T

Для

непрерывной системы с экстраполятором нулевого

порядка на

входе, передаточная функция непрерывной части системы будет иметь вид

	p W p W p e		pT		K	'
W							,
пн	ф	p			p a
где Wф p – передаточная функция экстраполятора нулевого порядка,								T –

интервал квантования.

Для получения дискретной передаточной функции воспользуемся таблицей z-преобразования [21]

T p

z Z

W p

W z Z W p W p Z

e

W p

ф

p

p

W

p

z

K

'

z

z e

aT

K

'

Z

Z

aT

z

p

z

p p a

z

z z e

a

e aT

K

'

a K

b z

,

z e

aT

a

z a

a z

T

,

где a e T , b K a

z e pT .

В соответствии с (3.16) и (3.18) разностное уравнение будет иметь вид y(k) a y(k ) b u(k ) , или

y(k) b u(k ) a y(k ).

Преобразование Тастина. Преобразование Тастина позволяет рассчитать W (z) без таблиц z-преобразования и основано на приближенном

cоотношении

p			z	.
	T		z

Подставив это выражение в передаточную функцию звена и проведя преобразования получим

W z				K				b	b z
										,
				z				a z
	T T		z
			121

где b

KT

, b

KT

,

a

T T

.

T T

T T

T T

Соответственно разностное уравнение имеет вид

y(k) a y(k ) b u(k) b u(k ) , или

y(k) b u(k) b u(k ) a y(k ) .

Левые разности. Производная аппроксимируется выражением

dy(t)

y(k) y(k )

.

dt

T

После подстановки в дифференциальное уравнение и преобразования

получим

y(k) b u(k) a y(k ) ,

где b

K

, a

a

, a

T

.

a

a

T

Правые разности. Производная аппроксимируется выражением

dy(t)

y(k ) y(k)

.

dt

T

В правых разностях разностное уравнение апериодического звена име-

ет вид

y(k )

K

u(k) ( a) y(k) ,

a

где a

T

.

T

Выбор интервала

квантования T зависит от динамики объекта, от

спектра возмущающих сигналов, от типа измерительных приборов и от ряда других противоречивых факторов. Некоторые рекомендации даны в [21, разд.5.5].

Для задач моделирования и идентификации непрерывного объекта ре-

комендуется такт квантования выбирать из соотношения
T0 1/ 6 1/15 tnn ,	(3.28)

где tnn – время переходного процесса объекта (системы) управления.

Так, для апериодического звена первого порядка, не охваченного об-
ратной связью, время переходного процесса tnn T , следовательно
T				T . . T .

Если апериодическое звено охвачено единичной отрицательной обратной связью, то передаточная функция системы имеет вид

	Wз ( p)	K з		,
		Tз p
	122

	где Kз	K	, Tз	T	.
		K		K

Следовательно, для замкнутой системы

			1		1				3T
	T0									.
			6		15				1 K

Анализ динамических моделей с использованием пакета Control System Toolbox. Пакет предназначен для работы с линейными динамическими, стационарными, непрерывными и дискретными моделями ОУ (Time-Invariant или LTI-модели). Эти модели могут быть как одномерными (SISO – один вход/ один выход), так и многомерными (MIMO – много входов/ много выходов) и задаются в виде:

передаточной функции, tf-модель

W (s)	s2 3s 2	;
	s3 4s2 12s 4

нулей-полюсов и коэффициента усиления, zpk-модель

W (s)	(s )(s )	;
	(s )(s )(s )

пространства состояний, ss-модель

x Ax Bu, y Cx Du.

Здесь в передаточных функциях используется оператор s .
Команды создания LTI-моделей. Строка
			W tf ,
создает tf-модель W(s) s/ s2			2s 10 . При этом MATLAB выводит в ко-
мандное окно сообщение
Transfer Function:
s
--------------------
s^ s
МИМО-модели
B 1	1 ; 1	1	% полином числителя
A 1	2 ; 1	4 5	% полином знаменател я

W tf B, A .

MATLAB отвечает сообщением

Trnasfer function from input to output… s-1

#1: ----------

123

	s+2
	s+1
#2:	------------------ .
	s^2+4s+5
Задавая zpk-модель в виде		2 , 2
	W zpk 0, 1

получим сообщение

Zero/pole/gain:

-2s

------------------ . (s-1)(s-2)

Для создания ss-моделей используют команду sys ss A, B, C, D

что создает модель с именем sys, содержащую матрицы A, B, C, D, которые должны иметь совместимые размерности строк и столбцов.

Для моделей с нулевой матрицей D используют выражение D 0 . Так для ss-модели

sys ss		;			, ;	, ,
имеем
A			, B ,C , D .

Дискретные модели. Для их создания используют те же команды tf, zpk, ss с добавлением в их синтаксис периода квантования T , в секундах

sys tf num, den,T0 sys zpk z, p, k,T0

sys ss A, B,C, D,T0 .

Например, строка команды

Wz tf 1 1 , . , .

задает дискретную модель W (z) (z ) /(z . ) с T0=0.1 сек

Transfer function: z+1

-------- . z-0.5

Sampling time: 0.1.

Дискретная tf функция в DSP формате.

При цифровой обработке сигналов (DSP – Digital Signal Processing) передаточную функцию обычно записывают в виде рационального выражения

124

с использованием z , а числитель и знаменатель содержат коэффициенты

полиномов в порядке возрастания степеней z . Например, числитель и знаменатель выражения

	H z	. z
		z z
	нужно указать как вектора-строки				, а это противоречит
		. и
	обычному правилу уменьшения степеней z .		Чтобы избежать этого, Control

System Toolbox имеет специальную функцию filt для задания DSP формата. Для дискретных передаточных функций вида (3.16) используется команда

Wz filt num,den,T .

Так, строка

Wz . ,

дает ответ

Transfer function: 1 + 0.5 z^–1

-------------------------

1 + 2 z^–1 + 3 z^–2.

Переход от передаточной функции к модели пространства сосотояния и наоборот, осуществляется теми же командами tf, zpk и ss

W tf(sys) W zpk(sys) sys ss W

%преобразование модели sys в tf - модель;

%преобразование модели sys в zpk - модель;

%преобразование модели W в ss - модель.

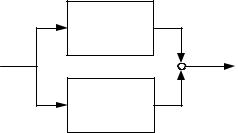
Операции над моделями. Операция сложения соединяет системы параллельно. Так, строка

sys sys1 sys2

возвращает LTI-модель sys с параллельным соединением sys1 и sys2 (рис.

3.13)

sys1

u		y

sys2

Рис. 3.13. Сложение LTI-моделей

Операция умножения соединяет системы последовательно. Так, sys sys1 sys2

125

возвращает LTI-модель sys с последовательным соединением sys1 и sys2 (рис. 3.14)

u			v			y
		sys2			sys1

Рис.3.14. Умножение LTI-моделей

Обратите внимание на обратный порядок следования sys1 и sys2 на структурной схеме (рис. 3.14). Это обусловлено порядком вычислений.

Конкатенация моделей осуществляется матрично-подобным видом:

sys sys1,sys2	% горизонтальная конкатенац ия;
sys sys1;sys2	% вертикальн ая конкатенац ия.

В терминах ввода/ вывода эти две операции имеют следующие блочные интерпретации (рис. 3.15)

	u			y
			H	H
			+ y	u
			+	y
	u
			H	H

Рис. 3.15. Горизонтальная и вертикальная конкатенация LTI-моделей

Запаздывание в непрерывных системах поддерживается MATLAB в пределах совместимости отдельных моделей. Так, для tf-моделей запаздывание (time delay) задается введением в команду строки 'inputdelay' и его значе-

ния. Например, строка	. ,'inputdelay ', .
W tf . ,
приводит к ответу
Transfer function:
		1.5
exp(-0.05*s) * ---------------------------
	s^2 + 14 s + 40.02
Строка		,	,		,'inputdelay ',	.
H tf ,
			126

приводит к ответу

Transfer function from input 1 to output: 1

-----

s+2

Transfer function from input 2 to output: s

exp(-0.2*s) * ----------------------

s^2 + 2 s + 5

Для ss-моделей запаздывание задается аналогично:
sys ss ,	, ; , ,'inputdelay ', .	. % ss-модель, два входа, два

выхода и два значения T .

Переход от непрерывных к дискретным моделям и обратно в пакете

Control System Toolbox. Функция с2d производит дискретизацию непрерывной модели, а функция d2c , наоборот, преобразует дискретную модель в непрерывную. Эти команды поддерживают несколько видов квантования/ восстановления: с экстраполяром нулевого порядка (zoh - Zero-Order Hold), с экстраполяром первого порядка (foh - First-Order Hold), аппроксимацию Тастина без и с предварительной модификацией частот, с согласованием полюсов и нулей. Синтаксис этих команд (с zoh по умолчанию) таков:

	sysd c2d sysc,T	% переход от непрерывной модели sysc к дискретной
		sysd, T - период квантования;
	sysc d2c sysd	% переход от дискретной модели sysd к непрерыв-
		ной sysc.
	Для задания других методов преобразования следует указать их допол-
	нительно:
	sysd c2d sysc,T ,'foh'		% использует foh метод;
	sysc d2c sysd,'tustin'		% использует аппроксимацию Тастина.

Переход от дискретной модели к непрерывной имеет ограничения:

-d2c с zoh преобразованием не может оперировать с моделями, имеющим полюса z ;

-действительные отрицательные полюса в z-области отображаются в два комплексных полюса в s-области, что ведет к увеличению порядка непрерывной системы.

Функция с2d может также квантовать непрерывные системы с запаздыванием, однако при этом используют только методы zoh и foh. Так, для дискретизации системы с передаточной функцией

W s e . s		,

s s

если набрать

127

W tf ,		,'inputdelay ', .
Wz c2d W,		. .
MATLAB ответит
Transfer function:

0.01187 z^2 + 0.06408 z + 0.009721 z^(-2) * ----------------------------------------------

z^3 - 1.655 z^2 + 0.7408 z

Sampling time: 0.1

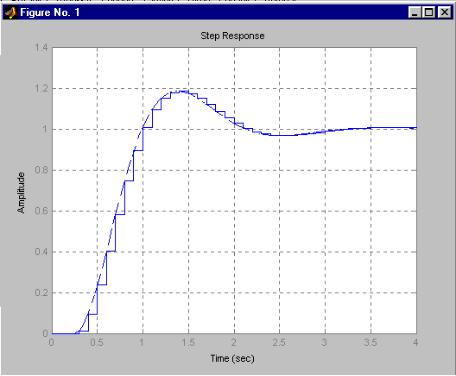
Для сравнения отклика непрерывной и дискретной моделей используем

команду

step W,' ', Wz,' ' .

MATLAB построит график, показанный на рис.3.16.

Рис. 3.16. Переходные процессы систем с запаздыванием

Изменение интервала дискретизации. Дискретную LTI систему sys1

можно подвергнуть квантованию с другой частотой, используя команду

sys2 d2d sys ,T .

Новый интервал квантования T может не отличаться в целое число раз

от прежнего значения.

Для снятия точных значений точек графика достаточно щелкнуть левой кнопкой мышки на интересующей точке и MATLAB выведет название сис-

128

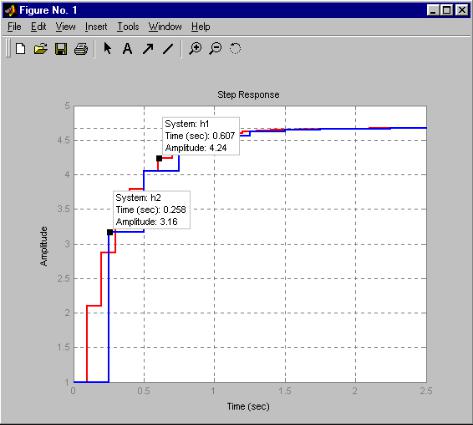
темы, значения по осям ординат и абсцисс (в данном случае – значения времени и амплитуды сигнала отклика системы (рис.3.17)).

Для создания дополнительных текстовых поясняющих надписей на графиках, редактирования толщины и стиля линий, шрифтов можно использовать специальный редактор, который вызывается выбором опции Edit Plot в

меню Tools (Инструменты), опций Arrow, Line, Text, Title, Legend и других в меню Insert (Вставка).

Для ускорения доступа к этим опциям на панели графика имеются кнопки Edit Plot, Insert Arrow, Insert Line, Insert Text. В режиме Edit Plot необ-

ходимо щелкнуть левой кнопкой мыши по нужному элементу и он становится доступным для редактирования. Поэкспериментируйте с этими средствами самостоятельно на графике.

Рис. 3.17. Получение точных данных по графикам

Обратная связь. Для создания отрицательной обратной связи двух моделей sys1 и sys2 используют команду sys feedback sys1,sys2, или экви-

валентную sys feedback sys1,sys2 .

Для создания положительной обратной связи этих моделей используют команду sys feedback sys1,sys2, 1 .

129

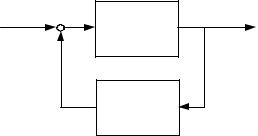
Для ss-моделей опцией feedin указывают какие входы модели sys2 подключены к входам модели sys1, опцией feedout - какие выходы модели sys подключены к входам sys1. Создадим систему, показанную на рис. 3.18.

момент +	W	скорость
-

H

Рис. 3.18. Система с обратной связью

Для этого соединим объект управления

				s s
				W (s) s s
с контроллером в обратной связи
				H (s) (s ) ,
				s
используя команды
W tf		,		,'inputname','момент','outputname','скорость' ;
				H zpk , , ;
				Ws feedback W, H

MATLAB ответит

Zero/pole/gain from input "момент" to output "скорость": 0.18182 (s+0.2192) (s+2.281) (s+10)

------------------------------------------------

(s+3.419) (s^2 + 1.763s + 1.064).

В результате получаем zpk модель Ws в соответствии с правилами предпочтения ss zp tf .

Анализ модeлей. Пакет Control Toolbox имеет команды для определения нулей и полюсов системы, усиления в области низких частот (на постоянном токе) и т.д. (табл. 3.2).

130

	Таблица 3.2
	Команды для исследования динамики систем
covar	ковариация отклика на белый шум
damp	собственная частота и коэффициент демпфирования
dcgain	усиление на низкой частоте (постоянном токе)
dsort	ранжирование полюсов и нулей дискретной системы в поряд-
	ке убывания их модулей
esort	ранжирование полюсов и нулей непрерывной системы в по-
	рядке убывания их действительных частей
norm	нормы LTI моделей (H2 и L )
pole, eig	полюса системы
pzmap	карта полюсов/нулей
tzero	нули системы

Пример использования этих команд для анализа системы h = tf([4 8.4 30.8 60],[1 4.12 17.4 30.8 60])

Transfer function:

4 s^3 + 8.4 s^2 + 30.8 s + 60

---------------------------------------

s^4 + 4.12 s^3 + 17.4 s^2 + 30.8 s + 60 pole(h)

ans =
-1.7971 + 2.2137i
-1.7971 - 2.2137i
-0.2629 + 2.7039i
-0.2629 - 2.7039i
tzero(h)
ans =
-0.0500 + 2.7382i
-0.0500 - 2.7382i
-2.0000
dcgain(h)
ans =
1
[ninf,fpeak] = norm(h,inf)	% peak gain of freq. response
ninf =
1.3402	% peak gain
fpeak =
1.8537	% frequency where gain peaks
	131

Для анализа ss-моделей используют команды из табл. 3.3.

Таблица 3.3

	Команды для анализа SS моделей
canon	каноническая SS реализация
ctrb	матрица управляемости
ctrbf	матрица управляемости в лестничной форме
gram	граммианы управляемости и наблюдаемости
obsv	матрица наблюдаемости
obsvf	матрица наблюдаемости в лестничной форме
ss2ss	линейное преобразование переменных состояния
ssbal	масштабирование с помощью диагональной матрицы

Расчет переходных процессов. Для этого используются команды, описанные в табл. 3.4.

Таблица 3.4

	Команды для получения временного отклика систем
step		реакция на ступенчатое воздействие
impulse		реакция на импульсное воздействие
gensig		генерация входных сигналов
lsim		реакция на произвольное заданное воздействие
initial		реакция на ненулевые начальные условия

Функции step, impulse, initial автоматически выбирают пределы по оси абсцисс для построения переходных процессов. Их синтаксис таков:

step(sys)

impulse(sys)

initial(sys,x0) % x0 – вектор начальных значений переменных состоя-

ния.

Для MIMO систем эти команды строят несколько графиков, по одному на каждый канал входа/ выхода.

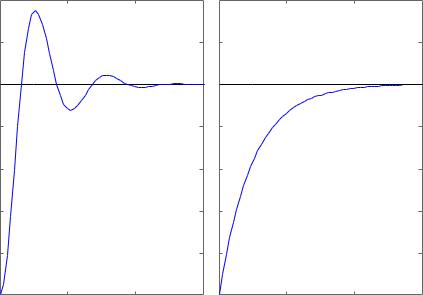
Так, строка:

h = [tf(10,[1 2 10]) , tf(1,[1 1])]; step(h)

строит два графика, показанные на рис. 3.19.

132

Step Response

From: In(1)

	1.4
	1.2
	1
Amplitude	0.8
	0.6
	0.4
	0.2
	0	0	2	4	6	0
					Time (sec)

From: In(2)

2

4

6

Рис. 3.19. Переходные процессы MIMO системы

Автоматический режим выбора пределов времени на графиках можно отменить, задав конечное значение времени:

step(sys,10) % моделирование от 0 до 10 с

или вектор равномерно распределенных значений времени отсчета:

t = 0:0.01:10	% отсчет осуществляется каждые 0.01 секунд
step(sys,t)

Функция lsim строит отклик системы для более широкого класса входных воздействий. Так, команда

t = 0:0.01:10; u = sin(t); lsim(sys,u,t)

рассчитывает отклик LTI-модели sys на синусоидальное воздействие в течение 10 секунд.

Анализ в частотной области. Он позволяет исследовать поведение LTI-модели в частотной области и определить полосу пропускания, резонансную частоту, коэффициент усиления на постоянном токе, АЧХ и ФЧХ, устойчивость замкнутой системы. Для этого используют команды, описанные в табл.3.5.

133

	Таблица 3.5
	Команды для получения частотного отклика систем
bode	диаграмма Боде - ЛАЧХ и ЛФЧХ
nyquist	частотный годограф Найквиста - АФХ
nichols	частотный годограф Никольса - АФХ в угловых координатах
ngrid	линии сетки для диаграммы Никольса
evalfr	частотная характеристика на заданной частоте
freqresp	частотная характеристика в заданном диапазоне частот
margin	запас устойчивости по фазе и модулю
sigma	частотные характеристики сингулярных значений ПФ

В этих командах диапазон частот выбирается автоматически в зависимости от расположения нулей и полюсов системы. Для задания частотной области точно в интервале {wmin, wmax} используют такой синтаксис команд

bode(sys,{wmin, wmax})

рисует диаграмму Боде в диапазоне частот от 0.1 до 100 рад/с. Можно также задать вектор интересующих частот. Например,

w = logspace(-1, 2, 100)

bode(sys, w) .

Команда logspace задает вектор w логарифмически распределенных частот, начиная с 10-1 = 0,1 рад/с и заканчивая 102 =100 рад/с, всего 100 точек.

Построение графиков откликов нескольких систем. Для того, чтобы построить отклики нескольких систем на одном графике, набирают необходимую функцию с входным перечнем исследуемых моделей sys1, ..., sysN:

step(sys1,sys2,...,sysN) impulse(sys1,sys2,...,sysN)

...........

bode(sys1,sys2,...,sysN)

nichols(sys1,sys2,...,sysN)

Все модели должны иметь одинаковое число входов и выходов. Для облегчения восприятия графиков можно задать цвет/ стиль линии/ маркер (color/ linestyle/ marker) для каждой модели также, как и в предыдущих командах - перечислением. Так, команда bode sys1,'r',sys2,' y ',sys3,'gx' строит

график для sys1 непрерывными красными (r - red) линиями, для sys2 - желтыми (y - yellow) пунктирными линиями, для sys3 - зелеными (g - green) ли-

ниями с х маркерами. Можно также задавать и другие цвета, маркеры, толщину линий и т.п.

134

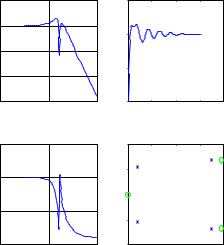
Изменение графиков. Данные откликов системы в частотной или вре-
менной областях можно сохранить в массивах MATLAB командами с лево-
сторонним синтаксисом:
[y,t] = step(sys)		% значение, время
[mag,phase,w] = bode(sys)	% амплитуда, фаза, частота
[re,im,w] = nyquist(sys)		% реальная, мнимая часть, частота.
Сохраненные данные можно использовать для построения графиков в
удобном для пользователя виде. Так, следующий набор команд строит диа-
грамму Боде, переходную характеристику и карту расположения полю-
сов/нулей в одном графическом окне:
h = tf([4 8.4 30.8 60],[1 4.12 17.4
30.8 60])			Bode Magnitude (dB)			Step Response
		10			1.5
[mag,phase,w] = bode(h)		0
					1
[y,t] = step(h,15)
		-10
[p,z] = pzmap(h)
					0.5
		-20
% Bode Plot
subplot(221)		-30 -2	0	2	00	5	10	15	20
semilogx(w,20*log10(mag(:))),		10	10	10
			Bode Phase (deg)			Pole-Zero Map
grid on		50			4
title('Bode Magnitude (dB)')		0			2
subplot(223)
					0
semilogx(w,phase(:)), grid on		-50			-2
title('Bode Phase (deg)')		-100 -2			-4
% Step response			0	2		-1.5	-1	-0.5	0
		10	10	10	-2
subplot(222)
plot(t,y)
title('Step Response')
% Pole/zero map		Рисунок 3.20. Характеристики системы
subplot(224)
plot(z,'go'), hold, plot(p,'bx')
title('Pole-Zero Map')

Можно заменить в представленном перечне команд в строках, начинающихся со слова title (наименование), англоязычные термины их русскими эквивалентами - Амплитуда, Фаза, Переходная характеристика, Карта полюсов /нулей.

Пример 3.2. Рассмотрим непрерывный объект, структурная схема которого представлена на рис. 3.11, для передаточных функций

	W ( p)				, W ( p)			.
		p				p

Передаточная функция разомкнутой системы

135

W ( p) .

p p

Используя z-преобразование для системы с экстрополятором нулевого порядка, перейдем к дискретной передаточной функции

	b z b z
W (z)					,
	a z a			z

где численные значения коэффициентов зависят от такта квантования T .

Воспользуемся результатами z-преобразования [21, табл.3.7.2], для

T с

W (z)	. z . z
		.
	. z . z

Коэффициент усиления разомкнутой системы

K			. .	. .
	z
			. .	.

Преобразование Тастина дает другой результат

WT (z) . . z . z ,. z . z

а коэффициент усиления

Kz . ..

Соответственно для T c

W (z)		. z . z
			,
		. z , z
W (z)	. . z . z			.
		. z . z

Замкнутой системе (см. рис. 3.11) соответствует передаточная функция

	Wз ( p)					,
		p p			p p

с коэффициентом усиления Kз / .

Проведем исследование свойств рассмотренной непрерывной и дискретной модели объекта управления в системе MATLAB с помощью пакета расширения Control System Toolbox (рис. 3.21).

Для контрольной печати введенных передаточных функций и результатов преобразований (вычислений) необходимо удалить завершающий символ командной строки точку с запятой (поэкспериментируйте).

Проанализируем некоторые полученные результаты преобразований. Примечание: скопировать рис. 3.21 в Matlab, выполнить графики.

136

%Пример 3.2

W1=tf(1,[10 1]);% ПФ звена 1 W2=tf(1,[5 1]);% ПФ звена 2

W=W2*W1; % ПФ разомкнутой системы WS=feedback(W,1); % ПФ замкнутой системы

SSR=ss(W);% уравнения состояния разомкнутой системы

ZPR=zpk(W);% zpk-модель

SSK=canon(SSR);% каноническая (диагональная) форма уравнений состояния tzero(W);% нули

pole(W);% полюса

dcgain(W);% коэффициент усиления, приведенный

[mag,phase,w]=bode(W,{0.01,100}); % формирование массива для построения

%ЛАЧХ и ФЧХ

[p,z]=pzmap(W); % формирование массива для построения карты полюсов/нулей

Wz=filt([0 0.00906 0.00819],[1 -1.72357 0.74082]);% ПФ дискретной системы

%по таблице z-преобразований,Т0=1

Wz1=c2d(W,1); % переход от W к WZ, Т0=1 WzT=c2d(W,1,'tustin');% переход от W к WZ по Тастину, Т0=1

SSD=c2d(SSR,1);% переход к дискретной ss-модели, Т0=1 Wz4=c2d(W,4);% переход к дискретной ПФ, Т0=4 WT=d2c(Wz1);% переход от дискретной ПФ к непрерывной

WT1=d2c(WzT);% переход от дискретной ПФ по Тастину (Т0=1) к непрерывной WT4=d2c(Wz4);% переход от дискретной ПФ (Т0=4) к непрерывной %Построение ЛАЧХ и ФЧХ

subplot(221)

semilogx(w,20*log(mag(:))), grid on

title('Амплитуда L(dB)') subplot(223) semilogx(w,phase(:)),grid on title('Фаза(град)')

%Переходной процесс для передаточных функций subplot(222)

step(W,WS,Wz,Wz1,Wz4,100),grid on %расчет п/п title('Переходной процесс для ПФ') %Переходной процесс для уравнений состояния subplot(224)

step(W,SSR,SSK,SSD,100),grid on

title('п.п для уравнений состояния T0=1c')

Рис. 3.21. Программа преобразования и исследования динамической модели

Так, переход от передаточной функции разомкнутой системы к уравнениям состояния дает следующий результат

x .

.x

. x				.
					u ;
	x

y	x
			.
	.
	x

Соответственно zpk-модель имеет вид

.

W ( p) s . s . .

137