Каноническая (диагональная) форма уравнений состояния

		.
x
x

	x			.
					u ;
. x				.

y .

x

.

.

x

Полученные передаточные функции с помощью команды c2d (см. рис.

3.21) совпадают с приведенными в [21, табл. 3.7.2].

Дискретная модель уравнений состояния для T c имеет вид

x (k 1)

0.7326

0.1378

x (k)

0.4305

1

1

u(k) ;

0.1076

0.9909

0.0283

x2 (k 1)

x2

(k)

y (k)

x (k)

.

.

x (k)

Обратный переход от дискретной передаточной функции к непрерыв-

ной для T c и T c дает

W ( p)

.

,

p . p .

что совпадает с искомой W ( p) .

Переход от передаточной функции, полученной по Тастину, дает

W ( p)

. p . p .

.

T

p . p .

В числителе появился полином, но переходной не будет отличаться от искомой W ( p) (проверьте).

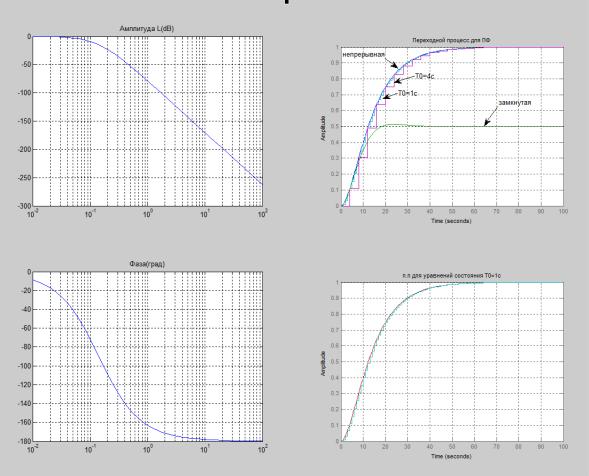
ЛАЧХ и ФЧХ приведены на рис. 3.22.

Переходной процесс для непрерывной разомкнутой и замкнутой системы и дискретной моделей приведены на рис. 3.22. В замкнутой системе время переходного процесса и коэффициент усиления уменьшаются, очевидно также влияние T на переходной процесс.

3.5. Статические модели

Во многих практических задачах управления и проектирования зависимость между выходными и входными переменными (3.1) статическая.

Следовательно, нас не интересует за счет каких входных воздействий объект управления (проектирования) перешел в состояние х(t) , а интересуют

только количественные соотношения выходных переменных y от состояния объекта управления (проектирования).

138

	Статическую зависимость будем представлять в виде
		y Q(x) V ,	(3.29)
где y	– рассчитываемый или наблюдаемый (измеряемый) выходной показа-
тель,	скаляр; Q(x) –	наперед заданная статическая зависимость (функция)
входных переменных;		x x1, x2 ,...,xn	– вектор входных переменных раз-

мерности n 1; v – аддитивная помеха, как результат воздействия всех неучтенных возмущений в модели (3.1).

Рис. 3.22. Исследование динамической модели

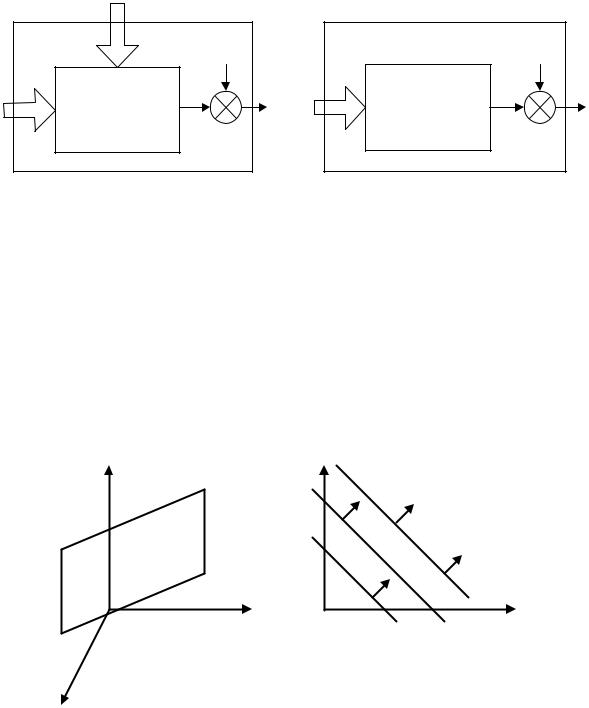
Вектор входных переменных x отражает и входные воздействия ui , zi и состояния xi . Так исходную модель

F(u,z) a0 a1u1 a2 z1 a3u12 ,

легко привести к виду

Q(x) a0 x0 a1x1 a2 x2 a3 x12 ,

где x – фиктивная переменная, x u , x z . Изложенный переход иллюстрирует рис. 3.23.

139

z
ОУ			ОУ
	v		v
u		y	x	y
F (u, z)			Q(x)
а)			б)
Рис. 3.23. Структурная схема статической модели ОУ: а) исходная; б) приведенная

Рассмотрим некоторые часто применяемые модели. Модель или полином первого порядка

n
Q(x) aT x ai xi a0 x0 a1x1 a2 x2		... an xn .	(3.30)
i 0
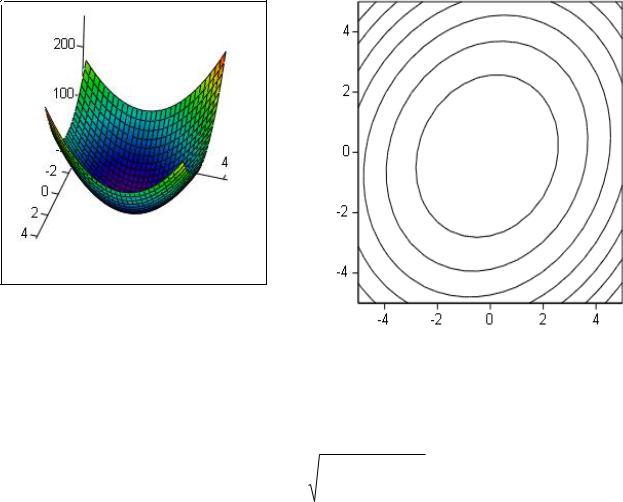
Эта модель линейна относительно переменных		xi , линейна относи-
тельно параметров (коэффициентов)	ai и в n-мерном пространстве представ-
ляет гиперплоскость (рис. 3.24).
Q(x)	x2

gradQ(x)

x1	x1

x2

Рис. 3.24. Линейная модель и ее линии равного уровня

Модель второго порядка или полный квадратичный полином

n	n n
Q(x) aT x X T Ax ai xi aij xi x j ,		(3.31)
i 0	j 1 i 1

140

		a		a	...	a
						n
где	A			a	...	a n		– квадратичная матрица коэффициентов
					...	...
								размерности n n .
		... ...
					...
						ann

Так для n и n матрица А имеет вид

a		a			a		a		a
				A			a		a
A		;								.
		a							a
Соответственно модели

Q(x) a x		a x		a	2	x	2	a	x2	a	x x	2	a	22	x2	,	(3.32)
0	0	1	1					11	1	12	1				2

		Q(x) a			0	x	0	a x a					2		x		2		a x a x2					a x x		2
										1	1								3	3		11	1	12	1		(3.33)
		a		x2 a x x a										x				x a x2 .
			22									23				2
				2			13		1	3									3	33	3
Здесь x x	j	– взаимодействие переменных,																				x	– квадратичные члены
i																						ii
полинома (модели), xi				– линейные члены модели,																		a x		– свободный коэффи-
циент модели.
Модель (3.31) нелинейна относительно переменных xi , но линейна от-
носительно параметров ai , aij , aii .
Если матрица A положительно определена, кроме начала координат

x 0 , т.е. все диагональные определители матрицы A строго положительны

D a ;			D		a		a	;...
							a
	a	a	...	a k
D		a	...	a k		;		D ,
k	... ... ... ...							n

... akk

то квадратичная форма имеет минимум.

Если матрица A отрицательно определена повсюду, кроме начала координат, т.е. выполняются следующие условия

D ;	D	; D	;...( )n D ,
			n
то квадратичная форма имеет максимум.
Положительно и отрицательно определенные квадратичные формы в
пространстве переменных	xi	имеют	поверхности равного уровня

q x , x ,...,xn const в виде концентрических эллипсоидов с центром в начале координат. Линейные члены aT x модели (3.31) не изменяют формы по-

141

верхностей равного уровня, а лишь смещают их в пространстве переменных, не меняя при этом ориентации главных осей эллипсоидов.

Пример квадратичной модели приведен на рис. 3.25.

S

Q

Рис. 3.25. Квадратичная модель и ее линии равного уровня

Некоторые часто используемые в задачах оптимизации квадратичные модели.

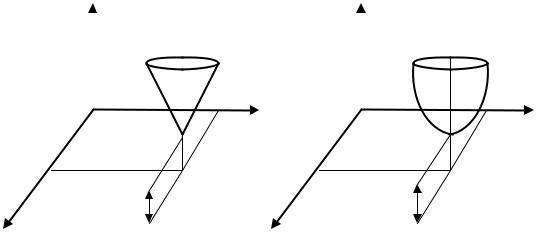
Центральная модель с постоянным градиентом (рис. 3.26, а)

		n
	Q(x) Q*	a1 xi xi* 2	(3.34)
		i 1
и центральная модель с переменным градиентом (рис. 3.26, б)
		n
	Q(x) Q* a1 xi xi* 2 ,		(3.35)
		i 1
где x*	– координаты экстремума по i -ой переменной, Q*		– экстремальное
i

значение функции.

142

		Q(x)				Q(x)
			x*			x*
			1			1
				x1		x1
x2*
			x*	x2*		x*
		Q	*			Q*
x					x2
	2
			а)			б)

Рис. 3.26. Центральные модели второго порядка: а) с постоянным градиентом (конус); б) с переменным градиентом (параболоид вращения)

Эллиптическая модель

Q(x) Q* n a x x* 2 .

i i i

i 1

Сепарабельная модель

Q(x) Q* n f x x* ,

i i i

i 1

где fi ( ) – некоторые наперед заданные функции.

(3.36)

(3.37)

Нестационарность статической модели отражается изменением коэф-

фициентов модели, например
Q(x,t) aT (t)x .	(3.38)

В задачах оптимизации рассматривают частные случаи нестационарности модели, а именно: вертикальный и горизонтальный дрейф экстремальной точки (цели) либо их сочетание. Так, уравнение

	n	it 2
	Q(x,t) a0t ai xi		(3.39)
	i 1
задает вертикальный дрейф экстремального значения функции Q* со скоро-
стью a	и горизонтальный дрейф координат экстремума со скоростью i
(рис. 3.27).

143

Q ( x )

Q*(t2 )

		x* (t )		x* (t	2	)
		1	1	1
		x2* (t1 ) Q*(t )
	*	1				x
x		(t2 )
	2					1

x

2

Рис. 3.27. Пример дрейфа

Модель вида				x* Rsin t 2			x		x* Rcos t 2
Q(x,t) a t x								2			(3.40)
0			1	1					2
задает восхождение параболоида вращения по цилиндру (рис. 3.28).
x2* (t )		x2	R				Q(x,t)

x1* (t )

x1

x1

x2

Рис. 3.28. Пример нестационарной модели второго порядка

Модели нелинейные относительно и переменных xi , и параметров ai , имеют вид

Q(x)		a0 x0 a1x1							,		(3.41)
	a	2	x	2	a	x x		2
					12	1
Q(x) a0 x0							a1x1				(3.42)
					exp					.
						a2 x2

144

Для испытания эффективности алгоритмов оптимизации применяют тестовые функции, имеющие сложные поверхности с характерными острыми

и затяжными «оврагами» и «гребнями». Среди них выделяют.
Овраг Розенброка
Q(x) 100 x2 x12	2 1 x1 2 ,	(3.43)
с координатами минимума Х * ( ; ) .
Функция Пауэлла
Q(x) x1 10x2 2 5 x3 x4 2 x2 2x3 4 10 x1 x4 4 ,		(3.44)
с координатами минимума Х * ( ; ; ; ).
Двумерная экспоненциальная функция
1	2
Q(x) exp ax1 exp ax2	exp a exp 10a	, (3.45)

a 0

где a a . – шаг изменения параметра. Координаты экстремума Х * ( ; ) .

Временные ряды. Для целей прогнозирования наблюдаемых процессов и явлений во времени (прогноз температуры, давления, скорости движения, уровня шума, выпуска продукции, спроса и т.п.) применяют модели:

полином нулевого порядка

x(t) a ,						(3.46)
полином первого порядка
x(t) a a t ,						(3.47)
полином второго порядка
x(t) a		a t	a		t ,	(3.48)
полином n -ой степени как обобщение полиномиальных моделей
n
x(t) aiti ,						(3.49)
i
гармоническую модель для описания периодических процессов
x(t) xm sin( t ).						(3.50)

В экономических задачах часто используют экспоненциальную (показательную) модель

x(t) a tb с ,			(3.51)
и логистическую кривую
x(t)	a	,	(3.52)
	bexp( at)

где a , a, b – параметры (коэффициенты) модели.

Если измерения ведутся в дискретные моменты времени, то подстанов-

145