4.5. Идентификация параметров динамических моделей

Первые реализованные в системах управления методы идентификации динамических объектов типа «вход-выход» были основаны на использовании частотных, ступенчатых и импульсных воздействий. Эти методы требуют специально спланированных входных сигналов, а именно ступенчатых сигналов для идентификации по переходной функции, импульсных входных сигналов для идентификации по весовой функции и синусоидальных входных сигналов с различными частотами для определения частотной характеристики. Большинство этих методов применимы для линейных процессов и частично для линеаризованных и основаны на преобразовании Фурье.

Другой подход идентификации линейных процессов (динамических объектов) использует методы корреляционных функций. При этом на вход объекта подается белый шум с относительно малой амплитудой, накладываемый на рабочий входной сигнал. Некоторые соотношения, связывающие характеристики динамической системы с корреляционными функциями, приведены в разделе 1.8., а практические аспекты их вычисления в разделе

2.9.

Спектральные соотношения входных и выходных сигналов также можно использовать для идентификации параметров частотных функций динамических процессов. Взаимосвязь спектральных плотностей случайных процессов на входе и выходе динамического объекта с его частотной характеристикой приведена в разделе 1.8., а практические аспекты вычисления в разде-

ле 2.10.

Подробно с перечисленными подходами можно ознакомиться в [18, 19,

20].

В настоящее время для идентификации динамических процессов широкое применение нашли методы регрессионного анализа (метод наименьших квадратов), методы стохастической аппроксимации и последовательного обучения, метод квазилинеаризации, градиентный метод с прогнозом, эвристические методы идентификации [19].

Рассмотрим методы идентификации динамических объектов, основанные на регрессионных процедурах с использованием метода наименьших квадратов.

Алгоритмы этих методов ничем не отличаются от алгоритмов идентификации статических объектов, рассмотренных в разделе 4.2. и 4.3.

При изложении материала использована методология [21].

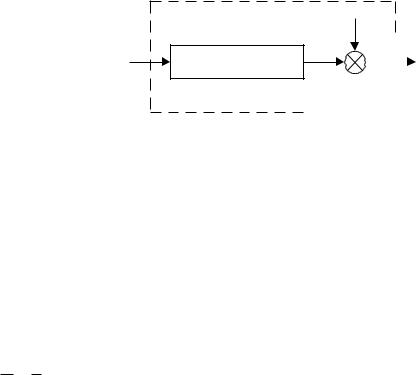
Рассмотрим одномерный дискретный динамический объект (рис. 4.4). Переход от непрерывных моделей к дискретным представлен в разделе 3.4.

196

U (k)

Динамика

объекта

V (k)

X (k)

Y (k)

Рис. 4.4. Одномерный динамический объект

Модель объекта представим в виде разностного уравнения

x(k) a1x(k 1) ... an x(k n) b1u(k d 1) ... bmu(k d m),					(4.75)
и уравнение наблюдения
y(k) x(k) v(k) ,
где
u(k) U (k) U					(4.76)
y(k) Y (k) Y

центрированные переменные; U (k), Y (k) – абсолютные сигналы входа и вы-

хода, U , Y – установившиеся значения входа и выхода.

Следовательно, переменные u(k) и y(k) являются вариациями абсо-

лютных сигналов относительно установившихся значений.

Величина d определяет запаздывание, равное целому числу тактов квантования.

Неизмеряемую вариацию выходной переменной x(k) подставим в

уравнение наблюдения и получим

y(k) a1x(k 1) ... an x(k n) b1u(k d 1) ... bmu(k d m) Vk . (4.77)

Выражая в (4.77) аналогично остальные значения x(k 1), x(k 2) ,…, x(k n) через наблюденные значения y(k 1) , y(k 2) ,…, y(k n) , получим

y(k) T (k) (k ) V (k) ,

(4.78)

где y(k) – наблюденное (измеренное) значение вариации выходной перемен-

ной; ψT (k) y(k 1) y(k 2)...y(k n) u(k d 1)...u(k d m)

(4.79)

– вектор-строка наблюденных значений вариаций выходной переменной и входного воздействия, размерности (n m) 1 ; θT (k 1) a1a2 ...an b1b2bm – вектор-строка неизвестных параметров модели (4.75) на (k ) такте измерений, размерности 1 (n m) .

Структура строки (4.79) повторяет структуру правой части уравнения (4.77) при замене x(k) наблюдением y(k) , x(k 1) соответственно y(k 1) и

197

т.д.

Допустим, что измерения выполнены на интервале k 1,2,...,n d N . Результаты эксперимента представим согласно (4.78) в векторно-матричной форме

	Y (n d N) ψ(n d N)θ(n d N 1) V (n d N),									(4.80)
где
				y(n d )
				y(n d 1)
	Y (n d N )					;				(4.81)
			y(n d N )
			y(n d 1)		y(n d 2)		y(d )
			y(n d )		y(n d 1)		y(d 1)
(n d N )
					y(n d N 2)		y(N d )
		y(n d N 1)
	u(m 1)		u(m 2)		u(0)
			u(m 1)
	u(m)				u(1)					(4.82)
u(m N 1)			u(m N 2)
				y(N )
Для получения оценок неизвестных параметров воспользуемся мето-
дом наименьших квадратов.
Тогда из (4.80) непосредственно имеем
	θ(n d N 1) C(n d N)ψT (n d N)Y (n d N),									(4.83)
где
								1	,	(4.84)
			C(n d N ) ψT (n d N )ψ(n d N )

при условии, что N 2n .

Выражение (4.83) может быть реализовано после того, как сформирован массив, содержащий все измерения вариаций входных и выходных сигналов.

Процедура (4.83) аналогична процедуре (4.16) для статических моде-

лей.

Рекуррентный метод наименьших квадратов (РМНК).
Результаты эксперимента (4.83) можно обработать также РМНК
θ(k) θ(k ) (k) y(k) T (k) θ(k ) ,	k , ,... (4.85)

где вектор коррекции

198

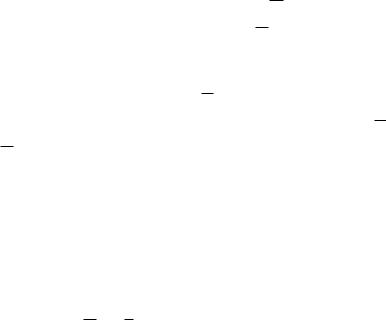
(k)	C(k ) (k)
		,	(4.86)
	T (k)C(k ) (k)
а ковариационная матрица оценок параметров
C(k) C(k ) (k) T (k)C(k ) .			(4.87)
В уравнении (4.85) выражение в квадратной скобке равно невязке меж-
ду измеренным на объекте значением выходной переменной y(k)			и предска-

занной по модели с оценками, полученными на предыдущем такте вычислений

		= − ( ) ,	(4.88)
где
		(k) T (k) θ(k ) .	(4.89)
Исходными данными для алгоритма служат
		θ(0) 0;C(0) αI n m (n m)	(4.90)
причем число α должно быть достаточно велико.
Полученные оценки (4.85) будут несмещенными θ( )			= θ при ко-
нечном	N и состоятельны в среднем квадратичном lim→∞ θ( ) = θ,
lim→∞		θ − θ θ( − θ) = 0, если выполняются следующие усло-

вия [21]:

-порядок объекта n и величина запаздывания d известны (структурная адекватность);

-измерение входного сигнала u(k) U (k) U – производятся без оши-

бок, и известно установившееся значение входа U ;

-входной сигнал представляет собой возбуждающий процесс порядка не ниже n;

-на выходной сигнал x(k) X (k) X может действовать возмущение в

виде стационарного шума V (k) . Установившееся значение X известно и

равно величине U , умноженной на статический коэффициент усиления объекта;

-невязка e(k) не коррелированна с элементами вектора данных T (k) ;

-M e(k) .

При этом сходимость оценок зависит от выбора исходных значений

C( ) и θ(0).

Для получения вариации u(k) и y(k) необходимо либо иметь оценки

установившихся значений U и Y , либо перестроить алгоритм оценивания.

Использование разностей.

Так для получения вариаций в отсутствие информации об установившихся значениях переменных переходят к разностям

199

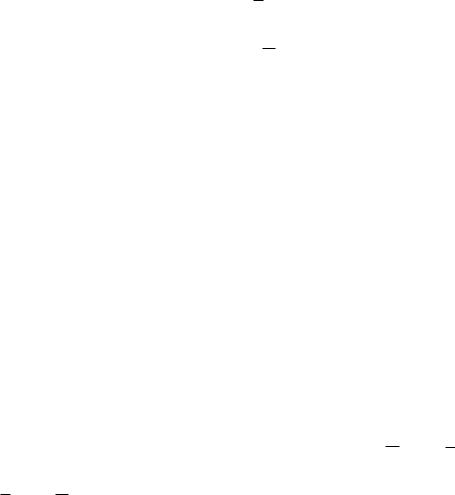
U (k) U (k ) u(k) u(k ) u(k)

(4.91)

.

Y (k) Y (k ) y(k) y(k ) y(k)

В процедуре (4.85) используют разности (4.91).

Текущее усреднение.

Другой подход состоит в оценке текущего среднего значения [21]

(k ) Y (k) Y

(k ) ,

Y

(k) Y

(4.92)

k

(k ) U (k) U

(k ) ,

U

(k) U

(4.93)

k

и переход к вариациям по формулам

(k) .

u(k) U (k) U

(4.94)

(k)

y(k) Y (k) Y

Оценивание свободного члена.

Третий подход связан с введением постоянной составляющей (константы), являющейся совместной оценкой установившихся уровней. Так, если разности (4.76) подставить в уравнение (4.75), то после преобразований имеем

X (k) a1 X (k 1) ... an X (k n) b1U (k d 1) ... bmU (k d m) q ,

						(4.95)
где константа
q 1 a1 ... an		b1	... bm		.
	X			U		(4.96)
Если расширить вектор (k ) константой			q , а вектор данных T (k)

составляющей Y , то можно в процедуре (4.85) использовать непосредственные измерения Y (k) и U (k) .

При этом будем получать и оценку . Если априори известно U или Y , то по (4.88) при известном (оцененном) легко вычислить другое установившееся значение Y или U .

Пример 4.2. Модель апериодического звена первого порядка описывается уравнениями размерности n 1, d 5, m 0

x(k) axk 1 buk 1 d – уравнение состояния;

y(k) xk Vk – уравнение наблюдения.

Здесь Vk – дискретный гауссовский белый шум с параметрами

M Vk , D Vk v ;

U k – дискретный гауссовский процесс с параметрами

M Uk , D Uk u .

Поскольку входной сигнал представляет собой центрированный процесс, т.е. вариацию относительно нуля, то и выходной процесс представляет

200

собой вариацию относительно нуля.

Для оценки неизвестных параметров a и b обычным МНК сформируем матрицы наблюдений (см. формулы (4.81), (4.82)

	y(d )
	y(d 1)
ψ	y(d 2)

y(d N )

u(0)

u(1) u(2) ,

u(N )

	y(d 1)
	y(d 2)
Y	y(d 3)	.

y(1 d N )

Вектор неизвестных параметров соответственно

a .

b

МНК-оценки по результатам наблюдений

СT

θC T Y .

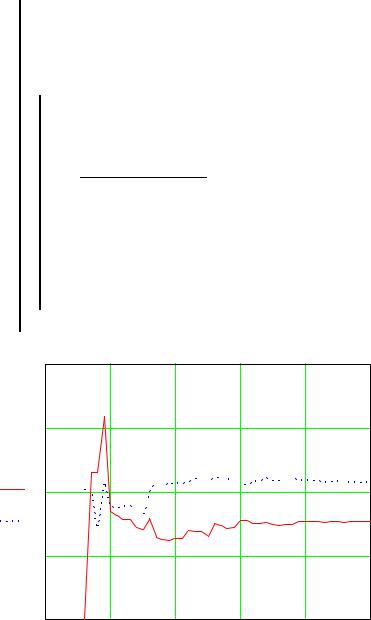
Всистеме Mathcad имитация объекта идентификации и обработка результатов эксперимента обычным и рекуррентным МНК выглядит следующим образом (рис. 4.5.).

Имитация объекта иден тификации. Порядок знаменателя n=1, запаздывание d=5, порядок чис лителя m=0

d 5

N 50

k1 5

T 5

T0 0.25 T

v 0.5

v rnorm N 1

d 0v

mu 0

u rnorm N d 1 mu 1

T0

a

k 0 d

xk 0

a e

T

b (1 a)

k1

a 0.779

b 1.106

T

b

k d 1 N d

xk a xk 1 b uk 1 d

y

k

x v

k

k

Процедура обычного М НК

		for k d 1 N d
			k 0 yk 1
			k 1 uk 1 d

C T 1

		4.789	3	6.993	4
C			10		10
			10 4
	6.993			0.018

Рис. 4.5. Пример идентификации динамического объекта в системе Mathcad

201

1 C T y															0.75		0.779
														1		T
															1.072		1.106
Процедура РМНК
	1		0					10
	0		1				10
			d		0
					0
			Cd
			for k d 1 N d
							y	k 1
			k
					uk 1 d
			k						Ck 1 k
									T		Ck 1
					1				k					k
			C		C					k			T	C
				k		k 1							k	k 1
			e	k	y	k	T					k 1
									k
			k k 1 k ek
			2
			1.5																		0.75
																		N d
	k																				1.072
			0
	k		1
			1
																				0.779
																	T
			0.5																	1.106
			00					10						20	30	40	50
															k
														Рис. 4.5. Продолжение

202