Равномерный закон распределения

Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке [a; b], если ее плотность вероятности (х) постоянна на этом отрезке и равна нулю вне его.

Плотность вероятности и функция распределения равномерно распределенной случайной величины имеют вид:

Числовые характеристики равномерно-распределенной случайной величины:

Случайная величина Х равномерно распределенная на отрезке [0; 1] называется случайным числом от 0 до 1.

Нормальный закон распределения

Непрерывная случайная величина Х имеет нормальный закон распределения, с параметрами a и , если ее плотность вероятности имеет вид:

Обозначение:

Если , то .

Функция распределения нормально распределенной случайной величины имеет вид:

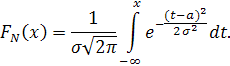
Нормальное распределение с параметрами называется стандартным: .

Если , то .

Вероятность попадания нормально распределенной случайной величины на заданный участок:

4.2 Решение типовых задач.

Классическое определение вероятности.

Применение комбинаторики к вычислению вероятностей

Пример 1. Брошены две игральные кости. Какова вероятность того, что на них выпали грани с одинаковым числом очков?

Каждому из шести исходов при броске первой кости соответствует шесть исходов, получающихся при броске второй кости, значит, всего получится 36 элементарных исходов (1-1, 1-2, ..., 1-6, 2 - 1, ... , 6 - 6). Искомому событию благоприятствуют 6 исходов из 36 (1-1, 2-2, ... , 6-6), поэтому вероятность данного события А

.

Пример 2. В урне 10 белых и 12 черных шаров, вынимают 3 из них. Какова вероятность того, что среди них ровно 2 черных?

Общее число элементарных исходов - это число способов, которым можно вынуть 3 шара из 22. Оно равно числу сочетаний из 22 элементов по 3.

n =

(первый шар выбирается 22 способами, после того, как первый выбран, второй - 21 способом, а для третьего после выбора первых двух остается 20 вариантов; однако каждый набор из трех шаров мы включили в общее число несколько раз, а именно 3·2·1=6, поэтому разных наборов из 3 шаров в 6 раз меньше, чем 22·21·20).

Общая формула для числа сочетаний из n по k приведена ниже.

Событие А, вероятность которого нужно подсчитать, состоит в том, что вынуты 2 черных и 1 белый шар.

2 черных шара из 12-ти можно извлечь

( 1-й - любой из 12-ти черных, 2-й - любой из 11-ти оставшихся, но каждый набор из двух шаров учтен дважды, поэтому 12·11 делим пополам).

1 белый шар из 10-ти можно взять

Таким образом, число благоприятствующих событию А способов равно

m =

(каждый из 66 наборов из 2 черных шаров и каждый из 10 белых шаров дают устраивающий нас вариант).

Итак,

Задание 3. Теоремы сложения и умножения вероятностей

Пример 3. В урне 5 белых и 10 черных шаров. Из урны последовательно достают два шара.

Найти вероятность того, что:

а) шары будут одинакового цвета (шары возвращают в урну);

б) шары будут разных цветов (шары не возвращают в урну);

в) хотя бы один шар будет черным (шары не возвращают в урну).

Решение

а) Событие A – шары одинакового цвета.

Рассмотрим события:

A₁ = бб – первый шар белый и второй шар белый.

Аналогично:

A₂ = чч – первый шар черный и второй шар черный.

Событие A произойдет, если достанут 2 белых или 2 черных шара:A = A₁ + A₂.

– вероятность достать второй раз белый шар не изменилась, так как шар вернули в урну.

Аналогично:

По теореме сложения вероятностей для несовместных событий A₁ и A₂:

б) Событие B – шары разных цветов.

Рассмотрим события:

B₁ = бч; B₂ = чб.

Ясно, что B = B₁ + B₂;

– первый шар в урну не вернули, поэтому вероятность вычислена при условии, что первым достали белый шар.

в) Событие C – хотя бы один шар черный.

Противоположное событие:

– оба шара белых:.

первый шар не вернули в урну, поэтому вероятность вычислили при условии, что первым достали белый шар.

Пример 4. В урне 5 белых и 10 черных шаров. Из урны последовательно достают все шары.

Найти вероятность того, что:

а) третьим по порядку будет вынут черный шар;

б) из первых трех шаров хотя бы один шар будет черный.

Решение

а) Событие A – третьим по порядку будет черный шар.

Рассмотрим события:

A₁ = ббч – первый шар белый, второй шар белый, третий шар черный.

Аналогично: A₂ = бчч; A₃ = чбч; A₄ = ччч.

Событие A произойдет, если произойдет любое из событий A₁, A₂, A₃, A₄:

A = A₁ + A₂ + A₃ + A₄.

Так как из урны последовательно достают все шары, то шары в урну не возвращают и при вычислении вероятности события A₁ = ббч рассчитываем условные вероятности того, что второй шар белый (при условии, что первый шар белый) и что третий шар черный (при условии, что первый шар белый и второй шар белый):

Аналогично:

По теореме сложения вероятностей для несовместных событий:

20/273+45/273+45/273+72/273=182/273

б) Пусть событие B – из первых трех шаров хотя бы один шар будет черным.

Противоположное событие: – все три шара белые:.

Пример 5. В урне 5 белых, 10 черных и 5 красных шаров. Три из них вынимают наугад. Найти вероятность того, что по крайней мере два из них будут одноцветными. Шары в урну не возвращают.

Решение

Событие A – по крайней мере два шара одноцветные.

Противоположное событие:

– все шара разного цвета.

Рассмотрим события:

A₁ = бчк – первый шар белый, второй шар черный, третий шар красный.

Аналогично:

A₂ = бкч; A₃ = чбк; A₄ = чкб; A₅ = кбч; A₆ = кчб.

Событие A произойдет, если произойдет любое из событий A₁, A₂, A₃, A₄, A₅, A₆:

A = A₁ + A₂ + A₃ + A₄ + A₅ + A₆.

Так как шары в урну не возвращают, то при вычислении вероятности события A₁ = бчк рассчитываем условные вероятности того, что второй шар черный (при условии, что первый шар белый) и что третий шар красный (при условии, что первый шар белый и второй шар черный):

Аналогично:

По теореме сложения вероятностей для несовместных событий: