3. Наблюдаемость динамических систем. Соотношение двойственности.

При синтезе оптимальных систем управление является функцией состояния системы, а не ее выхода.

Выход - координаты системы, которые поддаются измерению, следовательно, размерность вектора будет меньше, чем размерность вектора .

При реализации оптимальных законов управления встает задача, как по вектору оценить . Это задача наблюдения. Условие существования ее решения – наблюдаемость системы.

Состояние наблюдаемо в момент времени , если для заданного управления , такое, что знание управления на интервале и выхода достаточно для определения .

Если каждое состояние наблюдаемо при , то говорят, что система наблюдаема в .

Если каждое состояние наблюдаемо в любой момент времени , то говорят, что система (полностью) наблюдаема.

Понятия управляемости и наблюдаемости являются внутренними свойствами системы, то есть они сохраняются при всех эквивалентных преобразованиях системы.

(1)

u(t), y(t) – функции входа и наблюдаемого выхода системы. А,В,С – известные матрицы.

Наряду с исходной системой рассмотрим сопряженную к ней систему:

(2)

Определим производную от векторов состояния исходной и сопряженной системы.

Проинтегрируем это выражение

Принимаем и учитывая (1), получим:

(3)

Если известно , то данное выражение можно считать операцией оценки, которое позволяет оценить , если известны y, u.

Вектор выбирается в зависимости от того, какая из переменных состояния оценивается.

Если нужно оценить , то i-я компонента принимается = 1, остальные = 0.

Если сопряженная система управляема, то должна существовать функция входа под действием которой данная система переходит из исходного состояния в 0 за время .

Пусть - функция входа, которая решает данную задачу, тогда состояние определяется из соотношения (3).

(4)

Следовательно, анализ наблюдаемости динамических систем свелся к задаче управляемости сопряженной системы.

Данная взаимосвязь между управляемостью и наблюдаемостью линейных динамических систем называется соотношением двойственности.

Соотношение двойственности указывает на то, что исходная система (1) наблюдаема, если сопряженная к ней система (2) управляема.

Управляемость сопряженной системы имеет место, если выполняется следующее условие:

4. Оценка вектора состояния линейной динамической системы. Наблюдатель Люенбергера.

Решение задачи ОУ приводит к закону управления, который является функцией переменных состояния, следовательно, при решении этих задач полагается, что вектор состояния полностью известен, однако в реальных системах это условие как правило не выполняется.

Чаще всего приходится сталкиваться с ситуацией, когда измерению поддаются сигналы, образующие вектор измерения y(t), составляющие которого являются известными функциями состояния системы.

Устройство, восстанавливающее вектор состояния по измеряемым координатам называется наблюдателем.

Система n-го порядка: (1) 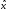- вектор оценки

Состояние системы является наблюдателем полного порядка для системы вида (2) (2)

При имеем (совпадение вектора оценки и состояния) для всех ; Будем рассматривать наблюдатель, у которого F, G и H определяются следующим образом:

(3) - матрица коэффициентов усиления наблюдателя (n x m).

Подставим (3) в (1): (4) (5)

оценка вектора наблюд.

Структурная схема наблюдателя:

K_H

+

B(t)

C(t)

+

A

Наблюдатель- это устройство, позволяющее по управлению и измеряемым координатам оценить вектор состояния системы.

Докажем, что система вида (5) есть система для оценки вектора состояния.

Пусть S(t)- решения сопряженного уравнения, удовлетворяющего краевым условиям, при которых соотношение является операцией оценки. ( )

Из теории решения 2-х точеных задач известно, что v(t) является функцией состояния сопряженной системы.

или (6)

Система (6) является сопряженной для системы (4)

проинтегрируем

то есть вектор оценки совпадает с вектором состояния в момент

Следовательно, система вида (4, 5) есть система для оценки состояния.

Введем в рассмотрение вектор оценки (вектор ошибки оценки)

Ошибка оценки удовлетворяет следующему диф.уравнению:

(7)

Решение этого уравнения имеет вид: (8)

Если вектор оценки совпадает с вектором состояния в момент , то вектор ошибки для .

В реальных системах из-за действия возмущений и шумов 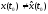, поэтому матрицу выбирают таким образом, чтобы ошибка наблюдения при . т.е. система вида (7) должна быть асимптотически устойчивой.

Для системы с постоянными параметрами асимптотическая устойчивость наблюдателя определяется собственными значениями матрицы . Назовем их полюсами наблюдателя. Для устойчивости наблюдателя необходимо и достаточно, чтобы полюса наблюдателя находились в левой полуплоскости.

Наблюдатель рассматриваемого вида для системы с постоянными параметрами называется наблюдателем Люенбергера.

Для быстрой сходимости ошибки к 0 необходимо выбрать таким образом, чтобы полюса наблюдателя были удалены как можно больше влево от мнимой оси корневой плоскости.

Решение уравнений (7) помимо вида (8) может быть представлено следующим образом: - матрицы правого и левого собственных векторов.

- отрицательные полюса наблюдателя.

Чем больше по модулю будут полюса наблюдателя, тем ближе к нулевой будет матрица и меньше . Однако значительное удаление от мнимой оси влево в большинстве случаев может быть достигнуто путем выбора больших значений коэффициентов матрицы усиления, что, в свою очередь, делает наблюдатель весьма чувствительным к шумам измерения. Задача определения матрицы коэффициентов усиления , обеспечивающей наилучшие характеристики процесса восстановления в условиях действия шумов называется задачей оптимальной фильтрации.