2.4.3. Импульсная функция и импульсная характеристика
Введем функцию, определяющую прямоугольный импульс длительностью Δt, высотой 1/ Δt и площадью S = 1 (рис. 49).
Рис. 49
Такой импульс получается из двух единичных функций, смещенных одна относительно другой на длительность импульса:
Наибольший интерес представляет предельный случай прямоугольного импульса, когда его длительность стремится к нулю (Δt → 0), а высота – к бесконечности (A = 1/Δt → ∞):
Эта функция называется импульсной функцией и обозначается δ(t). Её часто называют также дельта-функцией или функцией Дирака. Импульсная функция обладает следующими свойствами:
1) равна нулю при t < 0 и t > 0, т. е. δ(t) = 0 при t ≠ 0;
2) бесконечно велика в точке t = 0: δ(0) = ∞,
3) кроме того
Если импульсная функция отлична от нуля не в момент t = 0, а в момент τ, т.е. запаздывает на время τ, то она записывается с запаздывающим аргументом δ (t - τ). При этом сохраняется основное свойство функции
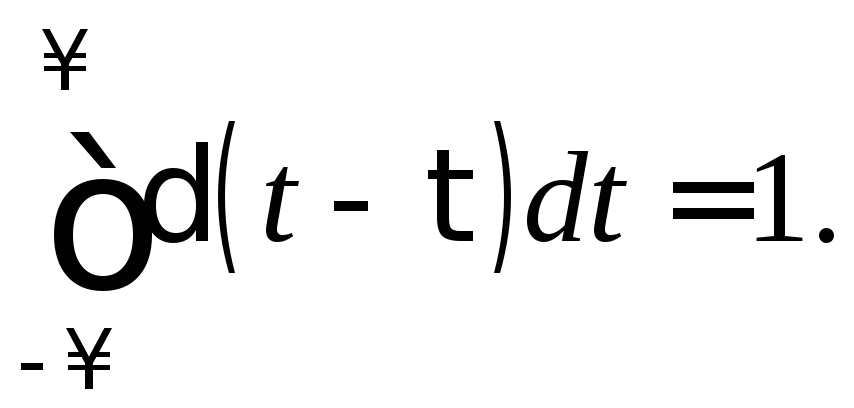
Поскольку импульсная функция получена предельным переходом от единичной функции, следовательно, она является производной от единичной функции.
.
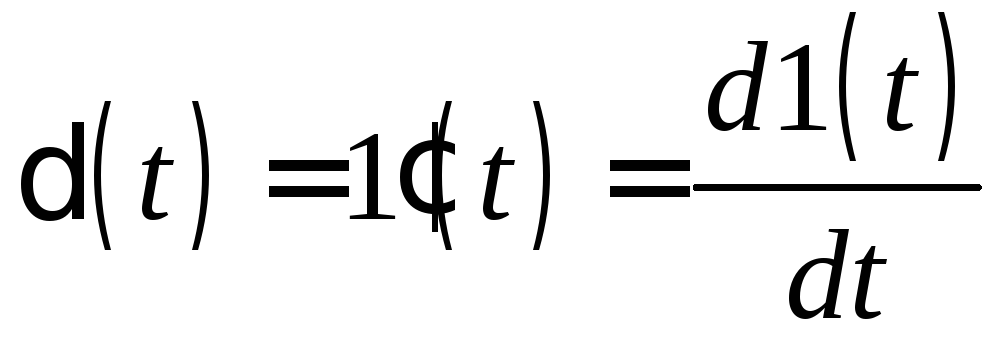Из последнего выражения следует и обратное соотношение:
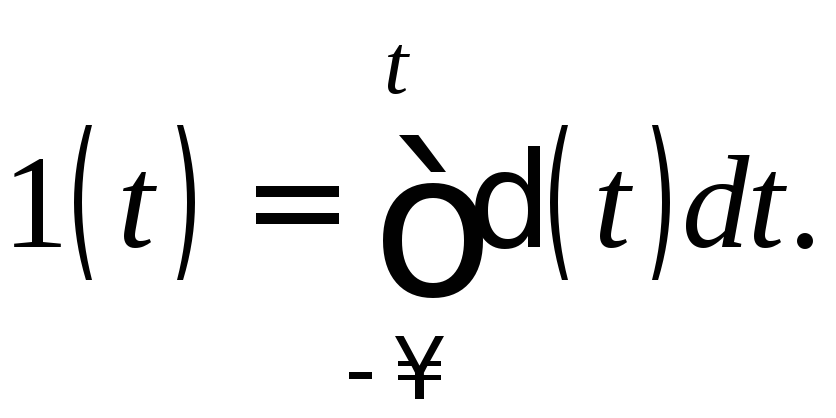
Важнейшим свойством дельта-функции является фильтрующее свойство записываемое в виде интегральных соотношений
,
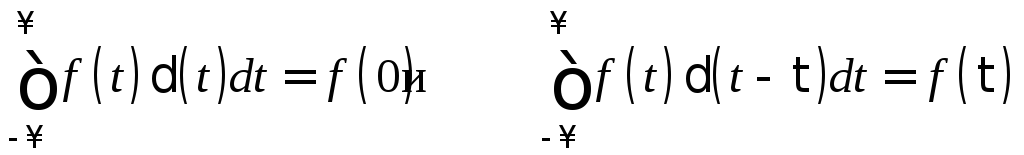где f(t) – произвольная непрерывная функция.
Подынтегральная функция в последней формуле равна нулю всюду, кроме точки t = τ.Функция f(t) в этой точке равна f(τ). Тогда f(τ) можно вынести за знак интеграла, а интеграл будет равен единице в силу свойства импульсной функции:
.
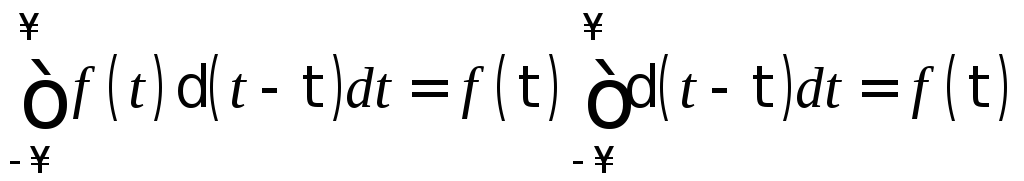Таким образом, интеграл от произведения импульсной функции и любой непрерывной функции равен значению непрерывной функции при том значении переменной интегрирования, при котором аргумент дельта-функции обращается в нуль.
Для определения отклика цепи на сложное воздействие оказывается достаточно знать отклик цепи на дельта-функцию, который называется импульсной характеристикой. Её можно определить так:
,
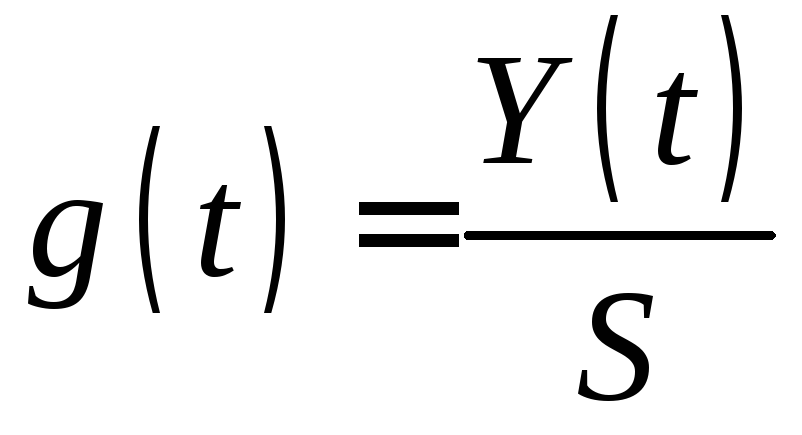где S = δ(t) – воздействие, Y (t) – отклик.
Импульсная
характеристика
.
Если воздействие увеличивается в а раз, в силу линейности во столько же раз возрастает и отклик. Если воздействие запаздывает на t1, то на такое же время запаздывает и отклик.
2.4.4. Интеграл наложения
Рассмотрим применение импульсной характеристики для расчета отклика цепи на сложное воздействие. Как и в предыдущем случае, найдем ток в цепи при воздействии входного напряжения e(t) (рис. 50).
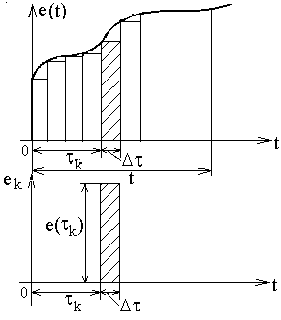
Рис. 50
Аппроксимируем e(τ) последовательностью прямоугольных импульсов en(t) малой длительности Δτ:
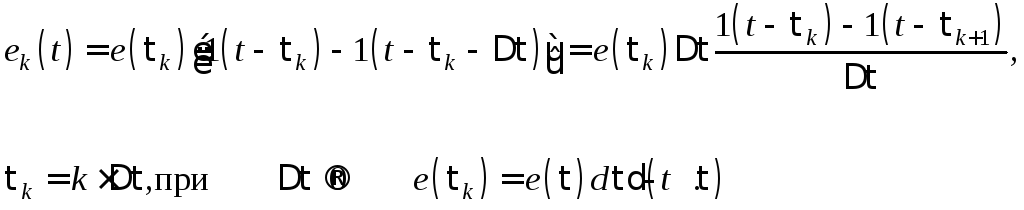
Каждый отдельный прямоугольный (элементарный) импульс с площадью e(τ) dτ δ(t – τ) вызовет ответный отклик в виде составляющей тока
dik(t) = e(τ)g(t – τ)dτ,
где g(t – τ) – значение импульсной характеристики в момент наблюдения t при воздействии импульса на цепь в момент τ.
Результирующий отклик на всё воздействие получим, используя принцип наложения, суммируя бесконечно малые составляющие di(t), вызванные последовательностью бесконечно малых по длительности прямоугольных импульсов напряжения:
.
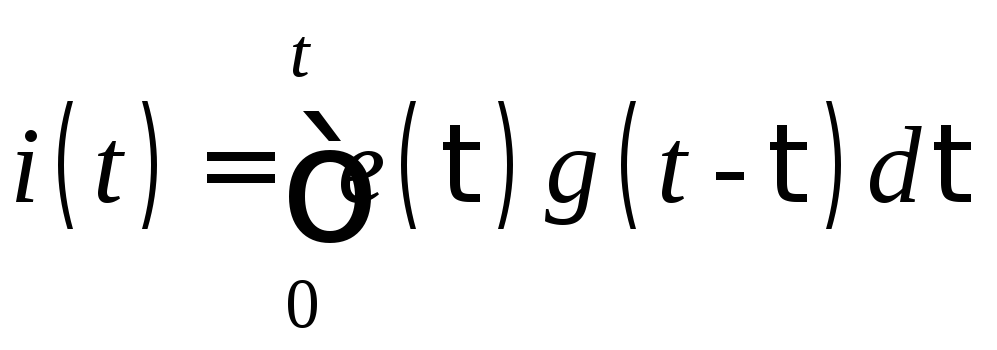Полученный интеграл называется интегралом наложения. Используя теорему свертки, получим ещё одну форму интеграла наложения
.
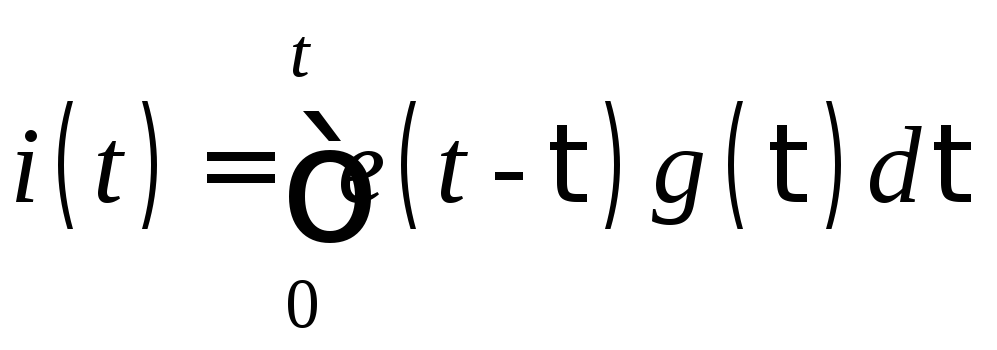